技术背景
这里借用一个网友的例子:预测单词的词性
问题
首先给定一个句子:我爱吃苹果,目的是为了预测每一个单词的词性。
解决方案一
为了让机器学习来帮助我们解决问题,最首要的就是要准备数据来训练我们的算法模型,在本次例子中,要预测单词的词性,直觉理解中,输入就是单词,输出就是单词的词性。
?这样将数据送入到模型中让模型学习,最后就可以实现预测作用。
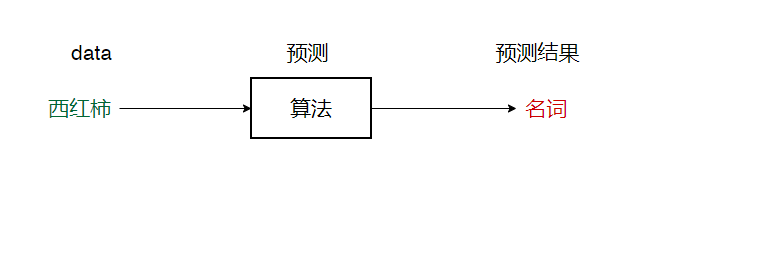
特点:如果将我爱吃西红柿这一句话看作是有时间顺序的。那么对于这类传统的算法模型来说,一次只输入一个时刻的数据,然后就可以得到预测结果。
解决方案二
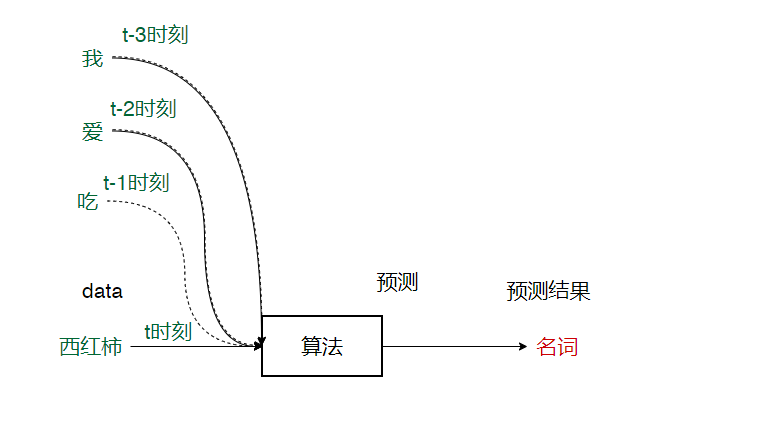
?在方案一提到我爱吃西红柿这一句话是有时间顺序的,为什么呢?是因为他的这一时刻是结果会受到前几个时刻的影响,比如我们在预测西红柿的词性时:
我是名词
爱是形容词
吃是动词
最后在预测是西红柿的词性的时候,由于前面出现过名词和动词,那么后面出现的大概率是形容词。从这里可以看出,对于这一类具有时序性的数据中,如果利用好前面时刻的数据,那么将更合理且更加有利于结果的预测。
注:以上对于t-1和t-2以及t-3这几个时刻并不是表示直接输入到模型中,而是便于表达,便于说明对于t时刻的预测结果是受到前几个时刻的影响,至于是如何影响?等RNN的时候会详细说。
?这也就是时序性问题,这样的场景还很多,诸如:
- ai翻译:此刻的翻译预测结果,必将受到前几个时刻的影响
- ai写诗:当下这个词的生成预测,一定受到前几个时刻的影响。
- 商品购买预测:一个人购买的产品可能是有顺序的,比如,一个人买了床单、被罩、后面可能会买枕头。这也是时序问题。
显然对于这一类问题,将其看作时序性问题是最合理的,这也就是RNN诞生的理由。用于解决时序性问题。
RNN
RNN命名(废话开篇)
?首先网上一开始就开始纠结它的中文名:循环神经网络或者是递归神经网络,要我说,既然纠结不清,那就直接不纠结,就叫RNN就完事儿了,知道它是用于解决时序性问题就行了。
时序问题的直觉解决方案
前面的方案二中已经稍微讲解了一点,RNN是用于解决时序问题的,时序问题就是说当下这一时刻t的预测输出不仅与t时刻的输入有关,还与前几个时刻有关系。
依旧是以我爱吃苹果的词性预测为例。
预测词性
- 预测我:我----->名词
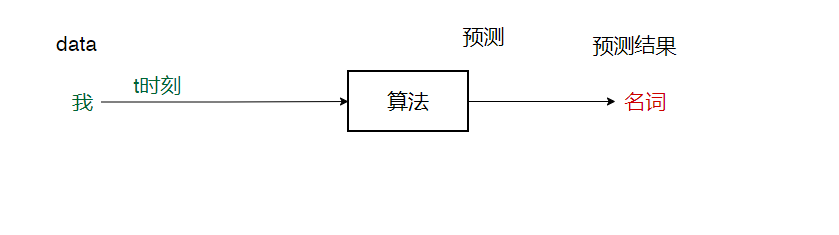
- 预测爱:爱----->形容词
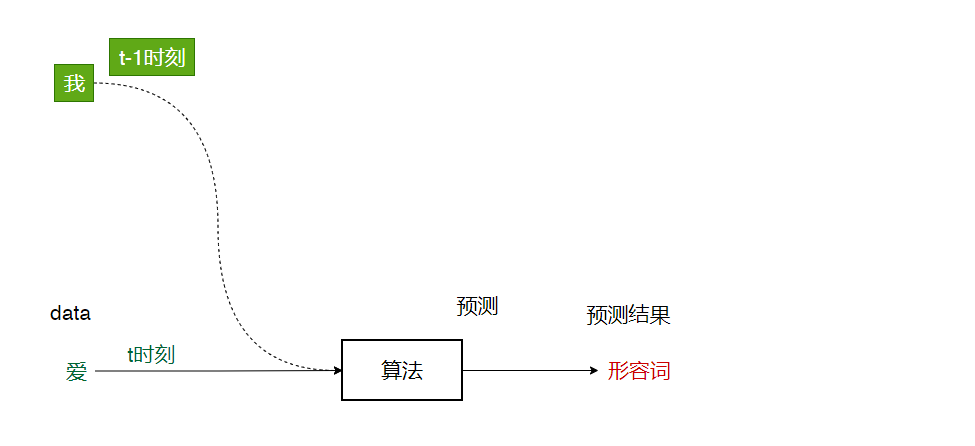
- 预测吃:吃----->动词
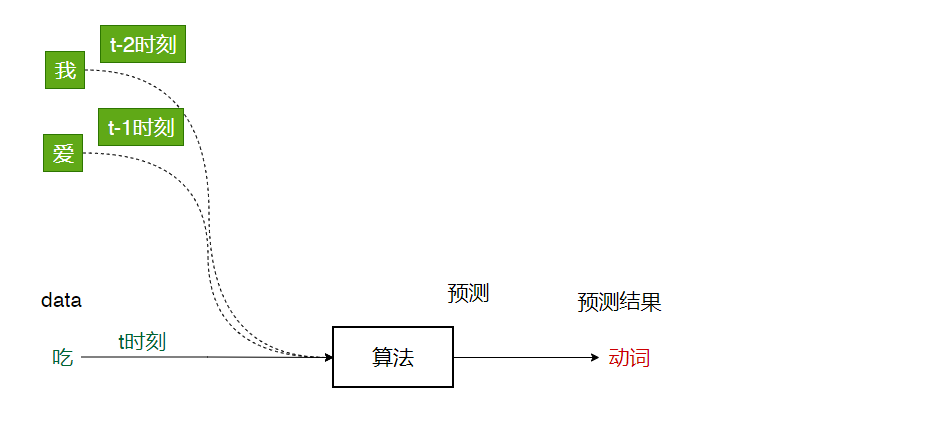
- 预测西红柿:西红柿----->名词
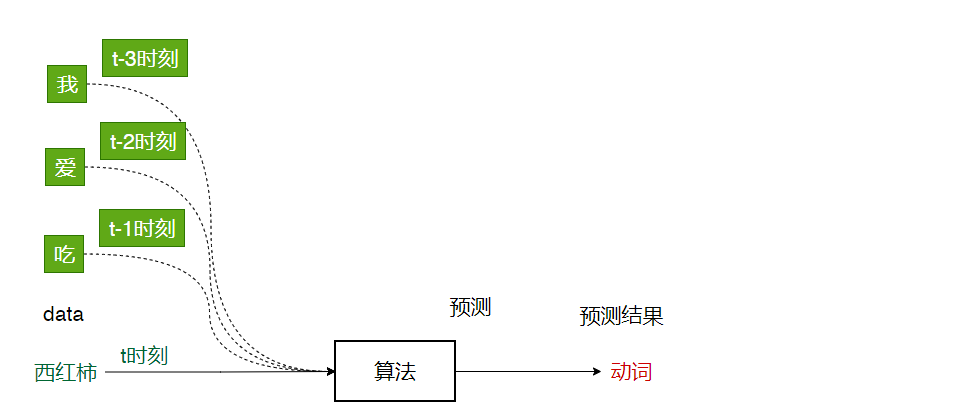
RNN的引出
??以上就是我最开始对时序问题的直觉的解决方案:t时刻的预测结果考虑到了t时刻之前多个时刻的输入。这个思路是完全没问题的,但是实现上是有问题的。
在机器学习甚至任何算法中,通常我们最应该保证的一点就是:算法入口的输入数据的维度应该保持固定,比如这个算法一次输入的数据是两个,那么它就自始至终应该都是2,回看我们上面的图中可以看出,我们虽然考虑到前几个时刻的数据输入,但是每一次输入的数据维度不一样,那么该如何解决呢?
为了便于理解,你可以理解为在RNN算法中,引入了记忆单元,选择将前k个时刻(k由自己认为固定)的数据记下来,然后输入的数据只有1个,就是当前t时刻的数据。下面引入李宏毅老师最经典的ppt来说明这个记忆单元是如何实现的。
李宏毅老师的例子引出RNN的记忆单元
首先举一个两输入的的预测模型。
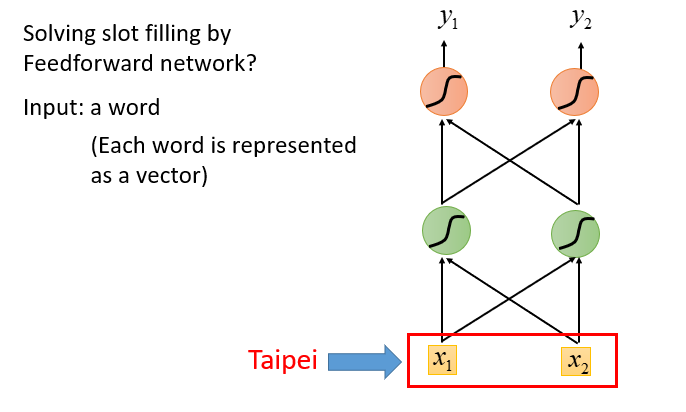
这里忽略掉x1和x2到底是什么,你只需知道这是一个传统的两输入两输出的的神经网络,它没有记忆单元,那么在RNN中是如何引入记忆单元的呢?其实很简单,看下图
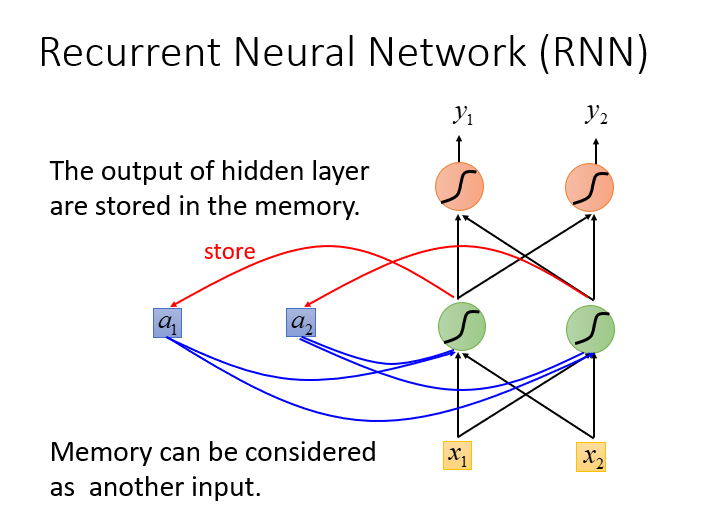
下图中的a1和a2就是RNN的精髓:记忆单元,现在我们就可以根据我们最开始的理解中得到:输入是固定的2维数据,在输入到网络中之后再与记忆单元进行加权运算。下面是李宏毅老师的例子
输入模型中的数据依次是[1,1],[1,1],[2,2]
记忆单元初始化为[0,0]
注:为了方便推演和讲解,将所有的权重假设为1,将激活函数为y = x
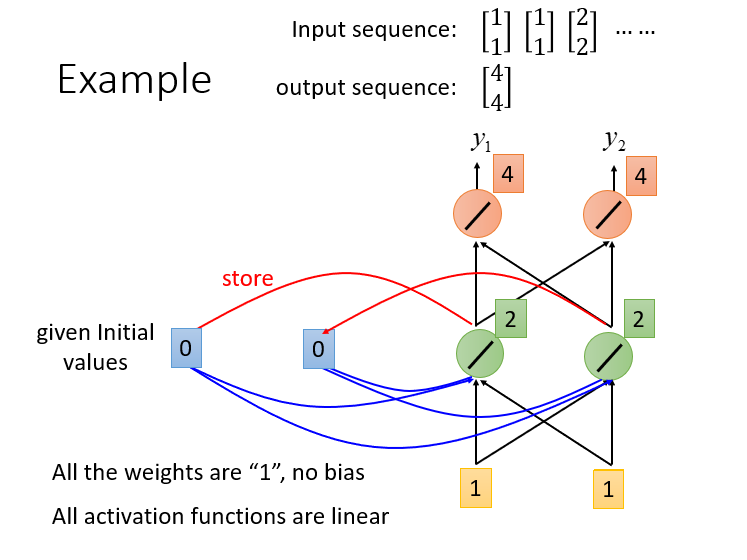
- 当输入[1,1]时,经过绿色的神经元运算后,得到[2,2],然后再与记忆单元的[0,0]进行加权得[2,2],最后经过最后一层神经元计算输出结果为[4,4],同时隐藏节点的[2,2]将被放入到记忆单元进行存储。
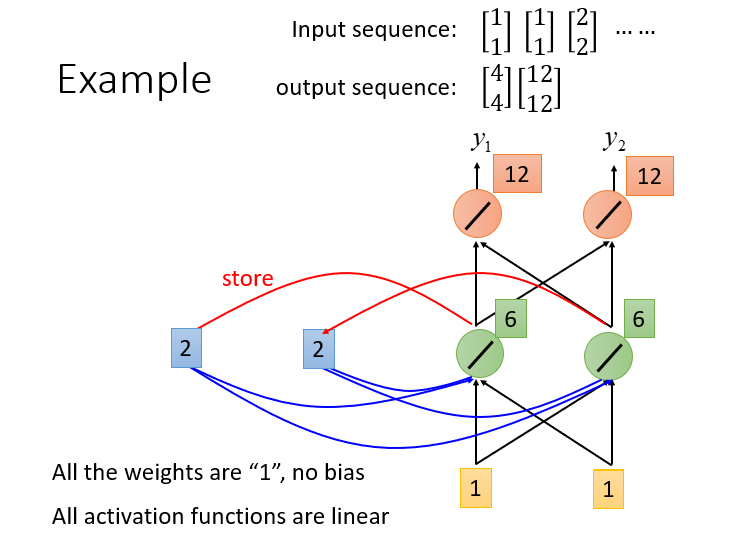
2. 接下来输入[1,1],此时经过绿色神经元运算后同样和上一次一样得到[2,2],这时在于上一次保留再记忆单元中的数据进行加权,将得到[6,6],最后经过最后的神经元计算得到输出为[12,12]。
其实例子举到这里就大致清楚了。
1.两次输入都是[1,1],但是输出结果完全不一样,这就表明考虑时序问题的RNN和普通网络是不一样的。
2.在每一次的计算中,都是将输入与记忆单元进行加权,然后一方面进行结果输出计算,另一方面有将加权和重新保存入记忆单元供下一次使用,这表明记忆单元记载着本时刻之前是所有时刻的信息。
3.记忆单元的个数与隐藏层的个数是相等的。
现在RNN的工作流程就大致清楚了,原先为了方便推演,将所有权重进行假设为1,将激活函数设置为y = x,现在推广到一般问题上,权重为W,激活函数为
δ
(
x
)
\delta (x)
δ(x)。
首先强调下图中左右都是同一个网络,只是左图表示的是t时刻输入,右图表示t+1时刻输入。
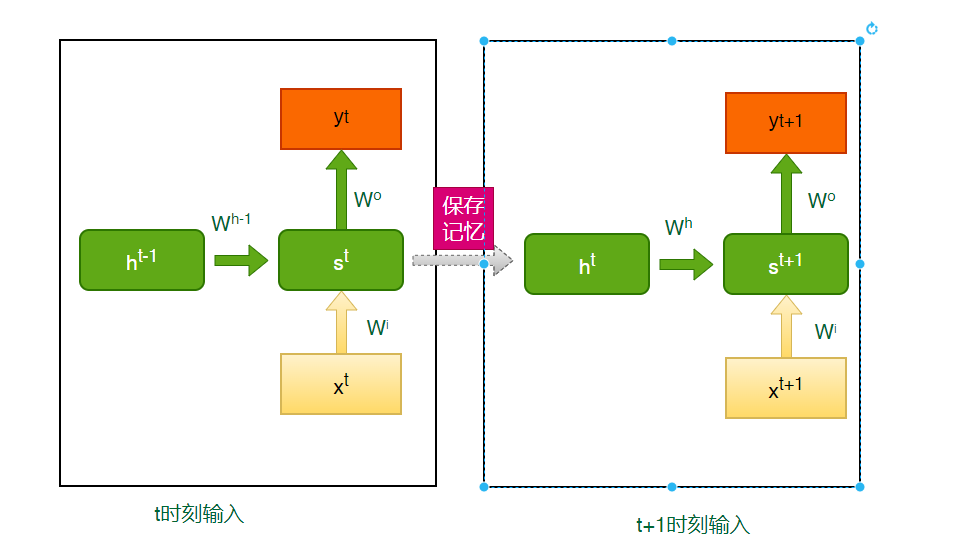
1.t时刻,隐藏层结果等于此时刻输入乘以一个权重与上一个时刻保留的记忆数据乘以权重的加和,
S t = δ ( X t × W i + h t ? 1 × W h ? 1 ) S^{t} = \delta (X^{t} \times W^{i}+ h^{t-1} \times W^{h-1} ) St=δ(Xt×Wi+ht?1×Wh?1)
2.隐藏层的结果一份保留到了记忆单元
h t = S t h^{t} = S^{t} ht=St
3.隐藏层结果乘以输出权重得到输出结果
y t = δ ( S t × W o ) y^{t} = \delta (S^{t} \times W^{o}) yt=δ(St×Wo)
至此t时刻的一次的算法流程就完成,接下来就是不断在不同时刻循环这个过程而已。
以上就是关于RNN的原理,下面再来看看网络上的一些流行的图,首先第一张:
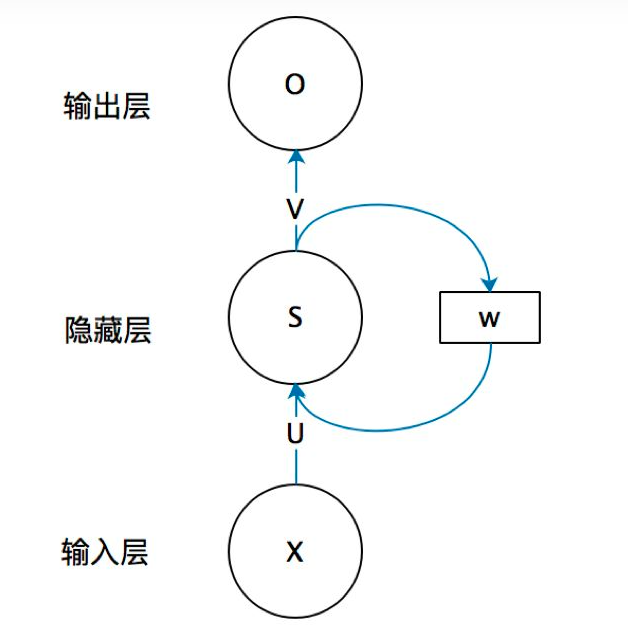
这个图就是上面那个图的折叠,我们把这个图展开:
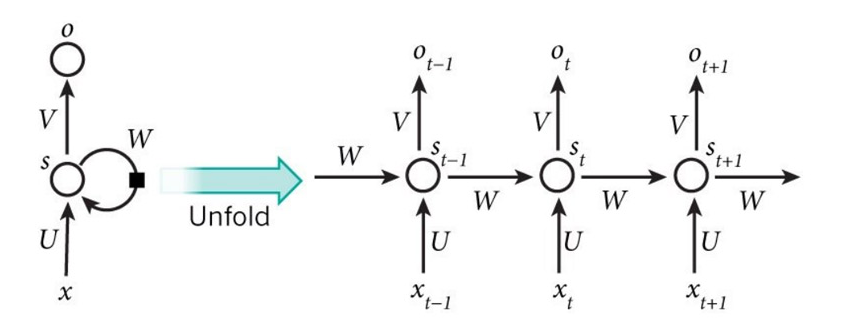
展开后的右图就是我上面根据李宏毅老师画出的彩色图,所以左图中最难理解的这个环也就明白了
计算本时刻的输出时,它将利用上一时刻的记忆
S
t
?
1
S_{t-1}
St?1?,先计算出
S
t
S_{t}
St?,然后接着计算出输出
O
t
O_{t}
Ot?。最后还将
S
t
S_{t}
St?保存入记忆单元,提供下一次使用。
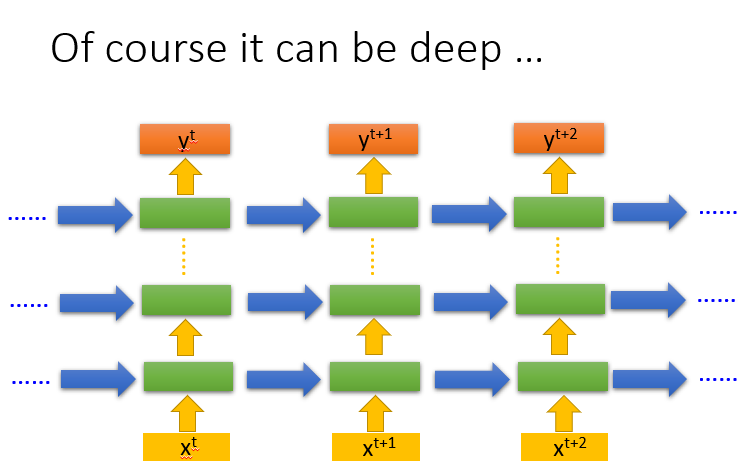
当然以上只是讲了一层隐藏层下的RNN,如果是多层RNN,每一层就会有记忆单元,,他表示同一个时刻在不同网络层的记忆单元。
梯度消失
梯度消失产生的原因
在模型训练的过程中,随着深度的增加,模型的预测结果会更好,因为能学到更多深层次的东西,但是也会随着梯度的增加带来一个问题:梯度消失。梯度消失导致靠近输入层的权重无法得到很好的训练和更新,也就使得算法无法收敛。很多讲RNN时,都会从数学的角度分析梯度消失的问题,但是我认为完全没必要。
我们只要知道:随着网络的深度增加,必然带来梯度消失的问题。在RNN中,虽然很多时候网络层只要2层,但是记忆单元会记住前面所有时刻的数据,他们共享权重
W
t
W_{t}
Wt?。这将导致
W
t
W_{t}
Wt?出现多次点乘的效果,和深层神经网络是一样的。所以这也是RNN产生梯度消失的原因
梯度消失解决方案
1.更换激活函数
深层网络出现梯度消失,一部分原因是因为激活函数,如果激活函数为sigmoid,因为sigmoid的倒数最大值为0.25,这就表明,方向bp时,这个倒数越乘越小,就出现了梯度消失。所以考虑换掉sigmoid,可以换为relu,这样倒数大小为1,那么权重反向bp时,梯度不会越乘越小。
2.BatchNorm
BN操作是规范每一层的输入,这将可以控制每一层输入的平稳,也就不会因为输入过大导致梯度爆炸,也不会因为输入过小而导致梯度消失。
3.残差结构
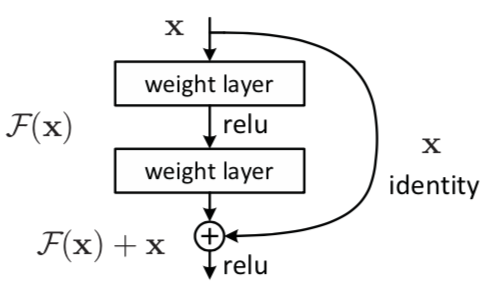
原始深度网络中,只有主干的多个层,而resnet中多了一点,就是曲线x部分,这一部分是不带权重的跨层传递到下面的网络层,当在进行反向求梯度的过程中,直接传递过来的x那部分的梯度永远是1,这将导致反向梯度不会太小,就解决了梯度消失的问题。
为了解决RNN的梯度消失难以训练的问题,就引出了LSTM,LSTM就采用了类似残差网络的思想来解决梯度消失问题。
LSTM
LSTM又叫长短期记忆网络,在RNN的基础上,每个神经元加上三个门:输入门、输出门、遗忘门
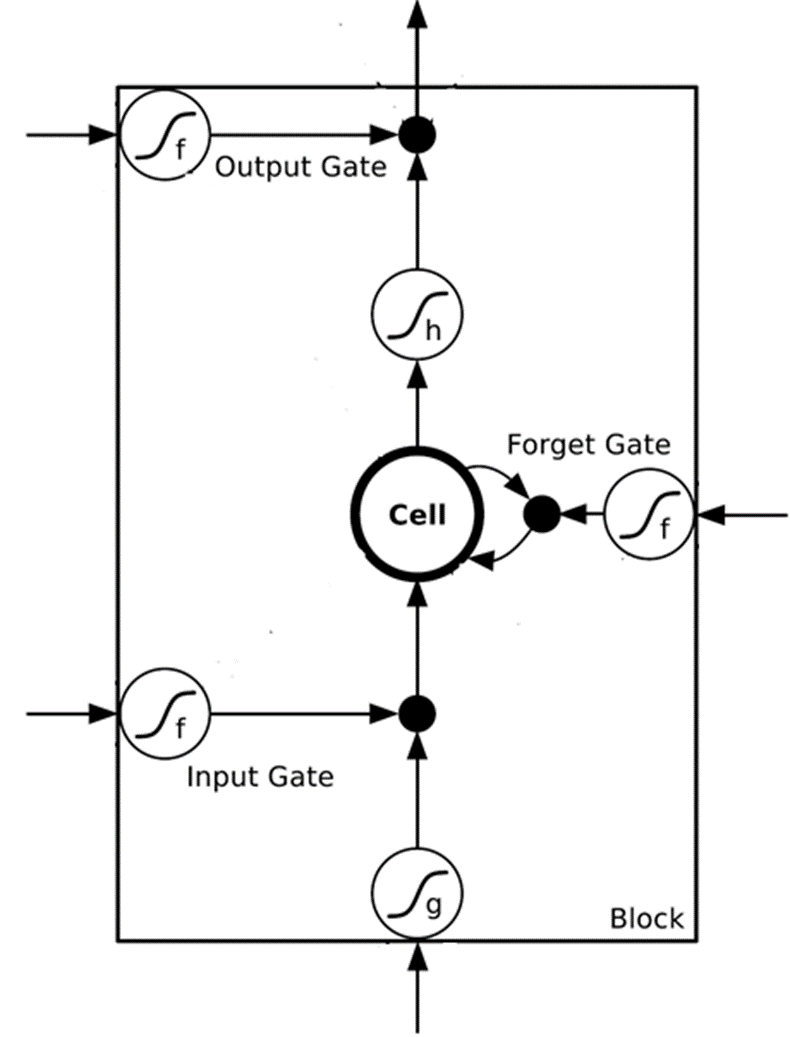
所以一开始我们举例的两输入的模型就会变成如下所示。
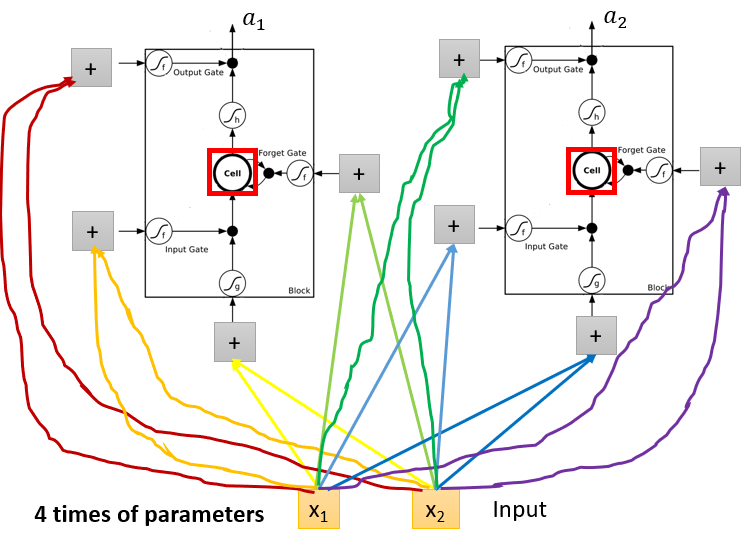
将上图整合一下,就得到以下:
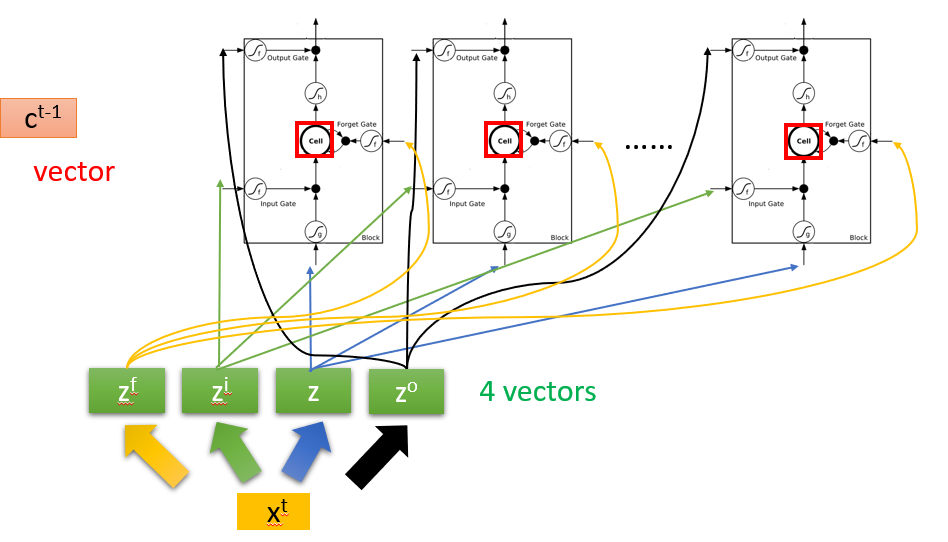
网上的大佬们为了方便观看,进一步把图片化简为:
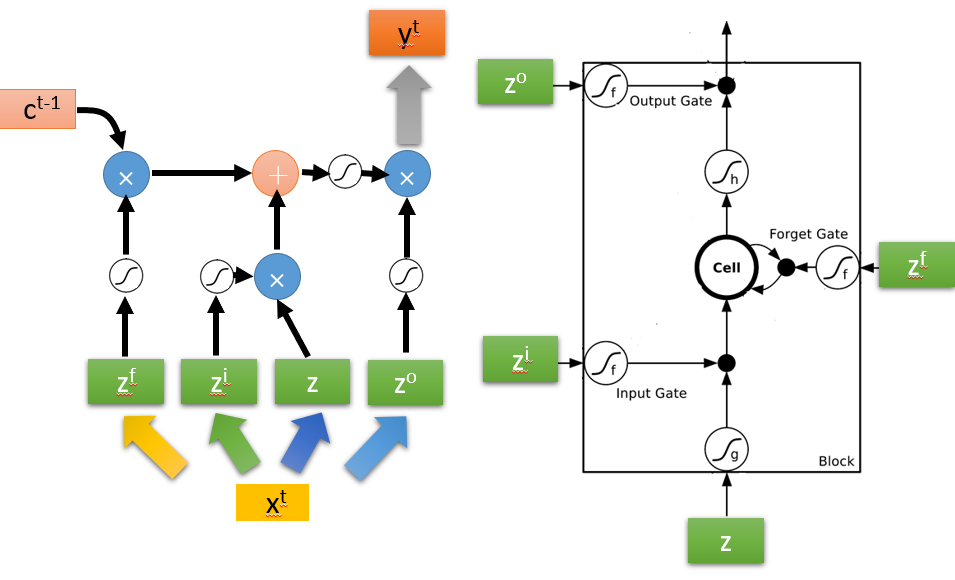
为了和右图对上,我下面做一个简单的标注,可以看出左1为遗忘门,左2为输入们,左3才是真正是输入,最右边为输出门,这样就全部对上了。
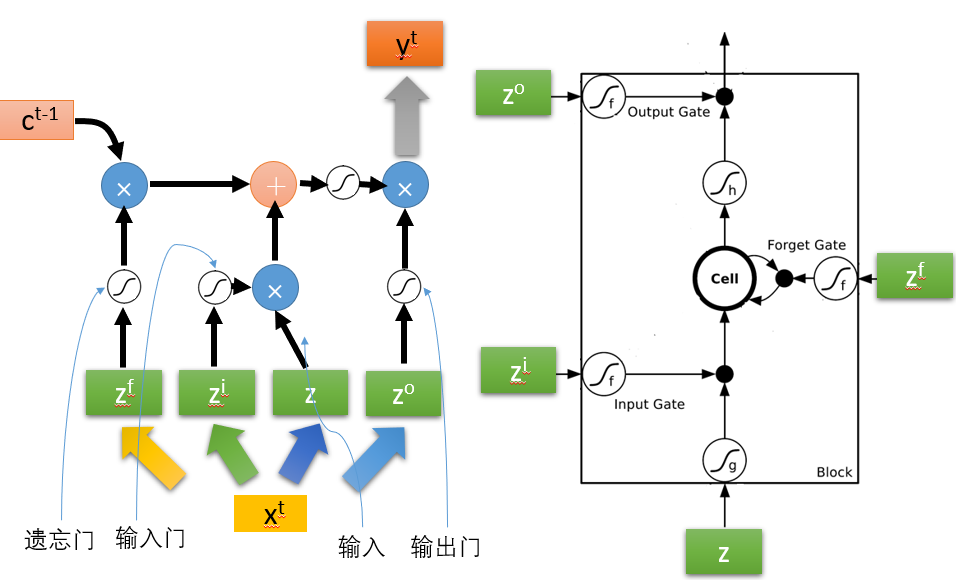
但是实际情况下,输入并不简单的是当前时刻的,而是将上一时刻的输出也加到了下一时刻的输入。
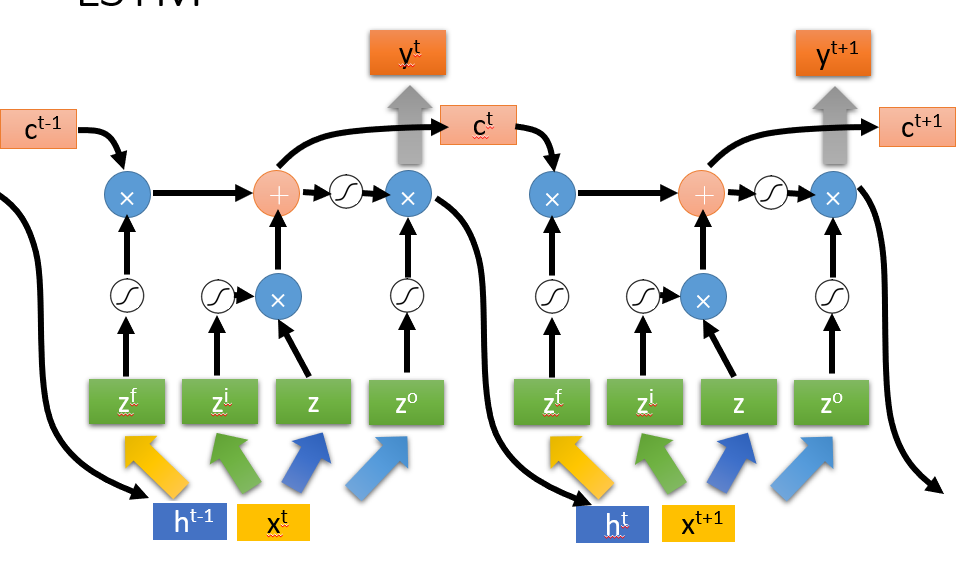
上图也等同于网上的另一个比较多的图:
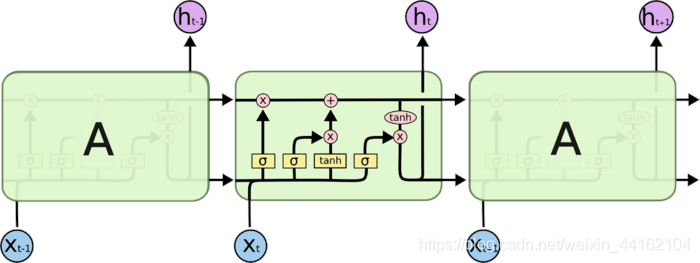
这也就是LSTM的全貌了。
LSTM如何缓解梯度消失问题
在讲解LSTM如何缓解梯度消失问题之前,我们先拆解以下LSTM
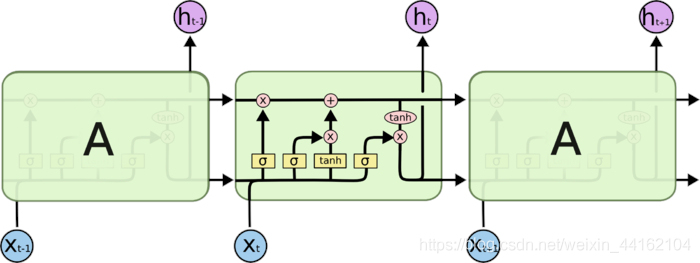
遗忘门
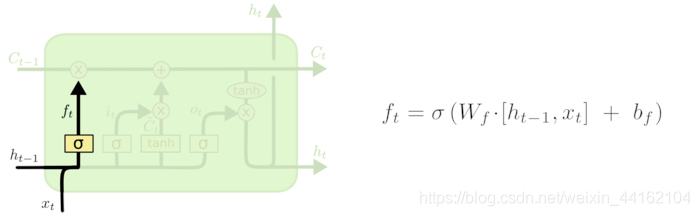
h
t
?
1
h_{t-1}
ht?1?为上一个时刻的输出
输入门与输入
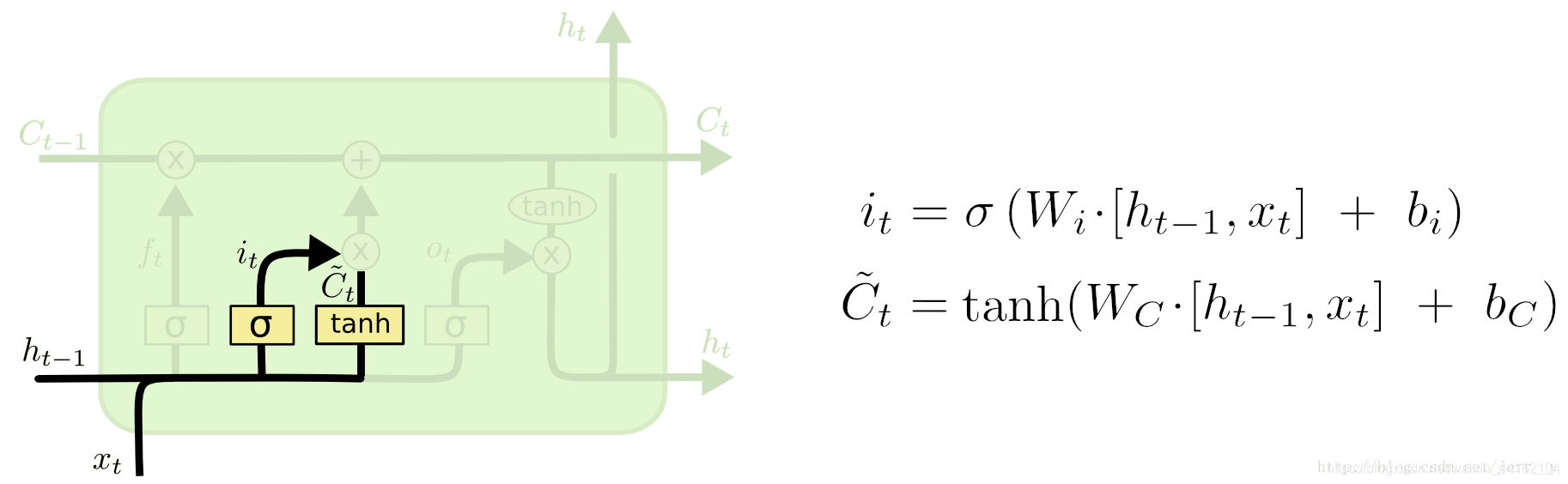
其中
i
t
i_{t}
it?为输入门,而
C
~
t
\tilde{C}_t
C~t?则为输入。
所以结合了输入、输入门、遗忘门,就可以得到,隐藏层的值为
C
t
=
f
t
⊙
C
t
?
1
+
i
t
⊙
C
~
t
C_t = f_t\odot C_{t-1} +i_t\odot \tilde{C}_t
Ct?=ft?⊙Ct?1?+it?⊙C~t?
这个值一方面会用于输出的计算,另一方面会存入到记忆单元,用于下一次输入时计算,这我们在RNN时候讲过了。
输出门
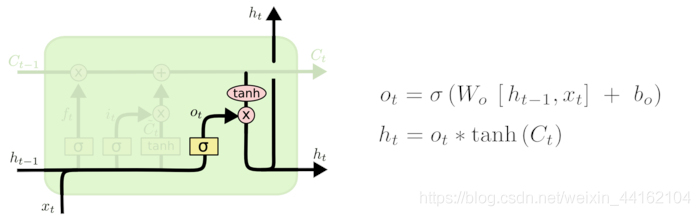
o
t
o_{t}
ot?为输出门,而
h
t
h_t
ht?则为输入,和
C
t
C_t
Ct?一样,一方面会直接输出结果,另一方面将用于下一时刻的输入。
RNN梯度消失的原因回忆
在RNN中,因为引入了记忆单元,记忆单元共享权重W,在不断的记忆和点乘中,使得记忆单元和网络的深度如出一辙,这也就引起了梯度消失的问题。那么要解决梯度消失,自然就要从记忆单元开始入手了。
梯度消失的解决办法总结
上面我们也讲过解决梯度消失的办法
- 改变激活函数,从sigmoid变为tanh或者其他;
- 引入BatchNorm;
- 引入残差结构
在LSTM中,就是在记忆单元上用了上面梯度消失的两种办法:改变激活函数为tanh和引入了类似的残差结构。
我们把记忆单元的计算公式先摆出来:
C
~
t
=
t
a
n
h
(
W
c
?
[
h
t
?
1
,
x
t
]
+
b
c
)
\tilde{C}_t = tanh(W_c\cdot \left [ h_{t-1},x_t \right ] + b_c )
C~t?=tanh(Wc??[ht?1?,xt?]+bc?)
C
t
=
f
t
⊙
C
t
?
1
+
i
t
⊙
C
~
t
C_t = f_t\odot C_{t-1} +i_t\odot \tilde{C}_t
Ct?=ft?⊙Ct?1?+it?⊙C~t?
可以看出lstm缓解梯度消失的三点:
- C t C_t Ct?的左侧,在记忆单元中,上一个记忆的值上乘以了一个遗忘门 f t f_t ft?,这就可以使得有些没有用的时刻的数据,通过 f t = 0 f_t = 0 ft?=0时,直接遗忘掉,这也就好比在深层网络中减少了网络的层树,达到了缓解梯度消失的问题。
- C t C_t Ct?的右侧,将输入乘以输入门之后,与前面所有时刻的记忆单元值进行加和,可能你会问,这和之前RNN的计算逻辑是一样的,只是多乘上了一个输入门和遗忘门而已,至于遗忘门的作用,前一点已经说了,但是后面一项的作用,是在于 C ~ t \tilde{C}_t C~t?的计算,这个计算中,妙处就在于激活函数tanh,tanh的倒数是1,所以在反向求梯度的时候,这个分支的值就不会越变越小,而是直接传递会去。所以当输入的激活函数改为了tanh之后,使得 C t C_t Ct?的计算就好比是一个残差结构,左侧虽然会使得梯度消失,但是右侧因为tanh激活后输入,反向梯度求解时,将永远是1,这就完美的将梯度回传,达到缓解梯度消失的问题。
至此LSTM的原理应该说完了。
LSTM实现(pytorch版本)
接口讲解
- **模型接口:torch.nn.LSTM(*args, kwargs)
参数(只列出常用的):
input_size :输入数据的大小,如果batch_first = False,则input_size数据形状为(sequence length,batch size, input size),否则为(batch size, sequence length,input size),如果以文本的生成预测为例,也就是用一句话的前几个字预测后面的字,那么sequence length就是整个句子的长度,input size就是一个词用数字表示(embedding)的大小。而batch size就不用说,就表示一次要送进去几句话进行训练
hidden_size :每一层隐藏层神经元个数
num_layers :有多少个隐藏层
batch_first :默认为False
dropout :如果为True,则表示每一次训练都会随机丢弃神经元。
bidirectional :如果为True,表示双向lstm,否则是单向,默认是单向。
-
输入数据格式
??以上是对LSTM网络的初始化设置,设置好之后,需要喂给模型的数据有两个,一个就是我们的输入数据,这个输入的数据和我们初始化lstm模型时设定的input_size大小是统一的,这个没什么疑问。
??另一个就是c_0和h_0,这两个我们在之前的原理中是讲过的,所以我们也需要初始化c和h,喂给lstm。
h_0大小为(Dnum_layers,batch size,hidden_size),这里如果是单向lstm,D = 1,如果是双向,则为2
注:这里对于h_0的最后一个维的设置并不止是hidden_size,它其实是受到,lstm里面的一个参数叫proj_size的控制,具体可看官网
c_0大小为(Dnum_layers,batch size,hidden_size) -
输出数据格式
模型会有三个输出,一个输出是预测结果输出output,大小为(sequence length,batch size, Dhidden size),或者(batch size, sequence length,Dhidden size)。
h_n:和h_0同大小
c_n:和c_0同大小
重要:
- 以上只是对模型接口、输入输出做了讲解,到具体的实际工作中,如果是做二分类预测,通常最后只有一个输出,所以还需要将lstm的输出拉平,然后接入一个全连接层,然后做sigmoid等工作。
- 有时候输入的数据并不对其,比如,如果是做文本预测生成的画,训练数据集中,可能有一句话很长,有的很短,但是给dataloader的数据又必须对齐:所以需要考虑对齐问题,可以看看官网的三个函数:
torch.nn.utils.rnn.pad_sequence() :实现数据补全,便于喂入dataloader
torch.nn.utils.rnn.pack_padded_sequence() :实现数据压缩,实时改变batch size。
torch.nn.utils.rnn.pad_packed_sequence():对数据进行补全,便于最后进入全连接层,导致数据不统一。