介绍:
卷积神经网络:是一类包含卷积计算且具有深度结构的前馈神经网络,是深度学习的代表算法之一,卷积神经网络具有表征学习能力,能够按其阶层结构对输入信息进行平移不变分类。卷积神经网络发展快速,并被应用于计算机视觉、自然语言处理等领域
卷积层
池化层
ReLU层
全连层
图片识别过程:
1、特征提取(卷积层)(自动提取)
2、提取主要特征(池化层)
3、特征汇总
4、产生分类器(全连层)进行预测识别
传统神经网络处理图片:通过全连的方式
图像是由一个个像素点构成,每个像素点有三个通道,分别代表RGB颜色,那么,如果一个图像的尺寸是(28,28,1),即代表这个图像的是一个长宽均为28,channel为1的图像(1为单通道已经是灰度的图片了)。
以全连的网络构造计算:网络中的神经与与相邻层上的每个神经元均连接,那就意味着我们的网络有28 * 28 =784个神经元,hidden层采用了15个神经元,那么简单计算一下,我们需要的参数个数(w和b)就有:7841510+15+10=117625个,这个参数太多了,随便进行一次反向传播计算量都是巨大的。
卷积神经网络——局部感受视野
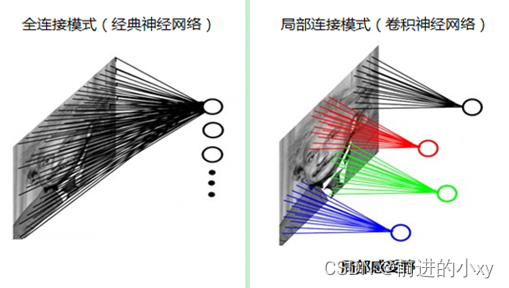
传统神经网络上每一个像素点都有一个神经元进行连接,导致特征点过多。
卷积神经网络进行区域的分块,找到每一区域最有代表的特征(局部感受视野)
卷积神经网络——权值共享
传统的神经网络:每个神经元只与前一层的局部神经元相连。层数越多需要计算的参数就越多。
权值共享:每个神经元的w值都是一样的。(参数就少了)
卷积神经网络解决了BP神经网路:全连层参数过多,运算量大,训练时间长和特征点过多的问题(局部感受全局)
卷积过程:
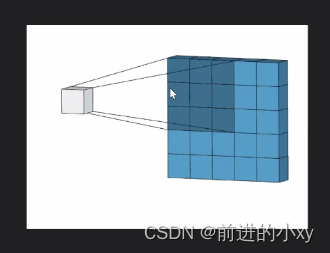
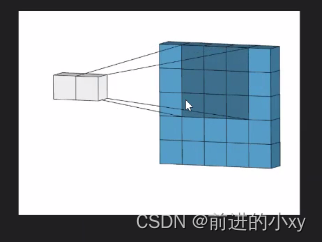
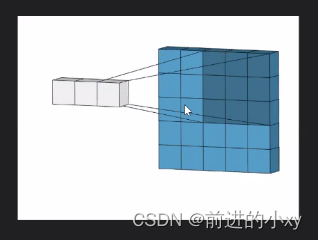
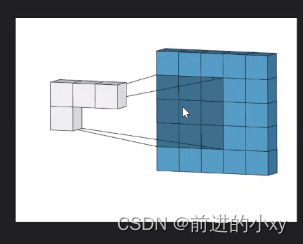
。
。
。
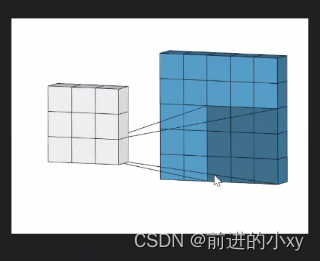
从55的格子变成33的格子这就是卷积的过程
权值共享:

在颜色深的区域中右下角的值就是权值,在右边的17是左边00+11+32+12+2*2.。。。所得。在卷积的过程中右下角的数值不会改变
特殊例子:
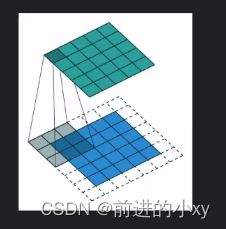
补边:在每个扫描区域中不够的格子补上白格子,格子的值为0
卷积过程
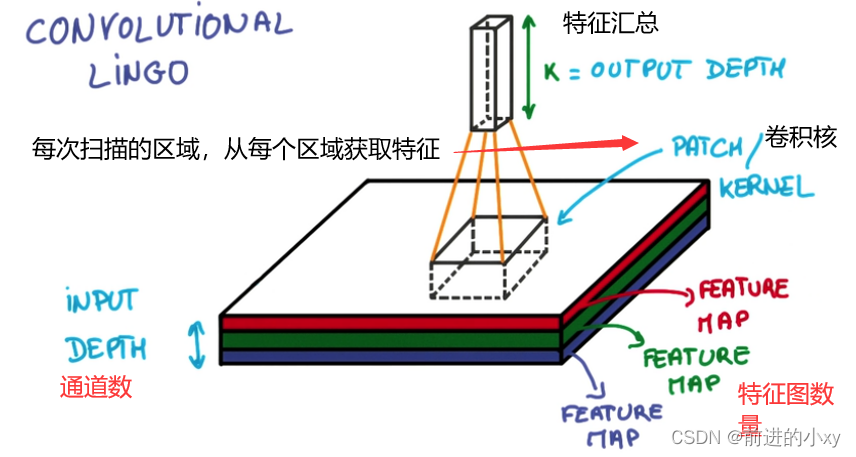
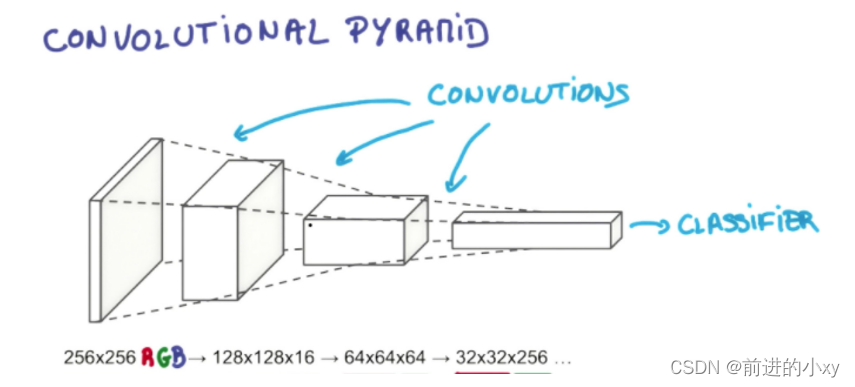
后面的卷积、池化、激活不只做一次在前一层的基础上继续做,从左往右的过程,特征数不断减少256->128->64… 深度变深3->16->64…最后通过全连层,创建分类器
卷积层
提取图片每个小部分里具有的特征
卷积输出
通过每一个feature(卷积核)的卷积操作,会得到一个新的二维数组,称之为feature map。其中的值,越接近1表示对应位置和feature的匹配越完整,越是接近-1,表示对应位置和feature的反面匹配越完整,而值接近0的表示对应位置没有任何匹配或者说没有什么关联。
池化层
池化就是将输入图像进行缩小,减少像素信息,只保留重要信息、也就是提取重要的特征信息。
通常情况下,池化区域是2*2大小,然后按一定规则转换成相应的值,例如取这个池化区域内的最大值(max-pooling)、平均值(mean-pooling)等,以这个值作为结果的像素值。
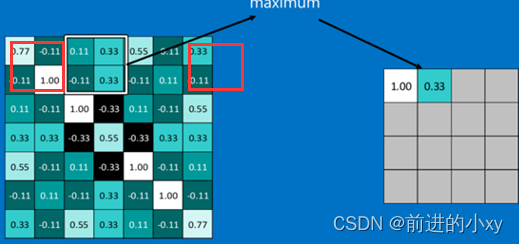
获取的是每个框中最大的数,像最右边的红框内右两个无内容的补0
激活层(ReLU)
激活函数的作用是用来加入非线性因素,把卷积层输出结果做非线性映射。
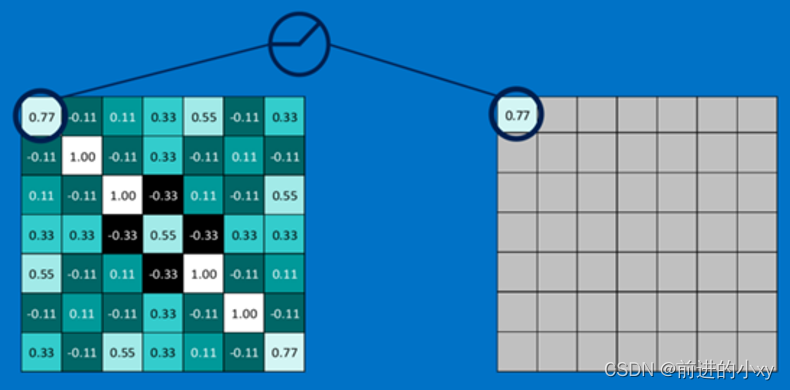
将值与0做对比,大于0留下,小于0取0。
卷积、激活、池化三层组合在一起使用
全连接层
起到分类器的作用,对结果进行识别分类
卷积神经网络过程
两阶段,四步
1、向前传播过程
1、从样本集中读取(X,Y),将X输入网络
2、计算相应的实际输出0P
2、向后传播阶段
1、计算实际输出和理想输出的差值
2、按极小误差发反向传播调整权值矩阵。
函数实现:
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
# 加载数据 进行独热编码
mnist_data = input_data.read_data_sets("MNIST_data/", one_hot=True)
# 输入像素点个数
input_size = 28 * 28
# 分类
num_class = 10
def weight_variable(shape):
"""
构建权重w 产生随机变量
"""
w = tf.random_normal(shape=shape, stddev=0.01)
return tf.Variable(w)
def bias_variable(shape):
"""
构建偏置b
:param shape:
:return:
"""
b = tf.constant(0.01, shape=shape)
return tf.Variable(b)
def con2d(x, w):
"""
卷积层准备:函数实现
:param x: 图像矩阵信息
:param w: 卷积核值
strides 卷积步长[上右下左]
padding:
SAME:补原来一样大小的
VALID:缩小,不够的地方不补充
:return: conv2d 卷积函数
"""
return tf.nn.conv2d(x, w, strides=[1, 1, 1, 1], padding='SAME')
def relu_con(x):
"""
激活卷积层 x与0比较
:param x:
:return:
"""
return tf.nn.relu(x)
def max_pool_con(x):
"""
池化层 小一倍数据
:param x:图片矩阵信息
ksize:
strides:步长
padding:与卷积的padding一样
:return:
"""
return tf.nn.max_pool(x,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')
# 网络搭建
# 特征标签的占位符
# xs输入特征值的像素 None表示行数 input_size表示列数
xs = tf.placeholder(tf.float32, shape=[None, input_size])
# ys识别的数字,有几种类别
ys = tf.placeholder(tf.float32, shape=[None, num_class])
# 28*28的矩阵 -1任意张 1表示深度
x_image = tf.reshape(xs, [-1, 28, 28, 1])
# CNN构建
# 第一层
# 卷积层 卷积核patch=5*5 输入数据的维度--1 输出高度--32
# 为什么是1?
# 因为输入的图片是灰度处理后的所以是1
w_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])
# 卷积
conv1 = con2d(x_image,w_conv1)
# 激活
h_conv1 = relu_con(conv1+b_conv1)
# 池化
h_pool1 = max_pool_con(h_conv1)
# 第二层
# 上面的输出下面的输入
w_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
# 卷积
conv2 = con2d(h_pool1,w_conv2)
# 激活
h_conv2 = relu_con(conv2+b_conv2)
# 池化
h_pool2 = max_pool_con(h_conv2)
# 全连层 实现数据拍平、分类
# 全连层1:前馈神经网络
# 第二次池化后的输出
# 原input_size=28一层池化后少一半前面有两层此处就是7,前面输出64所以是7*7*64
# 假设神经元个数1024(2的次方数)
w_fc1 = weight_variable([7*7*64,1024])
b_fc1 = bias_variable([1024])
# 输出矩阵 行不管 列:7*7*64
h_pool2_flat = tf.reshape(h_pool2,[-1,7*7*64])
# wx+b
h_fc1 = tf.matmul(h_pool2_flat,w_fc1)+b_fc1
# 激活
h_fc1 = relu_con(h_fc1)
# 全连层2:分类 输出
w_fc2 = weight_variable([1024,num_class])
b_fc2 = bias_variable([num_class])
# 计算激活
h_fc2 = tf.matmul(h_fc1,w_fc2)+b_fc2
# 激活——分类
predict = tf.nn.softmax(h_fc2)
# 构建损失函数 前面的文章有介绍
loss = tf.reduce_mean(-tf.reduce_mean(ys*tf.log(predict),reduction_indices=[1]))
# 优化器 梯度下降函数
Optimizer = tf.train.AdamOptimizer(0.0001).minimize(loss)
init = tf.global_variables_initializer()
# 训练次数
train_times = 500
# 分批训练
batch_size = 100
# 启动绘画,开始训练
with tf.Session() as sess:
sess.run(init)
for i in range(train_times):
batch_x,batch_y = mnist_data.train.next_batch(batch_size)
sess.run(Optimizer,feed_dict={xs:batch_x,ys:batch_y})
train_loss = sess.run(loss,feed_dict={xs:batch_x,ys:batch_y})
print(train_loss)
损失率逐渐下降的过程
总结:
各层作用:
卷积层:提取图片每个部分里具体特征。卷积核与数字矩阵对应位相乘相加,得到卷积层输出结果
池化:提取更重要的特征信息。通常2*2大小,参数padding是否需要补边。
激活:增加非线性因素,常用的激活函数有sigmoid、tanh、relu等等,前两者sigmoid/tanh比较常见于全连接层,后者ReLU常见于卷积层ReLU,它的特点是收敛快,求梯度简单。计算公式也很简单,max(0,T),即对于输入的负值,输出全为0,对于正值,则原样输出。
全连:第一层,做数据拍平。第二层输出分类器