findContours
contours,hierarchy = cv2.findContours(src,cv2.RETR_TREE,cv2.CHAIN_APPROX_SIMPLE)
参数
-
src 原图
-
cv2.RETR_TREE:提取轮廓后,输出轮廓信息的组织形式,除了cv2.RETR_TREE还有以下几种选项:
cv2.RETR_EXTERNAL:输出轮廓中只有外侧轮廓信息;
cv2.RETR_LIST:以列表形式输出轮廓信息,各轮廓之间无等级关系;
cv2.RETR_CCOMP:输出两层轮廓信息,即内外两个边界(下面将会说到contours的数据结构);
-
cv2.CHAIN_APPROX_SIMPLE:指定轮廓的近似办法,有以下选项:
cv2.CHAIN_APPROX_NONE:存储轮廓所有点的信息,相邻两个轮廓点在图象上也是相邻的;
cv2.CHAIN_APPROX_SIMPLE:压缩水平方向,垂直方向,对角线方向的元素,只保留该方向的终点坐标;
cv2.CHAIN_APPROX_TC89_L1:使用teh-Chinl chain 近似算法保存轮廓信息。
输出:contours,hierarchy
- contours:
list结构,列表中每个元素代表一个边沿信息。每个元素是(x,1,2)的三维向量,x表示该条边沿里共有多少个像素点,第三维表示每个点的横、纵坐标;
注意:如果输入选择cv2.CHAIN_APPROX_SIMPLE,则contours中一个list元素所包含的x点之间应该用直线连接起来,这个可以用cv2.drawContours()函数观察一下效果。 - hierarchy:返回类型是(x,4)的二维ndarray。x和contours里的x是一样的意思。如果输入选择cv2.RETR_TREE,则以树形结构组织输出,hierarchy的四列分别对应下一个轮廓编号、上一个轮廓编号、父轮廓编号、子轮廓编号,该值为负数表示没有对应项。
求长度:cv2.arcLength(contours[i],False)
可以看到第二个参数是选择False还是True。这个参数指定识别的contours是否闭合,True对应闭合,False对应非闭合。
求面积:cv2.contourArea(contours[i])
cv2.drawContours
cv2.drawContours(image, contours, contourIdx, color, thickness=None, lineType=None, hierarchy=None, maxLevel=None, offset=None)
参数:
- image: 指明在哪幅图像上绘制轮廓;image为三通道才能显示轮廓
- contours: 轮廓本身,在Python中是一个list;
- contourIdx:指定绘制轮廓list中的哪条轮廓,如果是-1,则绘制其中的所有轮廓。
- 后面的参数很简单。其中thickness表明轮廓线的宽度,如果是-1(cv2.FILLED),则为填充模式。
cv2.approxPolyDP
approx = cv2.approxPolyDP(cnt, epsilon,True)
输入
- cnt: [x,1,2]list列表
- epsilon Douglas-Peucker算法参数
- True 参数3表示是否闭合
输出:list列表,列表中每个元素代表一个边沿信息。每个元素是(x,1,2)的三维向量,x表示该条边沿里共有多少个像素点,第三维表示每个点的横、纵坐标;
cv2.approxPolyDP使用的是Douglas-Peucker算法,原理如下:
在数字化时,要对曲线进行采样,即在曲线上取有限个点,将其变为折线,并且能够在一定程度上保持原有的形状。经典的Douglas-Peucker算法步骤如下:
- 在曲线首尾两点A,B之间连接一条直线AB,该直线为曲线的弦;
- 得到曲线上离该直线段距离最大的点C,计算其与AB的距离d;
- 比较该距离与预先给定的阈值threshold的大小,如果小于threshold,则该直线段作为曲线的近似,该段曲线处理完毕;
- 如果距离大于阈值,则用C将曲线分为两段AC和BC,并分别对两段取信进行1~3的处理。
- 当所有曲线都处理完毕时,依次连接各个分割点形成的折线,即可以作为曲线的近似。
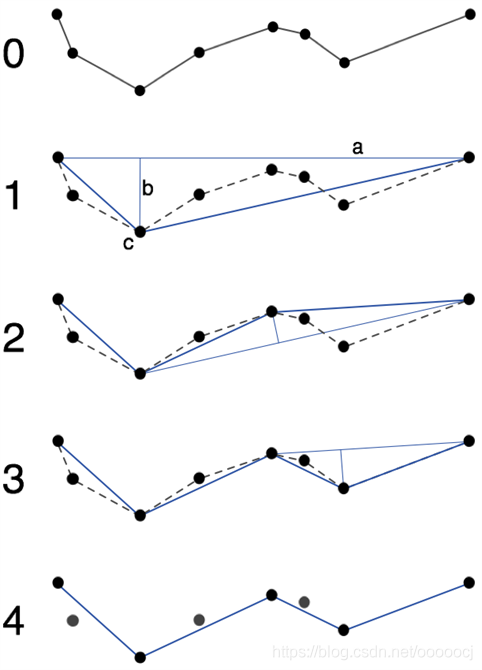
由此可见,设定的阈值越小,拟合的越精准,拟合后多边形的边和顶点越多。cv2.approxPolyDP的参数2(epsilon)是一个距离值,表示多边形的轮廓接近实际轮廓的程度,值越小,越精确。虽然不确定epsilon是不是就是threshold,但肯定和threshold是正相关的。参数3表示是否闭合。
cv2.boundingRect
矩形边框(Bounding Rectangle)是说,用一个最小的矩形,把找到的形状包起来。还有一个带旋转的矩形,面积会更小,效果见下图:

x,y,w,h = cv2.boundingRect(img)
cv2.rectangle(img, (x, y), (x+w, y+h), (0, 255, 0), 2)
# 用红色表示有旋转角度的矩形框架
rect = cv2.minAreaRect(cnt)# 得到最小外接矩形的(中心(x,y), (宽,高), 旋转角度)
box = cv2.cv.BoxPoints(rect)# 获取最小外接矩形的4个顶点坐标(ps: cv2.boxPoints(rect) for OpenCV 3.x)
box = np.int0(box)
cv2.drawContours(img, [box], 0, (0, 0, 255), 2)
cv2.imwrite('contours.png', img)
minEnclosingCircle
在Opencv中,求最小包围圆的函数:
center, radius=cv.minEnclosingCircle(points)
cv2.minEnclosingCircle(contours[0])
返回值:
- center:圆的中心
- radius:半径