[人工智能]python实现图像添加噪声、噪声处理、滤波器代码实现

目录

加载图像添加噪声

图像傅里叶变换和反变换并可视化

图像处理---高通滤波、低通滤波、带通滤波

低通滤波器---Butterworth低通滤波器、理想低通滤波器、高斯低通滤波器

加载图像添加噪声

• 高斯噪声是指它的概率密度函数服从高斯分布（即正态分布）的一类噪声
• 椒盐噪声也称为脉冲噪声，是图像中经常见到的一种噪声，它是一种随机出现的白点或者黑点，可能是亮的区域有黑色像素或是在暗的区域有白色像素（或是两者皆有）
• 乘性噪声一般由信道不理想引起，它们与信号的关系是相乘，信号在它在，信号不在他也就不在

import numpy as np
import cv2
import matplotlib.pyplot as plt
import skimage
from skimage import io
import random

#img = cv2.imread('E:/python/CSDN/image/1.bmp',cv2.IMREAD_GRAYSCALE)
img = plt.imread('E:/python/CSDN/image/5.bmp')

fig=plt.figure(figsize=(10, 50))
#显示原图
plt.subplot(12,3,1),plt.imshow(img,'gray'),plt.title('original')

def addGaussNoise(origin,var=0.0005):#添加高斯噪声函数
    #var = random.uniform(0.0001, 0.04)
    noisy = skimage.util.random_noise(origin, mode='gaussian', var=var)
    return noisy

def addSaltNoise(origin,var=0.01):#添加椒盐噪声函数
    #var = random.uniform(0.01, 0.2)
    noisy = skimage.util.random_noise(origin, mode='s&p', amount=var)
    return noisy

def addSpeckleNoise(origin,var=0.001):#添加乘法噪声函数
    #var = random.uniform(0.0001, 0.04)
    noisy = skimage.util.random_noise(origin, mode='speckle', var=var)
    return noisy

img = addGaussNoise(img)
#img = addSaltNoise(img)
#img = addSpeckleNoise(img)
#显示添加高斯噪声的原图
plt.subplot(12,3,4),plt.imshow(img,'gray'),plt.title('img_add_gaussin')

图像傅里叶变换和反变换并可视化

#进行傅立叶变换，并显示结果
fft2 = np.fft.fft2(img)
plt.subplot(12,3,2),plt.imshow(np.abs(fft2),'gray'),plt.title('fft2')

#将图像变换的原点移动到频域矩形的中心，并显示效果
shift2center = np.fft.fftshift(fft2)
plt.subplot(12,3,3),plt.imshow(np.abs(shift2center),'gray'),plt.title('shift2center')

#保存图片
#cv2.imwrite("E:/python/CSDN/image/fft.jpg",np.abs(fft2))
#cv2.imwrite("E:/python/CSDN/image/fftshift.jpg",np.abs(shift2center))

#由于傅里叶系数的动态范围过大，无法在屏幕上显示，为了便于观察，利用对数变换将这些较大的系数值变小。经过对数变换之后，较高的数值会变成白点，而较小的数值变为黑点。为了将灰度值可视化。

#对傅立叶变换的结果进行对数变换，并显示效果
log_fft2 = np.log(1 + np.abs(fft2))
plt.subplot(12,3,5),plt.imshow(log_fft2,'gray'),plt.title('log_fft2')

#对中心化后的结果进行对数变换，并显示结果
log_shift2center = np.log(1 + np.abs(shift2center))
plt.subplot(12,3,6),plt.imshow(log_shift2center,'gray'),plt.title('log_shift2center')

#原图反变换
f_image = np.fft.ifftshift(shift2center)
image_new = np.fft.ifft2(f_image)   # 反变换的结果是复数
image_new = np.abs(image_new)

图像处理---高通滤波、低通滤波、带通滤波

• ??? 高通滤波：高频信息通过，低频信息被阻挡；
• ? ? 低通滤波：低频信息通过，高频信息被阻挡；
• ? ? 带通滤波：介于低频和高频之间的一带信息通过，其它信息被阻挡；

#区域越小越接近原图
up_high = 10
left_high = 15
# 掩膜-中心为0-高通滤波
rows,cols = img.shape
print("high pass{},{}".format(rows,cols))
mask0 = np.ones(img.shape)
mask0[int(rows/2-up_high):int(rows/2+up_high), int(cols/2-left_high):int(cols/2+left_high)] = 0
fshift_mask0 = shift2center*mask0
#plt.subplot(12,3,8),plt.imshow(np.abs(fshift_mask0),'gray'),plt.title('fshift_mask0')
# 二维傅里叶反变换
f_image_mask0 = np.fft.ifftshift(fshift_mask0)
image_new0 = np.fft.ifft2(f_image_mask0)   # 反变换的结果是复数
image_new0 = np.abs(image_new0)
plt.subplot(12,3,8),plt.imshow(np.abs(image_new0),'gray'),plt.title('highPassFilter')

#保存图片
#cv2.imwrite("E:/python/CSDN/image/fshift_mask_high.jpg",np.abs(fshift_mask0))
#cv2.imwrite("E:/python/CSDN/image/image_new_high.jpg",np.abs(image_new0))

#区域越大越接近原图
up_low = 50
left_low = 15
# 掩膜-中心为1-低通滤波
rows,cols = img.shape
print("low pass {},{}".format(rows,cols))
mask1 = np.zeros(img.shape)
mask1[int(rows/2-up_low):int(rows/2+up_low), int(cols/2-left_low):int(cols/2+left_low)] = 1
fshift_mask1 = shift2center*mask1
#plt.subplot(12,3,10),plt.imshow(np.abs(fshift_mask1),'gray'),plt.title('fshift_mask1')
# 二维傅里叶反变换
f_image_mask1 = np.fft.ifftshift(fshift_mask1)
image_new1 = np.fft.ifft2(f_image_mask1)   # 反变换的结果是复数
image_new1 = np.abs(image_new1)
plt.subplot(12,3,9),plt.imshow(np.abs(image_new1),'gray'),plt.title('lowPassFilter')

# 带通滤波
w = 50 #带宽
radius = 20 #带中心到频率平面原点的距离
rows,cols = img.shape
print("low pass {},{}".format(rows,cols))
mask1 = np.ones(img.shape)
for i in range(0, rows):
    for j in range(0, cols):
        # 计算(i, j)到中心点的距离
        from math import sqrt
        d = sqrt(pow(i - rows, 2) + pow(j - cols, 2))
        if radius - w / 2 < d < radius + w / 2:
            mask1[i, j] = 0
        else:
            mask1[i, j] = 1

fshift_mask1 = shift2center*mask1
#plt.subplot(12,3,10),plt.imshow(np.abs(fshift_mask1),'gray'),plt.title('fshift_mask1')
# 二维傅里叶反变换
f_image_mask1 = np.fft.ifftshift(fshift_mask1)
image_new1 = np.fft.ifft2(f_image_mask1)   # 反变换的结果是复数
image_new1 = np.abs(image_new1)
plt.subplot(12,3,7),plt.imshow(np.abs(image_new1),'gray'),plt.title('bandPassFilter')

低通滤波器---Butterworth低通滤波器、理想低通滤波器、高斯低通滤波器

低通滤波器的功能是让低频率通过而滤掉或衰减高频，其作用是过滤掉包含在高频中的噪声。即低通滤波的效果是图像去噪声平滑增强，但同时也抑制了图像的边界即过滤掉图像细节，造成图像不同程序上的模糊。

• 理想低通滤波器的滤波非常尖锐
• 高斯低通滤波器的滤波则非常平滑
• 巴特沃斯滤波器介于两者之间，当巴特沃斯低通滤波器的阶数较高时，接近于理想低通滤波器；当巴特沃斯低通滤波器的阶数较高时，则接近于高斯低通滤波器。

# Butterworth低通滤波器的实现函数的定义
def ButterworthPassFilter(image, d, n): # 定义一个Butterworth低通滤波器
    f = np.fft.fft2(image)              # 快速傅里叶变换算法得到频率分布
    fshift = np.fft.fftshift(f)         # 将图像中的低频部分移动到图像的中心，默认是在左上角
    # fft结果是复数, 其绝对值结果是振幅；取对数的目的是将数据变换到0~255
    fimg = np.log(np.abs(fshift))

    def make_transform_matrix(d):     
        # 创建一个与输入图像同大小的全0矩阵，用于存储变化后的图像
        transform_matrix = np.zeros(image.shape)
        # 中心点值的计算，元组形式
        center_point = tuple(map(lambda x: (x - 1) / 2, fimg.shape))
        for i in range(transform_matrix.shape[0]):              # 行遍历
            for j in range(transform_matrix.shape[1]):          # 列遍历
                def cal_distance(pa, pb):                       # 欧拉距离计算函数的定义
                    from math import sqrt
                    dis = sqrt((pa[0] - pb[0]) ** 2 + (pa[1] - pb[1]) ** 2)
                    return dis
                dis = cal_distance(center_point, (i, j))        # 求出每个点与中心点的距离
                # 巴特沃斯低通滤波的数学公式实现
                transform_matrix[i, j] = 1 / (1 + (dis / d) ** (2 * n)) 
        return transform_matrix

    d_matrix = make_transform_matrix(d)                                  # 调用自定义函数
    new_img = np.abs(np.fft.ifft2(np.fft.ifftshift(fshift * d_matrix)))  # 生成新图
    return new_img

print("ButterworthPassFilter {}".format(img.shape))
butter_25_5 = ButterworthPassFilter(img,15, 5)  # Butterworth低通滤波处理
plt.subplot(12,3,10),plt.imshow(butter_25_5,'gray'),plt.title('ButterworthPassFilter')
#cv2.imwrite("E:/python/CSDN/image/ButterworthPassFilter.jpg",butter_25_5)


# 理想低通滤波器的实现函数的定义
def perfectPassFilter(image, d): # 定义一个理想低通滤波器
    f = np.fft.fft2(image)              # 快速傅里叶变换算法得到频率分布
    fshift = np.fft.fftshift(f)         # 将图像中的低频部分移动到图像的中心，默认是在左上角
    # fft结果是复数, 其绝对值结果是振幅；取对数的目的是将数据变换到0~255
    fimg = np.log(np.abs(fshift))

    def make_transform_matrix(d):     
        # 创建一个与输入图像同大小的全0矩阵，用于存储变化后的图像
        transform_matrix = np.zeros(image.shape)
        # 中心点值的计算，元组形式
        center_point = tuple(map(lambda x: (x - 1) / 2, fimg.shape))
        for i in range(transform_matrix.shape[0]):              # 行遍历
            for j in range(transform_matrix.shape[1]):          # 列遍历
                def cal_distance(pa, pb):                       # 欧拉距离计算函数的定义
                    from math import sqrt
                    dis = sqrt((pa[0] - pb[0]) ** 2 + (pa[1] - pb[1]) ** 2)
                    return dis
                dis = cal_distance(center_point, (i, j))        # 求出每个点与中心点的距离
                # 理想低通滤波
                if dis<=d:  #根据理想低通滤波器产生公式,当D(i,j)<=D0,置为1 
                    transform_matrix[i, j] = 1
                
        return transform_matrix

    d_matrix = make_transform_matrix(d)                                  # 调用自定义函数
    new_img = np.abs(np.fft.ifft2(np.fft.ifftshift(fshift * d_matrix)))  # 生成新图
    return new_img

print("perfectPassFilter {}".format(img.shape))
perfectPass = perfectPassFilter(img,20)  # 理想低通滤波处理
plt.subplot(12,3,11),plt.imshow(perfectPass,'gray'),plt.title('perfectPassFilter')
#cv2.imwrite("E:/python/CSDN/image/perfectPassFilter.jpg",perfectPass)

# 高斯低通滤波器的实现函数的定义
def gaussinlowPassFilter(image, d): # 定义一个高斯低通滤波器
    f = np.fft.fft2(image)              # 快速傅里叶变换算法得到频率分布
    fshift = np.fft.fftshift(f)         # 将图像中的低频部分移动到图像的中心，默认是在左上角
    # fft结果是复数, 其绝对值结果是振幅；取对数的目的是将数据变换到0~255
    fimg = np.log(np.abs(fshift))

    def make_transform_matrix(d):     
        # 创建一个与输入图像同大小的全0矩阵，用于存储变化后的图像
        transform_matrix = np.zeros(image.shape)
        # 中心点值的计算，元组形式
        center_point = tuple(map(lambda x: (x - 1) / 2, fimg.shape))
        for i in range(transform_matrix.shape[0]):              # 行遍历
            for j in range(transform_matrix.shape[1]):          # 列遍历
                def cal_distance(pa, pb):                       # 欧拉距离计算函数的定义
                    from math import sqrt
                    dis = sqrt((pa[0] - pb[0]) ** 2 + (pa[1] - pb[1]) ** 2)
                    return dis
                dis = cal_distance(center_point, (i, j))        # 求出每个点与中心点的距离
                # 高斯低通滤波
                from math import exp
                transform_matrix[i, j] = exp(-(dis*dis)/(2*(d**2))); #根据高斯低通滤波器公式H(u,v)=e^-[D^2(u,v)/2*D0^2]
                
        return transform_matrix

    d_matrix = make_transform_matrix(d)                                  # 调用自定义函数
    new_img = np.abs(np.fft.ifft2(np.fft.ifftshift(fshift * d_matrix)))  # 生成新图
    return new_img

print("gaussinlowPassFilter {}".format(img.shape))
gaussinlowPassFilter = gaussinlowPassFilter(img,20)  # 高斯低通滤波处理
plt.subplot(12,3,12),plt.imshow(gaussinlowPassFilter,'gray'),plt.title('gaussinlowPassFilter')

?各阶段图像示例：

?
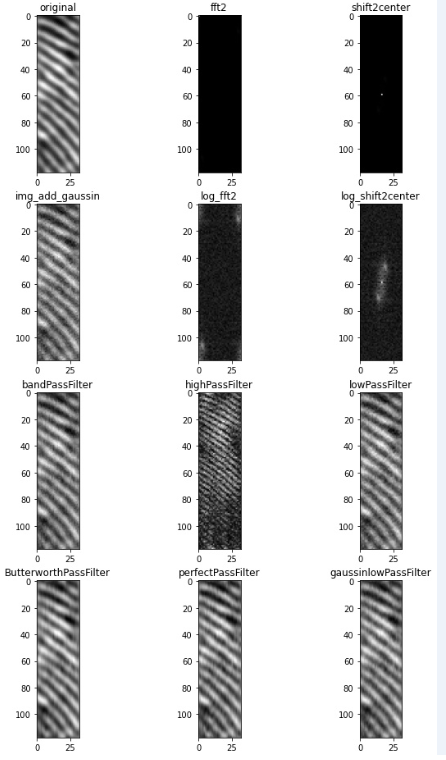