Chat
文章是莫纳什 潘世瑞组的,(已经于今年暑期从莫纳什前往昆士兰),ARGA作者,这个组关于图对比学习的文章挺多,但是开源文章较少
本文rank:
读起来很吸引人,motivation也很自然,个人认为是自从2019DGI出来之后,在DGI上认真考虑并修改的工作,揭示了DGI成功的原因。而并非采用不同增强的方法,或者借鉴cv方向对比学习的方法进行修改。
亮点: O1复杂度,1epoch就可以训练,取消判别器D训练损失提高可扩展,给出理论证明s(图级表征)的上下界
文章不足: OGB-arxiv可以full-batch,products,papers100M 仍然采用了graphsage进行采样,只是一定程度上增强了可扩展性,相较于aaai22 那篇sugrl在这方面还是不足
知识盲区
关于复杂度的知识,本文有提及: InfoNce损失 O(ND) JSD 损失是 O(D) BGRL(BYOL在graph上的扩展)和GBT(barlow twins在graph上的扩展) 取消了 负样本,但是相似性计算 仍然会让复杂度变成 O(D)
本文方法 GGD (graph group discrimination)
1. 出发点
本文从 不恰当的激活函数 sigmoid出发,探究DGI。 DGI通过最大化节点和图级表征s之间的互信息,从而成为对比学习在graph上的paradigm。

DGI存在的问题:DGI并不能像作者想象的那样来最大化互信息,DGI获得s的方法是 求平均,并会采用sigmoid激活。但是DGI的GNN(GCN)权重初始化采用 Xavier初始化,这样会使得 s 这个图级向量 都会接近于相同的数值 εI,ε是一个常数,I是一个全1向量
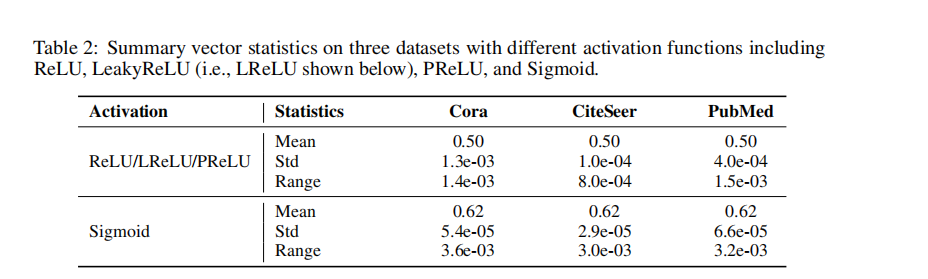
这个现象是实验得出的,作者提出定理1来进一步论证:

通过修改ε,作者从0变为1,做了以下实验,这些实验,表明这个s其实并没有多大作用 trivial。那么DGI的假设:通过对比h和s似乎并不是真正成功的原因
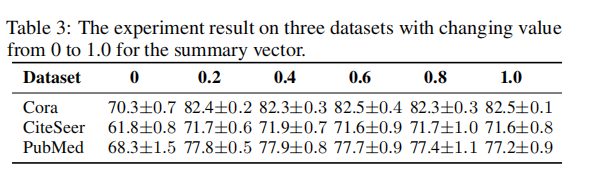
重点修改:
从上面来看 这个s很小作用,并且最终常常趋近于epsilonI,因此作者采用I(全1,epsilon=1)来直接代替这个s。这样做的好处: 不需要鉴别器了!!! 鉴别器D是一个基于bilinear的打分,需要对于每个节点和s进行打分,这个在样本对之间的乘法 通常会在前向和反向传播 消耗很多,

因此 DGI的损失成为:

其中,sum(zi)是因为zi (1D) 和s相乘,而s=1(D1),因此,表达的含义就是 zi的元素之和。 作者对于这个聚合也进行了变分,采用mean max linear来学习这个zi和s的结合方式 linear就说输出1D变成 11

sum和linear比较好
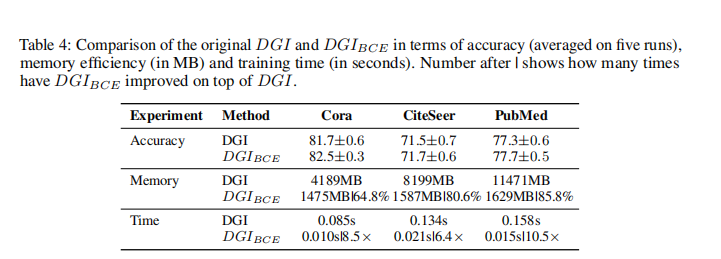
和DGI的对比,显著减小内存,Pubmed居然才需要 1629MB!!! 时间上也更快
基于上面的sum公式1,本文提出简化版的 BCE的DGI
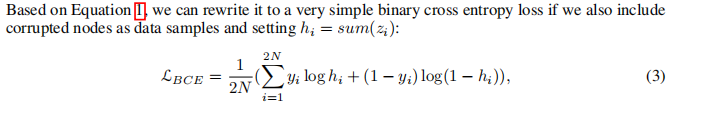
是一种二元交叉熵的形式,当节点属于原来的图,yi=1,节点属于被 破坏的图,yi=0, 这样的形式 就是 将两个图的所有节点进行 对比,判断h是原图还是被破坏的图,节点节点之间的对比:称为 group discrimination
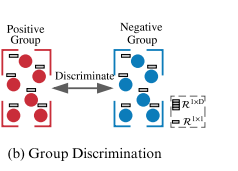
MVGRL的实验,进一步说明 group discrimination
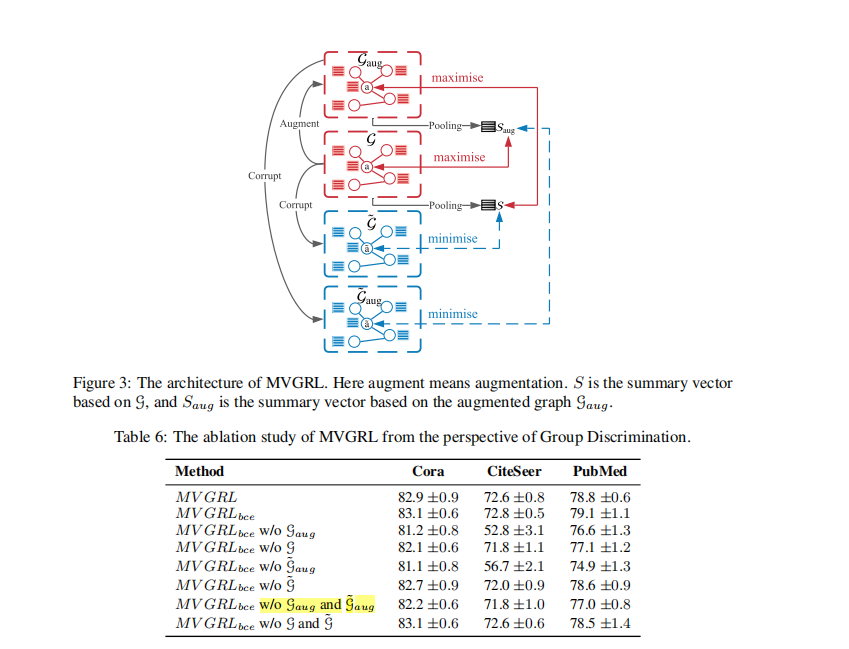
MVGRL通过diffusion 来augmented graph,从而多个视图之间进行对比,作者修改了他们的损失,形成bce MVGRL,也是ok的, ,,, 因为 这是 DGI的变分,也是采用了h和s之前最大化互信息
本文的model
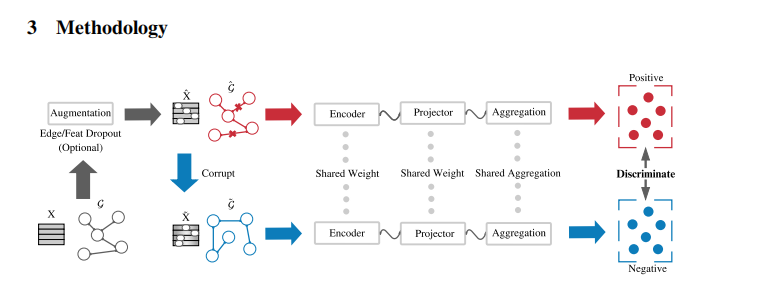
1. 通过边和节点drop来增强
注意 这里不是来获得多个增强的视图进行对比,而是 每一轮 不同的增强视图 会增加鲁棒性
2. Corrupt
和 DGI一样,成行shuffle X
3.Siamese GNN = GNN encoder+projector
本文采用GCN作为encoder, projector是自定义的多层linear layers。 共享的GNN来输出 原图和 corrupt之后图的节点表征。 在进行第四步之前,所有样本先要采用相同的 聚合方式(sum mean max linear) hi=sum(zi)
4.group discrimination
BCE损失,yi=1,原图。 yi负样本。 采用hi和yi进行bce损失
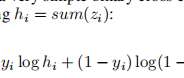
tricks

GNNencoder 输出的H,通过几次 和邻接矩阵相乘 获得增强的H,和原来的H进行之和,从而进行下游任务
discussion
NCE和JSD损失
nce的分子 对于节点i需要zi和ci相乘1次,分母需要zi和整体相乘 整体一共N次,两个向量zi 1d和 ci 1d相乘 需要耗费 O(D)次。因此 InfoNCE整体是 O(ND) 。
JSD对于每个节点不需要 N个负样本进行对比,但是 判别器还是需要 zi和ci相乘 O(D)。

BRGL和GBT
BRGL 通过 最大化zi和hi余弦相似性(负号),只用关注自身(自己和自己对应的拉)
GBT 基于相关性,GBT的损失就类似于一个 协方差矩阵 ii越大越好,ij越小越好。
但这两个损失还是包括 了 两个向量相乘。和JSD一样是O(D)。
本文是 h和一个常量相乘,就相当于是 把 乘法变成 做加法。

由于是乘法问题,这里是通过加法,是否两个向量 做减法,能够相似性呢?--------- 引出了 基于margin loss的对比损失 aaai22 和接下来 要写的一篇文章subCon–icdm
实验
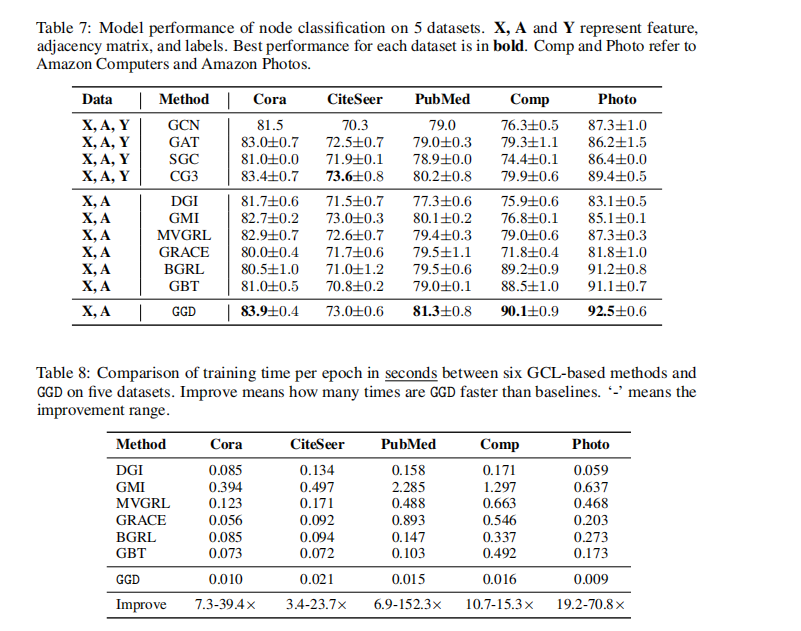
full-batch下,特别 节约内存
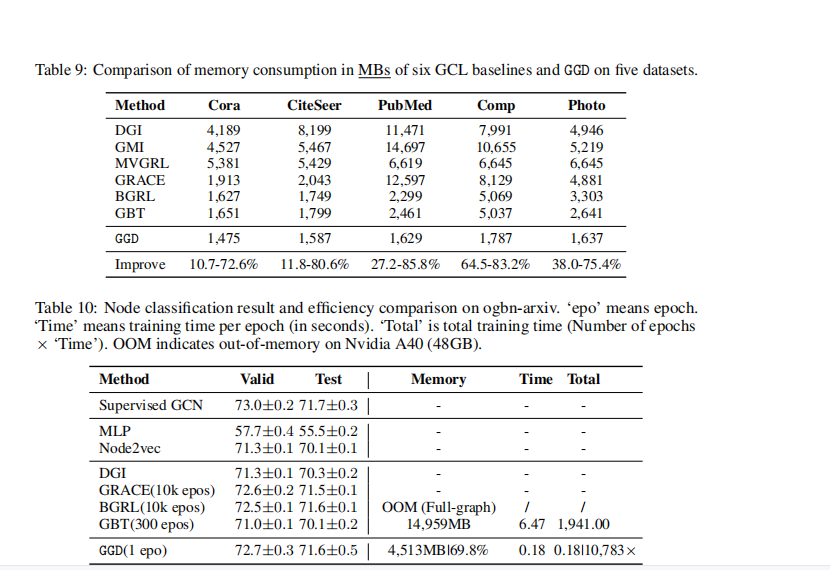
基于采样:graphsage
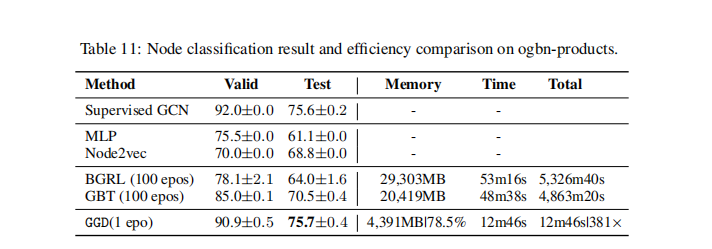
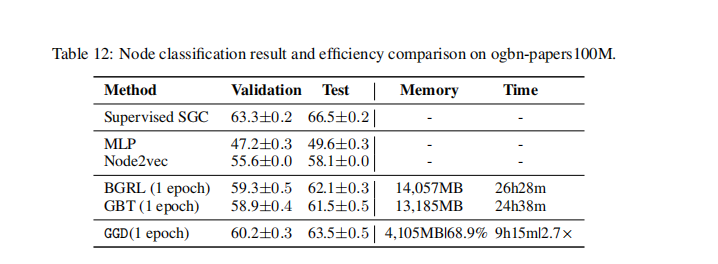
采样的超参数设置

丢掉D,如何来进行节点对之间的相似性判断,往前追溯,对比学习就是有度量学习的影子,如何判断表征之间的相似性问题 (内积–余弦,采用bilinear–dgi,采用margin—做减法,采用拼接–contact linear输出)
Proof of Theorem1



