MetAug: Contrastive Learning via Meta Feature Augmentation

1. 摘要
??什么对对比学习很重要?我们认为对比学习在很大程度上依赖于信息特征,或“硬”(正面或负面)特征。早期的作品通过应用复杂的数据增强和大批量或内存库来包含更多信息特征,最近的作品设计了精细的采样方法来探索信息特征。探索这些特征的关键挑战是源多视图数据是通过应用随机数据增强生成的,这使得始终在增强数据中添加有用信息是不可行的。因此,从这种增强数据中学习到的特征的信息量是有限的。作为回应,我们建议直接增强潜在空间中的特征,从而在没有大量输入数据的情况下学习判别表示。我们执行元学习技术来构建增强生成器,通过考虑编码器的性能来更新其网络参数。然而,输入数据不足可能会导致编码器学习折叠的特征,从而导致增强生成器出现故障。在目标函数中进一步添加了一个新的边缘注入正则化,以避免编码器学习退化映射。为了在一个梯度反向传播步骤中对比所有特征,我们采用了提出的优化驱动的统一对比损失,而不是传统的对比损失。根据经验,我们的方法在几个基准数据集上实现了最先进的结果。
2. 动机以及贡献
存在的问题
- 传统的学习范式需要大量对进行对比,并且许多对对模型没有信息,即正对非常接近而负对已经在隐蔽的空间中相距甚远。
- 许多研究工作都致力于数据的强大增强,但是从增强数据中学习到的特征的信息量很难准确测量。
贡献
- 提出边际注入元特征增强,它直接增强潜在特征以生成信息丰富的和抗塌陷的特征。受益于这些特征,编码器可以有效地捕获判别信息。
- 提出优化驱动的统一对比,以在反向传播的一个步骤中包含所有可用特征,并通过测量配对特征对优化的贡献来加权配对特征的相似性。
3. 方法
??目标是通过执行自我监督对比学习来学习捕获在多个不同视图之间共享的信息的表示。形式上,我们假设输入多视图数据集为 X = { X 1 , X 2 , . . . , X N } X=\{X_1,X_2,...,X_N\} X={X1?,X2?,...,XN?},其中 N N N表示样本数。 X i X_i Xi?表示样本的 M M M个视图的集合,其中 i ∈ { 1 , . . . , N } i\in \{1,...,N\} i∈{1,...,N}。对于每一个样本 X i X_i Xi?,我们将 x i x_i xi?表示为一个随机变量,表示 x i ~ P ( X i ) x_i ~ P(X_i) xi?~P(Xi?), x i j x^j_i xij?表示第 i i i个样本的第 j j j个视图,其中 j ∈ { 1 , . . . , M } j\in\{1,...,M\} j∈{1,...,M}。
3.1 对比学习准备
- 基本的对比学习,略。
3.2 边缘注入元特征增强
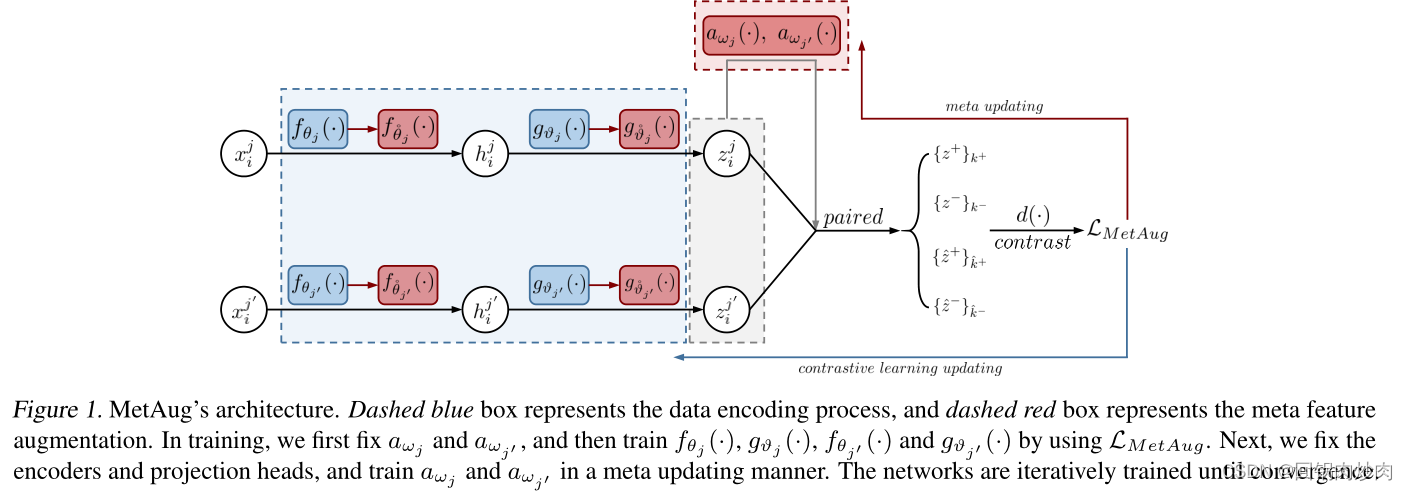
??基本思想是根据编码器的性能(梯度)来更新自身的网络参数来创建信息丰富的增强特征。整个 MetAug 架构的可视化如图 1 所示。
??首先为
M
M
M个视图构建一组MAGs(辅助元特征增强生成器)
a
ω
(
?
)
=
{
a
ω
1
(
?
)
,
.
.
.
,
a
ω
M
(
?
)
}
a_ω(·) = \{a_{ω_1}(·), ..., a_{ω_M} (·)\}
aω?(?)={aω1??(?),...,aωM??(?)},其中
ω
=
{
ω
1
,
.
.
.
,
ω
M
}
ω = \{ω_1, ..., ω_M\}
ω={ω1?,...,ωM?}。
f
θ
f_θ
fθ? 和
g
?
g_?
g??分别定义为视图特定编码器和投影头组,即
θ
=
{
θ
1
,
.
.
.
,
θ
M
}
θ = \{θ_1, ..., θ_M\}
θ={θ1?,...,θM?} 和
?
=
{
?
1
,
.
.
.
,
?
M
}
? = \{?_1, ..., ?_M\}
?={?1?,...,?M?}。
??在训练中,编码器
f
θ
(
?
)
f_θ(·)
fθ?(?) 和投影头
g
?
(
?
)
g_?(·)
g??(?) 与 MAG
a
ω
(
?
)
a_ω(·)
aω?(?) 一起训练(使用网络参数
ω
ω
ω)。遵循元学习协议,我们首先在自监督对比学习的学习范式下训练
f
θ
(
?
)
f_θ(·)
fθ?(?) 和
g
θ
(
?
)
g_θ(·)
gθ?(?)。然后,通过计算关于
f
θ
(
?
)
f_θ(·)
fθ?(?) 和
g
?
(
?
)
g_?(·)
g??(?) 性能的梯度来更新
a
ω
(
?
)
a_ω(·)
aω?(?)。在这里,当相应的对比损失被反向传播时,我们通过它们的梯度来衡量
f
θ
(
?
)
f_θ(·)
fθ?(?) 和
g
?
(
?
)
g_?(·)
g??(?) 的性能。具体来说,所有
f
θ
(
?
)
、
g
?
(
?
)
和
a
ω
(
?
)
f_θ(·)、g_?(·) 和 a_ω(·)
fθ?(?)、g??(?)和aω?(?) 都经过迭代训练,直到收敛。
伪代码

??具体来说,我们首先通过采用传统的对比损失来更新编码器和投影头的网络参数
θ
θ
θ 和
?
?
?。然后,我们以元学习的方式训练 MAG
a
ω
(
?
)
a_ω(·)
aω?(?)。我们鼓励增强特征提供信息,编码器
f
θ
(
?
)
f_θ(·)
fθ?(?) 可以通过联合使用原始特征和增强特征进行对比来更好地探索判别信息。因此,编码器的性能将在相同的训练数据上得到提升。为了更新
a
ω
(
?
)
a_ω(·)
aω?(?) 的网络参数
ω
ω
ω,我们将元更新目标形式化如下:
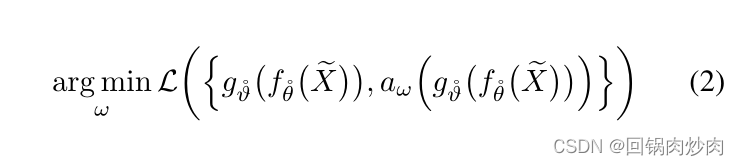
其中
X
~
\widetilde{X}
X
表示从训练数据集
X
X
X 中采样的小批量,
{
g
?
˙
(
f
θ
˙
(
X
~
)
)
,
a
ω
(
g
?
˙
(
f
θ
˙
(
X
~
)
)
)
}
\{g_{\dot{?}}(f_{\dot{θ}}(\widetilde{X})), a_ω(g_{\dot{?}}(f_{\dot{θ}}(\widetilde{X})))\}
{g?˙?(fθ˙?(X
)),aω?(g?˙?(fθ˙?(X
)))}表示包含原始特征和元增强特征的集合。
?
˙
\dot{?}
?˙和
θ
˙
\dot{θ}
θ˙分别表示编码器和投影头的参数集,它们是通过更新一个梯度反向传播来计算的:
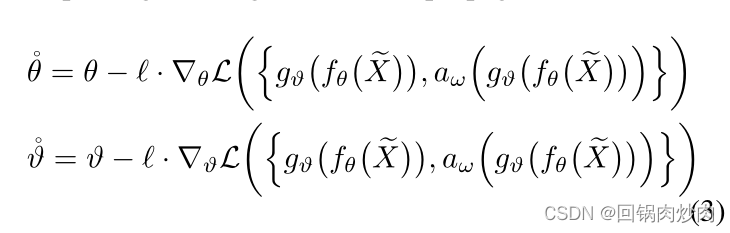
其中
?
?
? 是
θ
θ
θ 和
?
?
? 之间共享的学习率。元更新目标背后的想法是我们执行二阶导数技术来训练
a
ω
(
?
)
a_ω(·)
aω?(?)。具体来说,使用组合
{
θ
,
?
}
\{θ, ?\}
{θ,?} 的导数(Hessian 矩阵)的导数来更新
ω
ω
ω,其中
{
θ
,
?
}
\{θ, ?\}
{θ,?} 是连接
θ
θ
θ 和
?
?
? 的参数集。我们通过使用保留的
{
θ
,
?
}
\{θ, ?\}
{θ,?} 计算图来计算关于
ω
ω
ω 的导数。
??然而,在实践中,我们发现了一个关键问题:当原始特征信息量不足时,通过对比信息量不足的特征难以生成大梯度,MAGs
a
ω
(
?
)
a_ω(·)
aω?(?) 倾向于创建折叠的增强特征,例如,增强的特征和原始特征非常相似。我们认为特征崩溃的原因是编码器在投影头
g
?
(
f
θ
(
?
)
)
g_?(f_θ(·))
g??(fθ?(?)) 旁边的小梯度变化导致
a
ω
(
?
)
a_ω(·)
aω?(?) 的更新步长变得非常小,这使得
a
ω
(
?
)
a_ω( ·)
aω?(?) 陷入局部最优。增强的特征是这样的,没有任何额外的有用信息。为了解决这个问题,我们进一步注入了一个余量来鼓励
a
ω
(
?
)
a_ω(·)
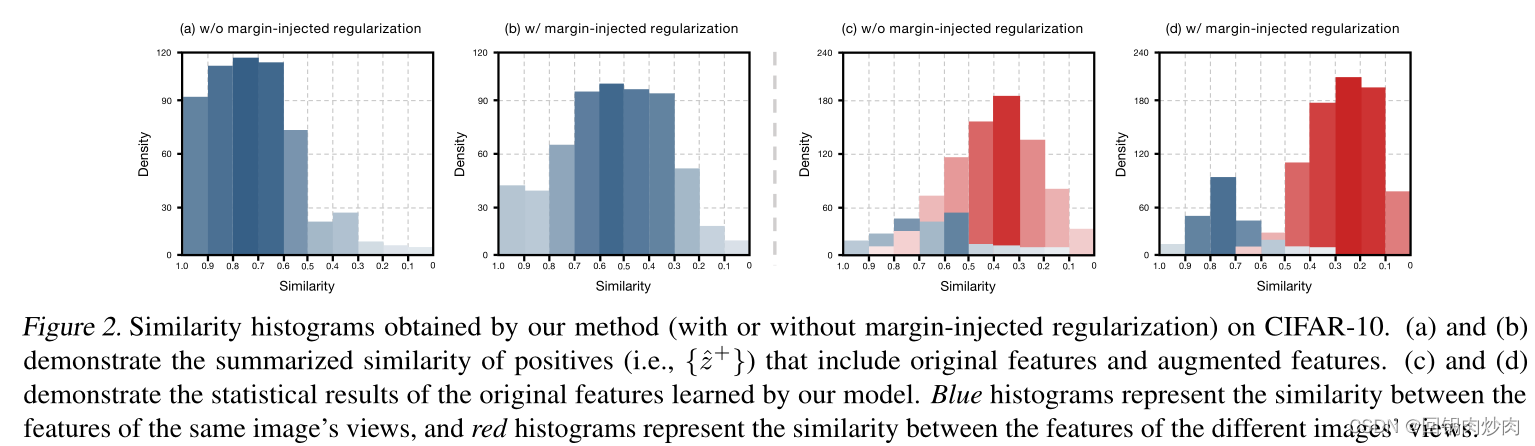
aω?(?) 生成更复杂和信息丰富的增强特征,这可以被认为是元更新目标中的正则化项。有关增强特征折叠问题的详细信息,请参见图 2(a),我们观察到,如果没有注入边距的正则化,MAG 往往会生成与原始特征非常相似的折叠特征。形式上,我们制定了为
a
ω
(
?
)
a_ω(·)
aω?(?) 生成边际的方法:
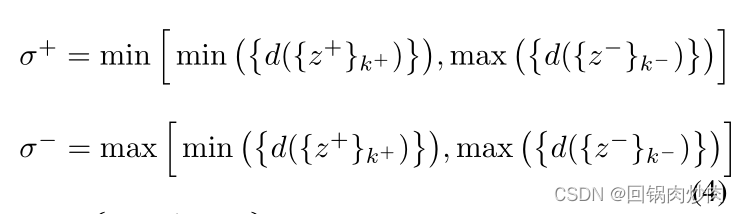
其中
{
d
(
{
z
+
}
k
+
)
}
\{d(\{z^+\}k^+)\}
{d({z+}k+)}是由判别函数
d
(
?
)
d(·)
d(?)和
k
+
∈
{
1
,
.
.
.
,
K
+
}
k^+∈ \{1, ..., K^+\}
k+∈{1,...,K+}计算的一组正例的输出(相似性),其中
K
+
K^+
K+表示小批量中正例的数量。
d
(
{
z
?
}
k
?
)
d(\{z^?\}k^?)
d({z?}k?)是负样本的判别输出的集合,并且
k
?
∈
{
1
,
.
.
.
,
K
?
}
k^?∈\{1, ..., K^?\}
k?∈{1,...,K?} 其中
K
?
K^?
K?表示负样本的数量。请注意,等式 4 中仅使用原始特征。我们将公式化的边际生成方法称为“大”,我们还提出了另外两种方法,称为“中”和“小”。在附录 A.2 中,我们进行了比较以评估三种利润生成方法的效果。我们通过在元更新目标中添加正则化项来注入增强特征和原始特征之间的边距,正则化定义为:
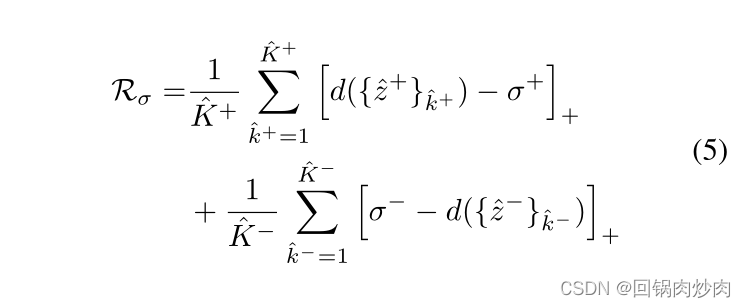
其中
{
z
^
+
}
k
^
+
\{\hat{z}^+\}_{\hat{k}^+}
{z^+}k^+?表示包含一个原始特征和一个增强特征的正例,
K
^
+
\hat{K}^+
K^+ 表示此类正例的数量。
{
z
^
?
}
k
^
?
\{\hat{z}^-\}_{\hat{k}^-}
{z^?}k^??表示同样的
K
^
?
\hat{K}^-
K^? 负数之一,每个负数包括一个原始特征和一个增强特征。
[
?
]
+
[·]_+
[?]+? 表示截止零函数,定义为
[
a
]
+
=
m
a
x
(
a
,
0
)
[a]_+ = max(a, 0)
[a]+?=max(a,0)。然后我们将这种正则化集成到
ω
ω
ω 的更新中
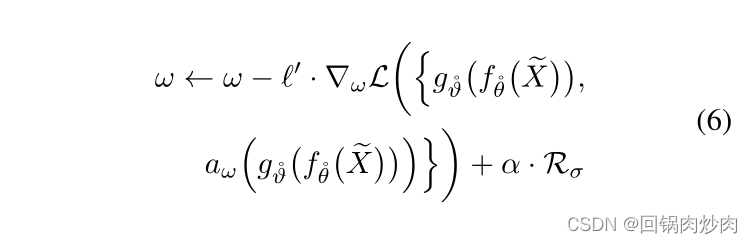
其中
?
′
?^′
?′ 表示
ω
ω
ω 的学习率,
α
α
α 是一个超参数,用于平衡边际注入正则化项损失的影响。
R
σ
R_σ
Rσ? 限制 MAGs 生成与原始特征更加不同的信息特征(参见图 2(b))。在实践中,图 2(c)和(d)表明我们的方法(带有边缘注入正则化)学习到的特征更加集中,例如,同一图像的特征更加相似,并且特征之间的差距不同的图像被放大,这证明了信息丰富的增强特征可以进一步引导编码器学习非折叠(分散)特征。
3.3 优化驱动的统一对比
??我们建议在一个梯度反向传播步骤中联合对比所有特征(包括原始特征和元增强特征)。我们引入了以下优化驱动的统一损失函数来代替传统的对比损失,如下所示:
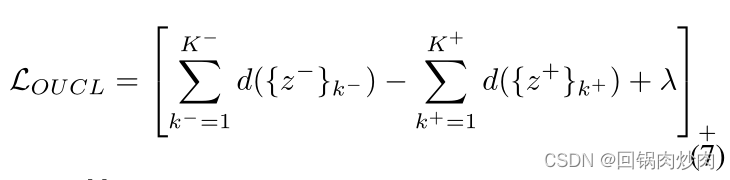
λ
λ
λ是汇总的实例相似度之间的边距,以增强相似度分离的能力。然而,我们发现
∑
k
?
=
1
K
?
d
(
{
z
?
}
k
?
)
\sum^{K^?}_{k^?=1}d(\{z^?\}_{k^?})
∑k?=1K??d({z?}k??)和
∑
k
+
=
1
K
+
d
(
{
z
+
}
k
+
)
\sum^{K^+}_{k^+=1}d(\{z^+\}_{k^+})
∑k+=1K+?d({z+}k+?)之间的差异并不是越大越好。差异的过度增加可能会破坏优化的收敛性。因此,我们希望采用导致更好收敛的余量
λ
λ
λ。我们通过添加一个温度系数
β
β
β来修改公式 7 中的损失,如下所示:
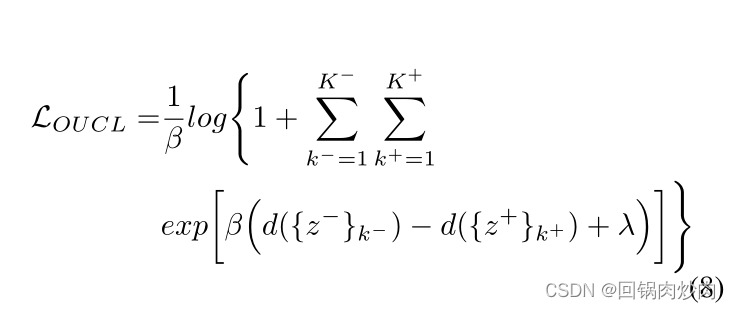
当
β
→
+
∞
β → +∞
β→+∞时,公式 8 等于公式 7。受 (Sun et al., 2020) 的启发,我们使用加权因子
Γ
?
Γ^?
Γ?和
Γ
+
Γ^+
Γ+来调节
d
(
{
z
?
}
k
?
)
d(\{z^?\}_{k^?})
d({z?}k??)和
d
(
{
z
+
}
k
+
)
d(\{z^+\}_{k^+})
d({z+}k+?)。这种方法旨在对偏离最优值的相似性给予更大的权重,对与最优值非常接近的相似性给予较小的权重。
Γ
?
=
[
d
(
{
z
?
}
k
?
)
?
O
?
]
+
Γ^? = [d(\{z^?\}_{k^?})?O^?]_+
Γ?=[d({z?}k??)?O?]+?和
Γ
+
=
[
O
+
?
d
(
{
z
+
}
k
+
)
]
+
Γ^+ = [O^+-d(\{z^+\}_{k^+})]_+
Γ+=[O+?d({z+}k+?)]+?,其中
O
?
O^?
O?和
O
+
O^+
O+表示
d
(
{
z
?
}
k
?
)
d(\{z^?\}_{k^?})
d({z?}k??)和
d
(
{
z
+
}
k
+
)
d(\{z^+\}_{k^+})
d({z+}k+?)的预期最优值。请注意,我们进一步提出了
Γ
Γ
Γ的变体,包括
Γ
?
Γ^-
Γ?和
Γ
+
Γ^+
Γ+,它们的比较在第 4.4 节中演示。
γ
+
γ^+
γ+和
γ
?
γ^?
γ?用于替换
λ
λ
λ并在公式8中添加
Γ
?
Γ^?
Γ?和
Γ
+
Γ^+
Γ+:
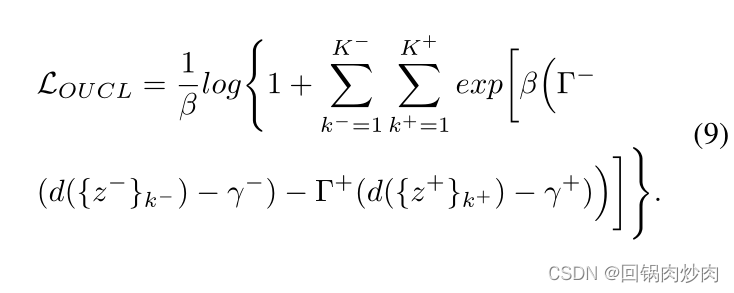
我们通过归一化
{
z
?
}
k
?
\{z^?\}_{k^?}
{z?}k??和
{
z
+
}
k
+
\{z^+\}_{k^+}
{z+}k+?中的特征,将
d
(
{
z
?
}
k
?
)
d(\{z^?\}_{k^?})
d({z?}k??)和
d
(
{
z
+
}
k
+
)
d(\{z^+\}_{k^+})
d({z+}k+?)限制在
[
0
,
1
]
[0, 1]
[0,1]的范围内,这样理论上,
d
(
{
z
?
}
k
?
)
d(\{z^?\}_{k^?})
d({z?}k??)的最优值为 0,
d
(
{
z
+
}
k
+
)
d(\{z^+\}_{k^+})
d({z+}k+?)的最优值为 1。
d
(
{
z
?
}
k
?
)
?
O
?
d(\{z^?\}_{k^?})?O^?
d({z?}k??)?O?和
O
+
?
d
(
{
z
+
}
k
+
)
O^+-d(\{z^+\}_{k^+})
O+?d({z+}k+?)可以很容易地得到保证。为了减少超参数的数量,我们将等式 9 改造成:
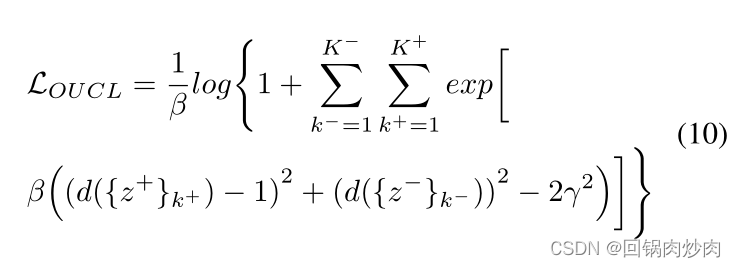
其中,
O
+
=
1
+
γ
、
O
?
=
?
γ
、
γ
+
=
1
?
γ
、
γ
?
=
γ
O^+ = 1 + γ、O^- = -γ、γ^+ = 1 - γ 、 γ^- = γ
O+=1+γ、O?=?γ、γ+=1?γ、γ?=γ
3.4 模型目标
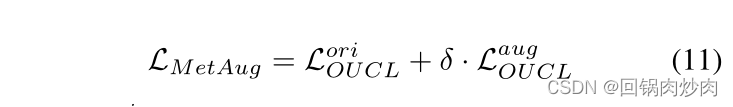
其中
L
O
U
C
L
o
r
i
L^{ori}_{OUCL}
LOUCLori?表示不包括元增强特征的损失,
L
O
U
C
L
a
u
g
L^{aug}_{OUCL}
LOUCLaug?表示包括这些特征的损失,
δ
δ
δ是控制它们之间平衡的系数。