[人工智能]发票表格检测——传统图像方法

前言

偶尔整理笔记，发现两三年前写的纯用opencv实现发票图片中的表格检测的笔记。虽然现在已经是深度学习网络的天下，但是回头看看过去的探索，感觉还是有点意思的，主要用来给我自己做个笔记备份，同时分享给踏入图像的初学者们呀~

0 简介

ocr的识别基本实现了通用识别功能之后，还需要实现发票、户口本等的识别，但是想要实现发票等有表格的文件的识别，还需要额外的处理。因为传统的文字框检测工具yolo会将一行文字一起识别。而发票这类表格数据，即使在同一行中，也因为竖线的划分，所以并不能认为是一行是一体的。

对于这种问题，我的思路就是首先将图片按照表格拆分成子图，然后将每个子图放入后续的文字识别框架单独识别，最后将所有的结果整合之后返回给用户。加上前前后后的处理过程，大致可以分为如下几步：

1. 判断图片是否需要大角度旋转（90,180,270）
2. 判断是否需要小角度的旋转，保证横线的水平
3. 使用opencv对表格的小矩形框进行提取
4. 对表格以外的区域进行划分（如上图所示）
5. 将所有的子图送入ocr模型进行检测
6. 拼接结果

这里主要介绍一下在进行2,3,4图像处理过程中使用的函数工具以及部分拓展阅读。先列出对我帮助非常大的文章

1. 要点初见：Python+OpenCV校正并提取表格中的各个框
2. OpenCV—python 图像矫正（基于傅里叶变换—基于透视变换）
3. python 图片中的表格识别
4. OpenCV—Python 表格提取
5. OpenCV—python 形态学处理（腐蚀、膨胀、开闭运算、边缘检测）

1 判断是否需要小角度的旋转

发票中有很多的横线，使用Canny函数获取轮廓+霍夫函数获取直线（这基本上是一个组合拳），然后可以根据这些横线的斜率的均值来确定图像是否有倾斜,以及倾斜之后需要旋转的角度。然后以图像的左下角为坐标中心，完成旋转工作。

import cv2
import numpy as np
import pytesseract
import cv2 as cv
import math

image = cv2.imread('C:\\Users\\14192\\Desktop\\7.jpg', 1)
# 灰度图片
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
edges = cv.Canny(gray, 50, 150, apertureSize=3)  # 50,150,3
cv.imwrite('test_3\\edges_whole.jpg', edges)
lines = cv.HoughLinesP(edges, 1, np.pi / 180, 500, 0, minLineLength=50, maxLineGap=50)  # 650,50,20
print("一共检测到{}条直线".format(len(lines)))
pi = 3.1415
theta_total = 0
theta_count = 0
for line in lines:
    x1, y1, x2, y2 = line[0]
    rho = np.sqrt((x1 - x2) ** 2 + (y1 - y2) ** 2)
    theta = math.atan(float(y2 - y1) / float(x2 - x1 + 0.001))
    print(rho, theta, x1, y1, x2, y2)
    if theta < pi / 4 and theta > -pi / 4:
        theta_total = theta_total + theta
        theta_count += 1
        cv.line(image_copy, (x1, y1), (x2, y2), (0, 0, 255), 2)
        # cv.line(edges, (x1, y1), (x2, y2), (0, 0, 0), 2)
theta_average = theta_total / theta_count
print(theta_average, theta_average * 180 / pi)
cv.imwrite('test_3\\line_detect4rotation.jpg', image_copy)
affineShrinkTranslationRotation = cv.getRotationMatrix2D((0, rows), theta_average * 180 / pi, 1)
gray = cv.warpAffine(gray, affineShrinkTranslationRotation, (cols, rows))
cv.imwrite('test_3\\image_Rotation.jpg', gray)

首先使用Canny函数得到轮廓形状，如下图一所示。然后使用霍夫函数提取到的直线信息(如下图二)，然后通过斜率对直线进行筛选，得到横线的信息（如下图三所示）。

涉及到的图像处理技术

1. Canny轮廓提取

Canny抽取轮廓信息的原理是首先进行高斯去噪，获得平滑图片；
然后获取图像在水平和垂直方向的一阶导数，也就是梯度信息；
接着遍历整图，只保留那些在附近梯度中具有最大梯度的像素点的原始信息，因为很明显的，只有边界上的像素点梯度才是最大的。

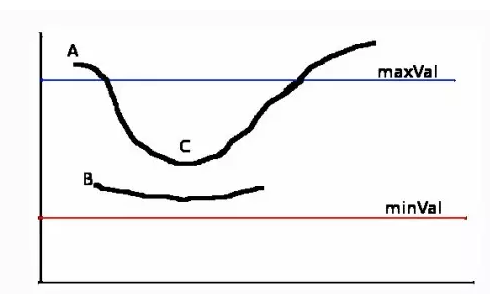
具体怎么选择梯度大小作为阈值也需要人为设置，在Canny函数中有两个阈值要设定，minVal和maxVal.大于maxVal的则被认为是边界，小于minVal则直接抛弃，不认为拥有这样梯度的点是边界。而在两者之间的像素点，则检查其是否和某个边界相连，如果相连，则认为是边界信息，否则抛弃。

下面是一个简单的示意图，参考opencv边缘检测–Canny和机器学习进阶-边缘检测-Canny边缘检测。可以理解，当两个阈值设置的比较小的时候，那么Canny处理之后的图像会保留更多的轮廓信息。在实际使用中，一般需要三个参数，第一个参数是原图img,第二和第三个参数分别是minVal和maxVal,关键字参数apertureSize是计算图像梯度时使用的卷积核的尺寸信息，默认为3，另一关键字参数L2gradient，它可以用来设定求梯度大小的方程，简单使用的时候，可以先不用理会。

2. 霍夫变化获取直线

霍夫变换(Hough Transform)是图像处理中的一种特征提取技术，该过程在一个参数空间中通过计算累计结果的局部最大值得到一个符合该特定形状的集合作为霍夫变换结果。

霍夫变换于1962年由PaulHough首次提出，最初的Hough变换是设计用来检测直线和曲线，起初的方法要求知道物体边界线的解析方程，但不需要有关区域位置的先验知识。这种方法的一个突出优点是分割结果的Robustness,即对数据的不完全或噪声不是非常敏感。然而，要获得描述边界的解析表达常常是不可能的。　后于1972年由Richard Duda & Peter Hart推广使用，经典霍夫变换用来检测图像中的直线，后来霍夫变换扩展到任意形状物体的识别，多为圆和椭圆。霍夫变换运用两个坐标空间之间的变换将在一个空间中具有相同形状的曲线或直线映射到另一个坐标空间的一个点上形成峰值，从而把检测任意形状的问题转化为统计峰值问题。

霍夫线变换是一种用来寻找直线的方法. 在使用霍夫线变换之前, 首先要对图像进行边缘检测的处理，也即霍夫线变换的直接输入只能是边缘二值图像.

在OpenCV中，我们可以用HoughLines函数来调用标准霍夫变换SHT和多尺度霍夫变换MSHT。而HoughLinesP函数用于调用累计概率霍夫变换PPHT。累计概率霍夫变换执行效率很高，所有相比于HoughLines函数，我们更倾向于使用HoughLinesP函数。

lines =cv.HoughLinesP(image, rho, theta, threshold[, lines[, minLineLength[, maxLineGap]]] )

• image：输入图像（必须为二值图像），推荐使用canny边缘检测的结果图像
• rho：累加器的距离分辨率，以像素为单位
• theta：累加器的角度分辨率，以弧度表示
• threshold：累加器阀值参数，int类型，超过设定阈值才被检测出线段，值越大，基本上意味着检出的线段越长，检出的线段个数越少。
• lines：这个参数的意义未知，发现不同的lines对结果没影响，但是不要忽略了它的存在
• minLineLength：检测线段的最小长度
• maxLineGap：同一方向上两条线段判定为一条线段的最大允许间隔（断裂），超过了设定值，则把两条线段当成一条线段，值越大，允许线段上的断裂越大，越有可能检出潜在的直线段

3. 仿射变换

仿射变换是指在向量空间中进行一次线性变换(乘以一个矩阵)并加上一个平移(加上一个向量)，变换为另一个向量空间的过程。在有限维的情况下，每个仿射变换可以由一个矩阵A和一个向量b给出，它可以写作A和一个附加的列b。一个仿射变换对应于一个矩阵和一个向量的乘法，而仿射变换的复合对应于普通的矩阵乘法，只要加入一个额外的行到矩阵的底下，这一行全部是0除了最右边是一个1，而列向量的底下要加上一个1.
Affine Transform描述了一种二维仿射变换的功能，它是一种二维坐标之间的线性变换，保持二维图形的“平直性”(即变换后直线还是直线，圆弧还是圆弧)和“平行性”(其实是保持二维图形间的相对位置关系不变，平行线还是平行线，而直线上的点位置顺序不变，另特别注意向量间夹角可能会发生变化)。仿射变换可以通过一系列的原子变换的复合来实现包括：平移(Translation)、缩放(Scale)、翻转(Flip)、旋转(Rotation)和错切(Shear). 参考资料：opencv学习(三十五)之仿射变换warpAffine

利用opencv实现仿射变换一般会涉及到warpAffine和getRotationMatrix2D两个函数，其中warpAffine可以实现一些简单的重映射，而getRotationMatrix2D可以获得旋转矩阵。

2. 使用opencv对表格的小矩形框进行提取

2.1 图像预处理

# 二值化
binary = cv2.adaptiveThreshold(~gray, 255, cv2.ADAPTIVE_THRESH_GAUSSIAN_C, cv2.THRESH_BINARY, 35, -5)
cv2.imwrite("test4\\gray.jpg", binary)

首先将图片灰度处理，然后使用cv2.adaptiveThreshold实现二值化处理。在灰度图是将原本的三通道转为单通道，每个像素点的值范围在（0,255）之间，0表示黑色，255表示白色。二值化处理则是将图像完全的变成黑白两种颜色(实际会更加复杂)。常用的二值化函数有cv2.threshold固定阈值二值化处理和adaptiveThreshold自适应阈值二值化。固定阈值的方法就是对高于阈值的则统一变为某个指定颜色，低于阈值的则是另一个颜色。自适应阈值二值化函数根据图片一小块区域的值来计算对应区域的阈值，从而得到也许更为合适的图片。参考文章python-opencv函数总结之（一）threshold、adaptiveThreshold、Otsu 二值化

dst = cv2.adaptiveThreshold(src, maxval, thresh_type, type, Block Size, C)

• src： 输入图，只能输入单通道图像，通常来说为灰度图
• dst： 输出图
• maxval： 当像素值超过了阈值（或者小于阈值，根据type来决定），所赋予的值
• thresh_type： 阈值的计算方法，包含以下2种类型：cv2.ADAPTIVE_THRESH_MEAN_C； cv2.ADAPTIVE_THRESH_GAUSSIAN_C.
• type：二值化操作的类型，与固定阈值函数相同，包含以下5种类型： cv2.THRESH_BINARY； cv2.THRESH_BINARY_INV； cv2.THRESH_TRUNC； cv2.THRESH_TOZERO；cv2.THRESH_TOZERO_INV.
• Block Size： 图片中分块的大小
• C ：阈值计算方法中的常数项

在这里输入的图片是~grap这表示逐位取反，所以可以注意到原本白色的变为黑色，原本的深色字体变为白色。

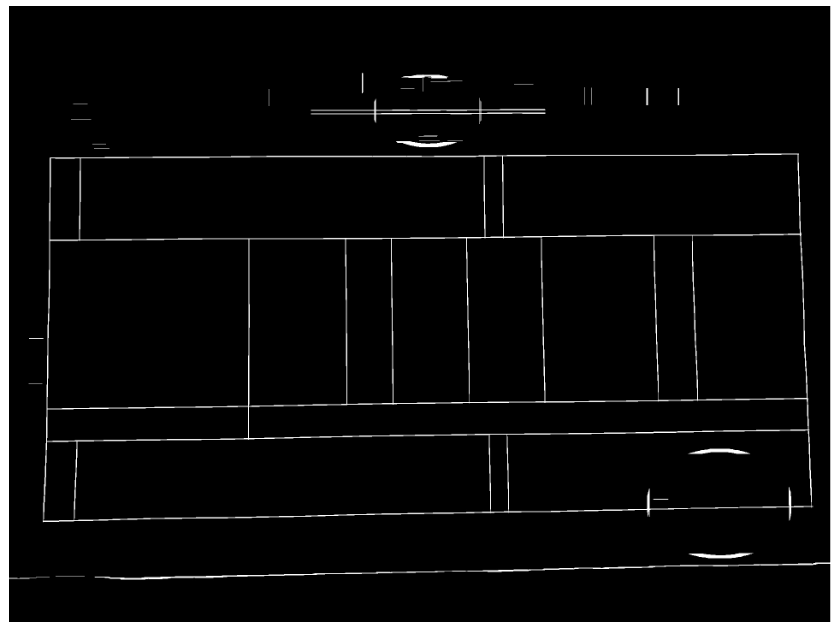
2.2 横竖线识别

根据得到的二值图，分别识别横线、竖线，并将横竖线结合.

rows, cols = binary.shape
print("rows: ", rows, ", cols: ", cols)
scale = 60
# 识别横线
kernel = cv2.getStructuringElement(cv2.MORPH_RECT, (cols // scale, 1))
eroded = cv2.erode(binary, kernel, iterations=1)
cv2.imwrite("test4\\Eroded_Image.jpg", eroded)
dilatedcol = cv2.dilate(eroded, kernel, iterations=1)
cv2.imwrite("test4\\transverse.jpg", dilatedcol)

# 识别竖线
scale = 20
kernel = cv2.getStructuringElement(cv2.MORPH_RECT, (1, 40))
eroded = cv2.erode(binary, kernel, iterations=1)
dilatedrow = cv2.dilate(eroded, kernel, iterations=1)
cv2.imwrite("test4\\verticalline.jpg", dilatedrow)

# 标识交点
bitwiseAnd = cv2.bitwise_and(dilatedcol, dilatedrow)
#  cv2.imshow("表格交点展示：", bitwiseAnd)
cv2.imwrite("test4\\point.jpg", bitwiseAnd)  # 将二值像素点生成图片保存
print(bitwiseAnd.shape)

merge = cv2.add(dilatedcol, dilatedrow)

这里或许会有这样的疑惑，既然上面提到的霍夫函数可以用来提取直线，那么为什么这里不使用。我的感觉是，当需要寻找大尺度直线的时候，可以使用霍夫函数。但是对于这种全局的含有各种小线段的图像，就不合适了，首先霍夫函数需要手动的设置阈值，只有超过阈值的才会被认为是直线。我们可以做一个简单实验，下面是阈值为col/20,col/10,col/7,col/5的不同结果。可以看到根本无法得到我们需要的边框线。

因此需要使用腐蚀和膨胀。识别横线和竖线的原理都是一样，通过设置相应的核矩阵kernel，然后进行腐蚀eroded和膨胀操作dilate。这样就可以得到横竖线。横竖线的交点可以通过bitwise_and函数获得，横竖线的交叉图像可以通过add函数实现。

涉及到的图像处理技术

这里主要要介绍一下核矩阵以及腐蚀、膨胀、开运算、闭运算，其他的形态选处理可以参考形态学处理（腐蚀、膨胀、开闭运算、边缘检测）

核矩阵本质是一个np.array的数组，比如一个十字核矩阵

element = cv2.getStructuringElement(cv2.MORPH_CROSS,(5,5))

其本质是一个这样的矩阵

array([[0, 0, 1, 0, 0],
       [0, 0, 1, 0, 0],
       [1, 1, 1, 1, 1],
       [0, 0, 1, 0, 0],
       [0, 0, 1, 0, 0]], dtype=uint8)

同理可以知道

cv2.getStructuringElement(cv2.MORPH_RECT,(5,5))

其本质是全1矩阵。

我们定义了一个这样的核矩阵之后，就使用他来进行腐蚀和膨胀操作。

• 腐蚀：腐蚀会把物体的边界腐蚀掉，卷积核沿着图象滑动，如果卷积核对应的原图的所有像素值为1，那么中心元素就保持原来的值，否则变为零。主要应用在去除白噪声，也可以断开连在一起的物体。
• 膨胀：卷积核所对应的原图像的像素值只要有一个是1，中心像素值就是1。一般在除噪是，先腐蚀再膨胀，因为腐蚀在去除白噪声的时候也会使图像缩小，所以我们之后要进行膨胀。当然也可以用来将两者物体分开。

我们这里使用的核矩阵形状为(cols // scale, 1)，对于上图的发票，其col为1920，scale人为设置成40，也就是(48,1)，这是一个长条形的全1矩阵，那么这个矩阵在用于腐蚀的时候， 会将长直线保留，而距离短于48像素的类横线则会被覆盖为黑色。这样就不用担心文字中的横线会被保留下来。膨胀的原理也类似，不做赘述了。腐蚀和膨胀的返回结果依旧是原图大小的image，如上图所示。

开运算和闭运算是将腐蚀和膨胀按照一定的次序进行处理。但这两者并不是可逆的，即先开后闭并不能得到原先的图像。

为了获取图像中的主要对象：对一副二值图连续使用闭运算和开运算，或者消除图像中的噪声，也可以对图像先用开运算后用闭运算，不过这样也会消除一些破碎的对象。

• 开运算：先腐蚀后膨胀，用于移除由图像噪音形成的斑点。
• 闭运算：先膨胀后腐蚀，用来连接被误分为许多小块的对象；

2.3 表格划分

在获得了横线和竖线的交点图像bitwiseAnd以及获得横线和竖线的交叉图像merge之后，关于如何划分表格，主要有两种不同的思路

1. 使用opencv的findContours()功能获得矩形轮廓
2. 根据交点，删除多余的交点之后，一次遍历其交点进行切分

我使用的是第一种思路，先把代码附上，后面会说第二种思路的适用场景。

def get_contours(image):
    image_copy = image
    rows,cols =image.shape
    contours, hierarchy = cv.findContours(image, cv.RETR_LIST, cv.CHAIN_APPROX_SIMPLE)
    length = len(contours)
    print("找到{}个轮廓".format(length))
    rects = []

    for i in range(length):
        cnt = contours[i]
        area = cv.contourArea(cnt)
        if area < int(rows*cols*0.001):
            continue
        approx = cv.approxPolyDP(cnt, 3, True)  # 3
        x, y, w, h = cv.boundingRect(approx)
        rect = (x, y, w, h)
        small_rects.append(rect)
        # cv.rectangle(image_copy, (x, y), (x+w, y+h), (0, 0, 255), 3)
        # cv.imwrite('test1\\table_out.jpg', image_copy)
        roi = image[y:y + h, x:x + w]
        joints_contours, joints_hierarchy = cv.findContours(roi, cv.RETR_LIST, cv.CHAIN_APPROX_SIMPLE)
        # print len(joints_contours)
        # if h < 80 and h > 20 and w > 10 and len(joints_contours)<=4:
        if h < 80 and h > 20 and w > 10 and len(joints_contours) <= 6:  # important
            cv.rectangle(image_copy, (x, y), (x + w, y + h), (255 - h * 3, h * 3, 0), 3)
            # small_rects.append(rect)
    cv.imwrite('test4\\table_out.jpg', image_copy)
    print("经过筛选之后，留下{}个轮廓".format(len(small_rects)))
    return small_rects
    
small_rects = get_contours(merge1)

通过上面的代码，可以获得每个表格框了，如果切分一下，得到的结果如下：

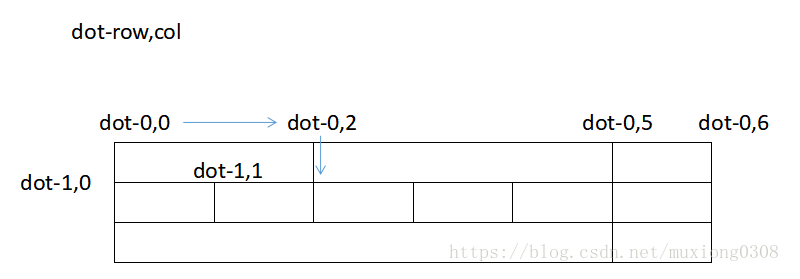
第二种思路，关于交点的使用方式，也有两种思路。首先参考 要点初见：Python+OpenCV校正并提取表格中的各个框中的代码，使用了第一种方式，这种方式的思路是通过获得的交点图像，将其中白色交叉点的坐标提取出来；删除坐标位置很近的冗余坐标；将横纵坐标排序之后，分别保存在两个列表中，然后依次遍历纵坐标、横坐标，两重循环的方式进行切割。

for i in range(len(mylisty) - 1):
    for j in range(len(mylistx) - 1):
        # 在分割时，第一个参数为y坐标，第二个参数为x坐标
        ROI = image[mylisty[i] + 3:mylisty[i + 1] - 3, mylistx[j]:mylistx[j + 1] - 3]  # 减去3的原因是由于我缩小ROI范围
        cv2.imwrite("test1//fengezituzhanshi{}{}.jpg".format(i,j), ROI)

这种方式适用于excel那种比较标准的表格。如下图所示，而对于发票这种则会导致多余的切割。

第二种思路的另一个实现可以用下面的图来表示，我没有尝试实现，但是应该是可行的。

备忘

1. 粗线段如何识别为细线段问题