[人工智能]32李沐动手学深度学习v2/批量归一化 mini-batch normalization

$u_B=\frac{1}{B}\sum _{i\in B}{x}_i$

${\sigma }_B^2=\frac{1}{|B|}\sum _{i\in B}(x_i?u_B{)}^2+?$, $?$ 是1个很小的数，防止方差为0

$x_{i+1}=\gamma \frac{x_i?{\hat{\mu }}_B}{{\hat{\sigma }}_B}+\beta$, B is mini_batch_data, $\gamma$是需要学习的方差, $\beta$是需要学习的期望, ${\hat{\mu }}_B$ is mean, ${\hat{\sigma }}_B$ is var,

import torch
from torch import nn
from d2l import torch as d2l

def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):
    '''
    mini_batch_norm
    :param X 这个层的输入
    :param gamma 需要学习的方差
    :param beta 需要学习的期望
    :param moving_mean 整个数据集的期望，不是这个小批量数据的期望，做推理时使用
    :param moving_var 整个数据集的方差，不是这个小批量数据的方差，做推理时使用
    :param eps 有常用值，每个框架都不同，通常取1e-5
    :param momentum 用于更新moving_mean和moving_var，有常用值，每个框架都不同，通常取0.9
    '''
    # 做推理的时候
    # 没有开启梯度计算
    if not torch.is_grad_enabled():
        # 为什么仅仅使用全局的均值和全局方差，做推理可能就1张图片，没有批量的概念
        X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
    else:
        # x必须等于2或者4
        # x=2，全连接层
        # x=4，二维卷积层
        assert len(X.shape) in (2, 4)
        # x=2，全连接层，对特征求均值和方差
        if len(X.shape) == 2:
            # 默认，按那一维求均值，那一个维度消失
            # 按第0维求均值，求每个特征的均值，作用在每个特征上
            # ！按第0维求均值，运算作用在第2维上
            # mean.shape=1xn
            mean = X.mean(dim=0)
            # 求两个样本的方差
            var = ((X - mean) ** 2).mean(dim=0)
        # x=4，二维卷积层，对通道求均值和方差
        else:
            # 保留维度
            # 0维，批量大小。1维，前一层输出通道数。2维，高。3维，宽
            # ！按第0维，2维，3维，求均值，运算作用在第1维上
            # 1xnx1x1 四维
            mean = X.mean(dim=(0, 2, 3), keepdim=True)
            var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True)
        # mean和var都是在当前mini_batch_data中求出的均值和方差
        # X_hat=1xnx1x1
        X_hat = (X - mean) / torch.sqrt(var + eps)
        moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
        moving_var = momentum * moving_var + (1.0 - momentum) * var
    # beta，直接把入参加入进来了
    # moving_mean和moving_var只在推理的时候有用，训练的时候没用
    # gamma.shape=beta.shape=1xnx1x1
    Y = gamma * X_hat + beta
    return Y, moving_mean.data, moving_var.data

class BatchNorm(nn.Module):
    '''
    BatchNorm层
    '''
    def __init__(self, num_features, num_dims):
        '''
        :param num_features=2，特征量。num_features=4，前1层输出通道数
        :param num_dims=2，全连接层。num_dims=4，二维卷积层
        '''
        super().__init__()
        if num_dims == 2:
            shape = (1, num_features)
        else:
            shape = (1, num_features, 1, 1)
        # 全1初始化需要学习的方差，如果全0，在公式中乘之后全0
        self.gamma = nn.Parameter(torch.ones(shape))
        # 全0初始化需要学习的均值
        self.beta = nn.Parameter(torch.zeros(shape))
        # 全1初始化整个数据集的方差
        self.moving_var = torch.ones(shape)
        # 全0初始化整个数据集的期望
        self.moving_mean = torch.zeros(shape)

    def forward(self, X):
        # 小批量数据X和整体数据均值要放到同一设备上
        if self.moving_mean.device != X.device:
            self.moving_mean = self.moving_mean.to(X.device)
            self.moving_var = self.moving_var.to(X.device)
        Y, self.moving_mean, self.moving_var = batch_norm(
            X, self.gamma, self.beta, self.moving_mean,
            self.moving_var, eps=1e-5, momentum=0.9)
        return Y

应用BatchNorm 于LeNet模型

net = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5),
    # 6二维卷积层的输出通道数。num_dims=4 表示作用于二维卷积层的输出通道上
    BatchNorm(6, num_dims=4), 
    nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), 
    # 16二维卷积层的输出通道数。num_dims=4 表示作用于二维卷积层的输出通道上
    BatchNorm(16, num_dims=4), 
    nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2), 
    nn.Flatten(),
    nn.Linear(16*4*4, 120), BatchNorm(120, num_dims=2), 
    nn.Sigmoid(),
    nn.Linear(120, 84), 
    # 84特征量。num_dims=2 表示作用于全连接层的特征上
    BatchNorm(84, num_dims=2), 
    nn.Sigmoid(),
    nn.Linear(84, 10))

在Fashion-MNIST数据集上训练网络

lr, num_epochs, batch_size = 1.0, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

loss 0.270, train acc 0.900, test acc 0.796
25335.7 examples/sec on cuda:0

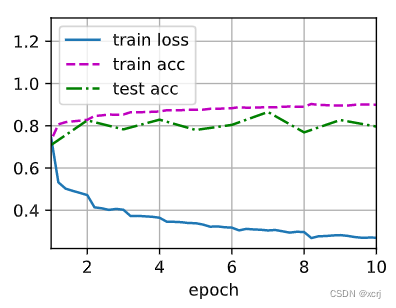
# 查看net第1层（batchNorm层）的参数，方差学习参数gamma和均值学习参数beta
net[1].gamma.reshape((-1,)), net[1].beta.reshape((-1,))

(tensor([2.4066, 2.6878, 3.8948, 0.4407, 2.3572, 4.0047], device='cuda:0',
        grad_fn=<ReshapeAliasBackward0>),
 tensor([ 0.6224,  0.5743, -3.8525,  0.8712,  2.7259, -2.4347], device='cuda:0',
        grad_fn=<ReshapeAliasBackward0>))

简洁实现

net = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5), 
    # 6输出通道数
    nn.BatchNorm2d(6), 
    nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), 
    # 16输出通道数
    nn.BatchNorm2d(16), 
    nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2), 
    nn.Flatten(),
    nn.Linear(256, 120), 
    # 120特征量
    nn.BatchNorm1d(120), 
    nn.Sigmoid(),
    nn.Linear(120, 84), 
    # 84特征量
    nn.BatchNorm1d(84), 
    nn.Sigmoid(),
    nn.Linear(84, 10))

使用相同超参数来训练模型

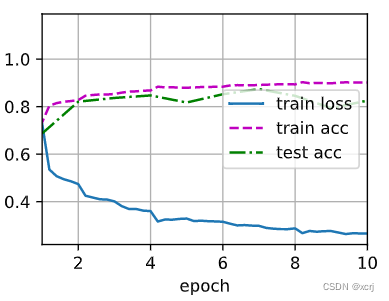
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

loss 0.266, train acc 0.902, test acc 0.826
48070.5 examples/sec on cuda:0

总结

• 批量归一化的作用：学习输入层的时候，输入层改变时，避免变化输出层
• 批量归一化的作用：网络层输入数据的稳定性
• 批量归一化固定小批量中的均值和方差，学习出合适的缩放gamma和偏移mean
• 全连接层》批量归一化（作用在全连接层的特征上）》激活函数
• 卷积层》批量归一化（作用在卷积层的输出通道上）》激活函数
• 全连接层》批量归一化》激活函数》不使用丢弃层了

query
一旦模型稳定了，收敛就不会变慢

数值稳定性：

• 合理的权重初始化
• 合理的激活函数
• 归一化：batch normalization
• 网络架构：乘法变加法

！！！数值稳定性：

• 答：数值稳定性作用，防止梯度消失和梯度爆炸，保证正向每层输出的稳定性和反向梯度的稳定性
• 答：权重初始化作用，训练开始时数值稳定性，保证训练开始时输出的稳定性，不能保证训练中输出的稳定性
• 答：使用靠近y=x的激活函数作用，保证正向每层输出的稳定性和反向梯度的稳定性
• 答：归一化作用，训练中数值稳定性，训练中网络层输入数据的稳定性

MLP中可以用batch normalization

• 答：不适用于浅层神经网络，深度越深越能体现优势

batch normalization

• 答：也是线性变换，相当于线性层，缩放和偏移

batch normalization收敛时间变短

• 答：梯度变化，梯度稳定，可以使用更大的学习率进行训练，权重的更新变快

调参num_epochs, batch_size, lr,

• 答：三者相互关联
• 答：num_epochs大一些没关系，顶多浪费一些资源，不再收敛可以停掉，下次直到要设定的合适值了
• 答：batch_size需要调整到合适大小，batch_size增大后每秒处理的样本数没有变化则找到合适值了，根据你的内存+gpu计算快的数值
• 答：lr

xxx normalization

• 答：网上有好的对比图，normalization发生在什么地方
• 答：https://blog.csdn.net/u013289254/article/details/99690730