为了准确和及时预测局部区域的降雨及温度,提出了一种基于
Attention和LSTM组合模型(ALSTM) 的关联多值预测算法。该算法利用天气时间序列中 的前期数据,对下一小时的降雨量和温度进行关联预测,以此实现对天气要素的多值预测。该算法首先对输入数据进行归一化处理; 然后利用数据对ALSTM 模型进行训练; 最后将训练好的模型用于多值预测。
涉及:LSTM Attention机制 多变量
创新点
- ① 区别于传统方法及浅层神经网络方法,该算法采用递归神经网络中的长短期记忆模型( long short-term memory,LSTM)
形成深度循环神经网络,可从历史天气数据中,提取其深层特征,对未来的降雨和温度进行预测,取得了更好的预测结果; - ②将 LSTM 模型与 Attention 机制结合,使之更注重数据中的一些重要特征,从而提高了预测多目标数值的稳定性和正确率;
- ③将两个或多个LSTM模型进行
堆叠组合,将前一个模型的输出作为下一个模型的输入,这样可在同一模型中同时预测两个或多个关联值,这样更满足短时天气预测的需求。
雷达预测,气象卫星皆存在其局限性,神经网络快速发展,也想来凑凑热闹。
LSTM模型在这里就不过多介绍了,有需要了解的小伙伴可以去看博主关于LSTM的学习记录。
模型介绍
Attention 模型
Attention 模型最初被用于机器翻译,现在已被广泛运用于机器学习以及和许多神经网络模型相结合中。
简单的说,注意力机制类似于人去看一个图画,注意力往往会根据个人喜好的不同而对图画中某一区域,注入更多的注意力,即更倾向于关注图像中的部分重要信息。在 RNN 中,结合注意力机制可以使某些重要的因素更容易被捕获,数据内部逻辑结构的相关性也更容易被建模起来,这解决了因为处
理长序列输入而导致等待时间过久,权重分配不当的问题,从而提高预测性能。
传统编码器 解码器结构 如图 2 所示。输入序列( x1,x2,…,xt ) ,被 RNN 编码器编码为固定长度的向量( h1,h2,…,ht ) ,其中 t 表示输入序列长度。解码器通过已经编码过后的序列结合状态( s1,s2,…,st) 生成一个输出序列( y1,y2,…,yt ) ,其中 t 表示输出序列长度。在此编码过程中的 ht以及解码过程中的 st 都表示不同解码器的隐状态。
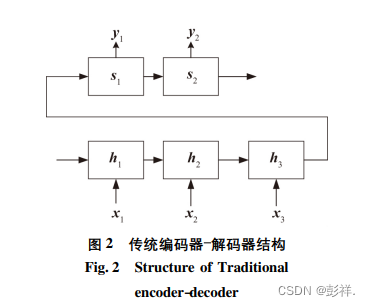
注意力机制的相应编码器 解码器体系结构如图 3 所示。注意力权重 αij 在编码过程中自动学习,并自动捕获 hi 和 sj ,其隐状态的相关性也在此过程中被发现,此后,注意力机制构建内容向量 c ,即分配更精准的注意力权重。该权重用于构建解码过程中的 sj 和编码过程中的 hi 更合理的转换,其中内
容向量 cj 是编码器所有隐状态及其相应注意力权重相乘的加权和,其计算公式如下:
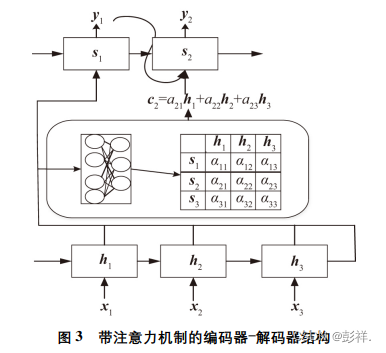
注意力机制的加入类似于前馈神经网络。而与前馈网络不同的是,注意力机制在学习过程中学习一个特殊的注意力权重 αij,以此构建 hi 和 sj-1 的转换函数。
ALSTM 模型
在气象研究问题中,气温和降雨存在着相关性,但是现存的神经网络模型往往只能预测某一短期天 气数值。为了预测多个天气数值,将 LSTM
神经网络堆叠形成深度关联循环神经网络,将第一个输出值 作为第二个预测值的输入; 并在此基础上加入 Attention 机制,因而得到了基于
Attention 和 LSTM 组合的多值预测模型( ALSTM) 。ALSTM 模型结构如图 4 所示。
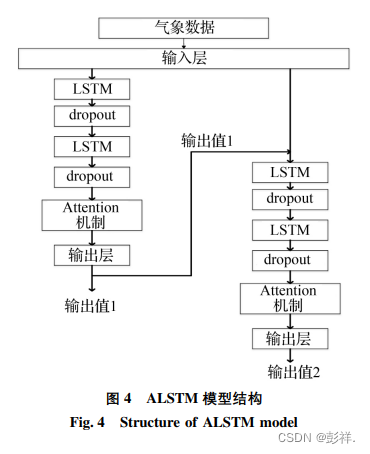
ALSTM 模型的数据流程如图 5 所示。在训练开始时,天气数据通过输入层同时进入两个分支,这两个分支分别预测空气温度和降雨,模型在预测空气温度后将其作为预测降雨的输入参数,以此产生多值关联预测。
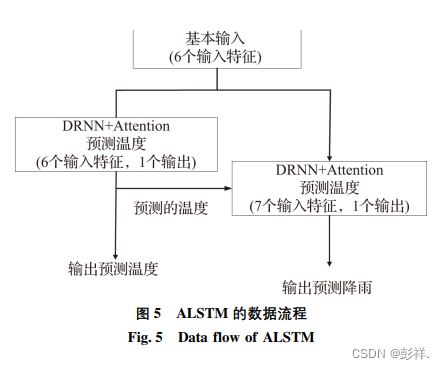
在模型的训练阶段中,总误差 Ltotle 用来作为模型预测结果的评估,训练阶段的目标是获取最小的总误差,总误差的计算公式如下:
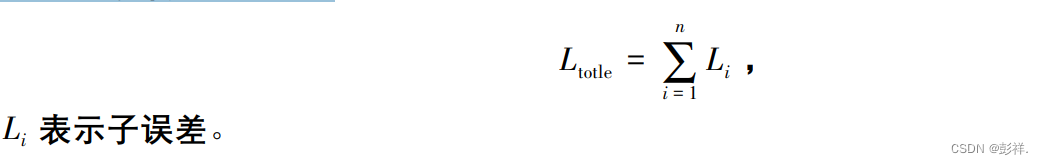
参数设计和算法设计
参数设计
在传统的 LSTM 神经网络输入中有一个步长参数,表示预测值与多少历史数据有关。为了在ALSTM模型的实验中使用较好的步长,采用 10000 个样本数据,步长分别为 3、5、10、20,迭代次数为 50
次进行对比实验,平均误差变化分别如图所示:

选定不同步长时,收敛速度相差不大,但在选定步长为 10 时,下降曲线较为平缓。故选取步长 10 作为 ALSTM 模型的步长。
算法设计
本文所采用的算法建立在深度学习的基础上,将 Adam 算法作为梯度下降的算法,ALSTM 的步长设置为 10,神经元个数设置为 300,模型学习率为 0. 0006,dropout 层定义为 0. 99 的损失比。深度学习通常需要大量的时间和计算资源来训练。因此需要找到一种资源少、收敛速度快的优化算法,而 Adam 优化算法在求解非凸优化问题上具有很大的优势,它的本质是对随机梯度下降算法的扩展。
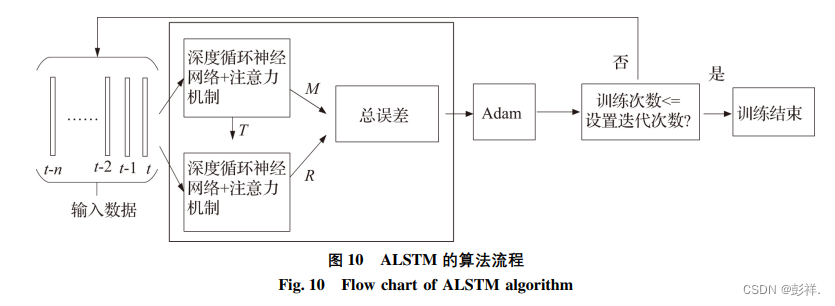
算法在训练阶段,将 Ltotle 做为算法的评价函数,算法包含两个关联的 DRNN 网络。具体的算法步骤如下:
Step 1: 接受输入,通过正则化函数将数据归一化,温度和累计雨量作为第一个预测输出和第二个预测输出。
Step 2: 设置每轮训练数量为 500 个,训练次数为 100 次,建立 LSTM 接收输入,激活函数为 relu 函数,加入 Attention 机制,为其分配权重,最后的输出变成了注入 Attention 机制的加权求和温度值,得到第一个温度误差 M 以及第一个预测的空气温度值 T。
Step 3: 根据已经正则化的输入以及预测的空气温度值,再次利用 ALSTM 模型去预测降雨值,得到第二个降雨误差值 R 和预测降雨量 P。
Step 4: 根据两个误差值相加得到总误差值 Ltotle ,然后利用 Adam 算法对总误差之进行优化,将总误差值降低,如果总误差值没有变化或者当达到训练迭代次数时,算法结束。
实验结果和分析
在本文算法实验中,采用均方误差( mean absolute error,MSE) 作为训练阶段计算训练偏差程度的评价指标,因 MSE 是参数的估计值与参数的真值之差的平方的期望值,能更好地反应模型对数据的拟合情况,其值用字母 E 表示,计算公式如下:
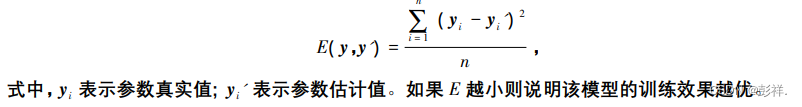
测试阶段的实验分析
为了验证模型的预测效果,采用测试数据集对模型进行了验证,测试数据按照时间顺序排列。在本实验中,采用绝对误差( mean absolute error,MAE) 作为计算偏差程度的评价指标,能更好地反映预测值与真实值存在的误差的真实情况,并用 1 - MAE 的结果作为模型的精度评价指标。用字母 A 表示 MAE的大小,计算公式如下:
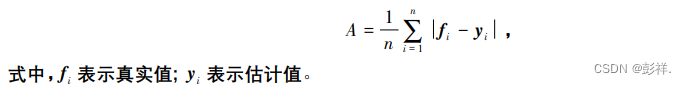
结论
本文提出了 ALSTM 预测算法。给出了 ALSTM 的模型结构、算法框架设计,并将 ALSTM 算法与 LSTM、BP 和 DRNN 网络算法进行了性能对比实验。通过 4 种算法在温度和降雨方面的预测结果对 比,验证了 ALSTM 模型的准确性及可行性。实验结果表明,ALSTM模型不仅优于其他 3 种神经网络模 型,并且还能同时预测两个天气数值,且平均精度在 97 %以上。这也说明了天气数据相互之间存在关 联性。但 ALSTM 仍存在一些有待改进的地方,例如在训练阶段使用简单的算术平均算法来计算总误差,目标是通过减少总误差来优化模型。这种误差计算方法没有考虑各个误差之间的关系,也没有考虑总误差最小时的一些细节,如各子误差的极端情况和误差减少过程中的振荡。下一步,我们将研究输入参数的优化,以及输入参数之间的关系,以提高模型的平均精度。相信在不久的将来,更准确的天气数 据将能被人们所预测。