[人工智能]基于文心NLP大模型的阅读理解可解释评测过程记录2

链接：Tensor介绍-使用文档-PaddlePaddle深度学习平台

Tensor

概念

Tensor（张量），表示神经网络中传递的数据，可以理解为多维数组。

优势

1、与 Numpy 数组相比，Tensor 除了支持运行在 CPU 上，还支持运行在 GPU 及各种 AI 芯片上，以实现计算加速；

2、飞桨基于 Tensor，实现了深度学习所必须的反向传播功能和多种多样的组网算子，从而可更快捷地实现深度学习组网与训练等功能。

代码

def train(model):
    model.train()
    epochs = 2
    optim = paddle.optimizer.Adam(learning_rate=0.001, parameters=model.parameters())
    # 模型训练的两层循环
    for epoch in range(epochs):
        for batch_id, data in enumerate(train_loader()):
            x_data = data[0]
            y_data = data[1]
            print("x_data: ", x_data[0][0][0][0]) # 打印神经网络的输入：批数据中的第一个数据的第一个元素
            predicts = model(x_data)
            print("predicts: ", predicts[0]) # 打印神经网络的输出：批数据中的第一个数据的第一个元素
            print("weight: ", model.linear1.weight[0][0]) # 打印神经网络的权重：linear1层的weight中的第一个元素
            loss = F.cross_entropy(predicts, y_data)
            acc = paddle.metric.accuracy(predicts, y_data)
            loss.backward()
            optim.step()
            optim.clear_grad()
            break
        break
model = LeNet()
train(model)

相关函数

1、model.train()

【Pytorch】model.train() 和 model.eval() 原理与用法_想变厉害的大白菜的博客-CSDN博客_model.train() pytorch

2、?paddle.optimizer提供优化器算法相关API

pytorch中model.parameters()函数_Sinsinw的博客-CSDN博客_model.parameters()

创建

使用?paddle.to_tensor?创建任意维度的 Tensor

（1）创建类似向量（vector）的 1 维 Tensor

import paddle # 后面的示例代码默认已导入 paddle 模块
ndim_1_Tensor = paddle.to_tensor([2.0, 3.0, 4.0])
print(ndim_1_Tensor)

结果：

特殊地，如果仅输入单个标量（scalar）数据（例如 float/int/bool 类型的单个元素），则会创建形状为 [1] 的 Tensor，即 0 维 Tensor：

#两种创建方式完全一样
p1=paddle.to_tensor(2)
p2=paddle.to_tensor([2])
print(p1)
print(p2)

?结果：?

（2）创建类似矩阵（matrix）的 2 维 Tensor

ndim_2_Tensor = paddle.to_tensor([[1.0, 2.0, 3.0],
                                  [4.0, 5.0, 6.0]])
print(ndim_2_Tensor)

结果：

shape=【行，列】，dtype：数据类型

（3）创建 3 维 Tensor

ndim_3_Tensor = paddle.to_tensor([[[1, 2, 3, 4, 5],
                                   [6, 7, 8, 9, 10]],
                                  [[11, 12, 13, 14, 15],
                                   [16, 17, 18, 19, 20]]])
print(ndim_3_Tensor)

结果：?

ndim_3_Tensor = paddle.to_tensor([[[1, 2, 3, 4, 5],
                                   [6, 7, 8, 9, 10]],
                                  [[11, 12, 13, 14, 15],
                                   [16, 17, 18, 19, 20]]])
print(ndim_3_Tensor)

可视化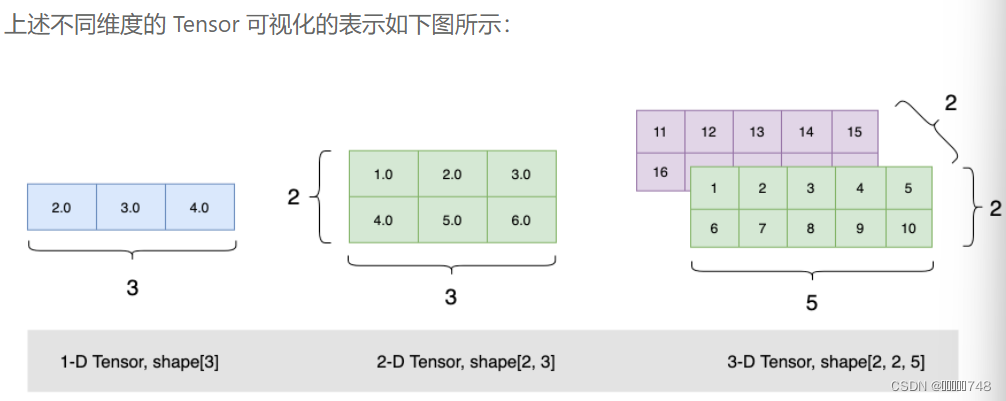

?

注意

Tensor 必须形如矩形，即在任何一个维度上，元素的数量必须相等，否则会抛出异常

(4）?创建指定形状

paddle.zeros([m, n])             # 创建数据全为 0，形状为 [m, n] 的 Tensor
paddle.ones([m, n])              # 创建数据全为 1，形状为 [m, n] 的 Tensor
paddle.full([m, n], 10)          # 创建数据全为 10，形状为 [m, n] 的 Tensor

结果：

?

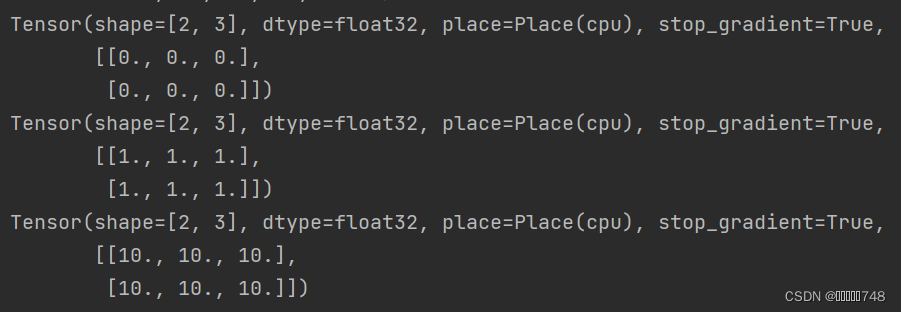
（5） 创建指定区间

print(paddle.arange(0, 10, 2)) # 创建以步长step均匀分隔区间[start, end)的Tensor
print(paddle.linspace(0, 10, 5))# 创建以元素个数num均匀分隔区间[start, end)的Tensor

结果：

?

（6）创建指定图像、文本数据

• 对于图像场景，可使用?paddle.vision.transforms.ToTensor?直接将 PIL.Image 格式的数据转为 Tensor，使用?paddle.to_tensor?将图像的标签（Label，通常是Python 或 Numpy 格式的数据）转为 Tensor。

• 对于文本场景，需将文本数据解码为数字后，再通过?paddle.to_tensor?转为 Tensor。不同文本任务标签形式不一样，有的任务标签也是文本，有的则是数字，均需最终通过 paddle.to_tensor 转为 Tensor。

import numpy as np
from PIL import Image
import paddle.vision.transforms as T
import paddle.vision.transforms.functional as F

fake_img = Image.fromarray((np.random.rand(224, 224, 3) * 255.).astype(np.uint8)) # 创建随机图片
transform = T.ToTensor()
tensor = transform(fake_img) # 使用ToTensor()将图片转换为Tensor
print(tensor)

结果：

?

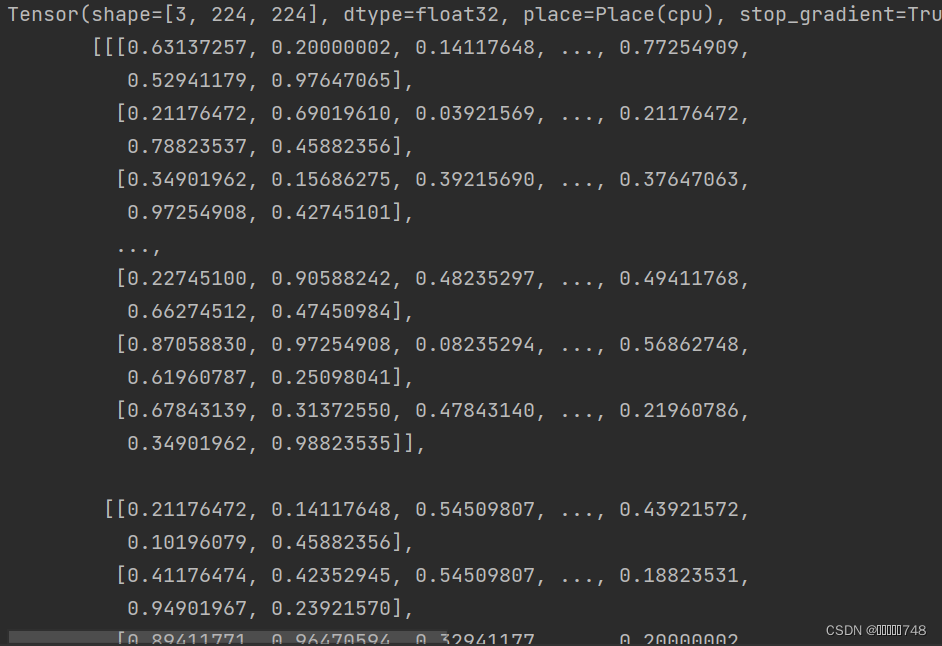
（7）其他创建方式

• 创建一个空 Tensor，即根据 shape 和 dtype 创建尚未初始化元素值的 Tensor，可通过?paddle.empty?实现。

• 创建一个与其他 Tensor 具有相同 shape 与 dtype 的 Tensor，可通过?paddle.ones_like?、?paddle.zeros_like?、?paddle.full_like?、paddle.empty_like?实现。

• 拷贝并创建一个与其他 Tensor 完全相同的 Tensor，可通过?paddle.clone?实现。

• 创建一个满足特定分布的Tensor，如?paddle.rand,?paddle.randn?,?paddle.randint?等。

• 通过设置随机种子创建 Tensor，可每次生成相同元素值的随机数 Tensor，可通过?paddle.seed?和?paddle.rand?组合实现。

属性

shape

1）介绍

Tensor(shape=[3], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [2., 3., 4.])

• shape：描述了 Tensor 每个维度上元素的数量。

• ndim： Tensor 的维度数量，例如向量的维度为 1，矩阵的维度为2，Tensor 可以有任意数量的维度。

• axis 或者 dimension：Tensor 的轴，即某个特定的维度。

• size：Tensor 中全部元素的个数。

?

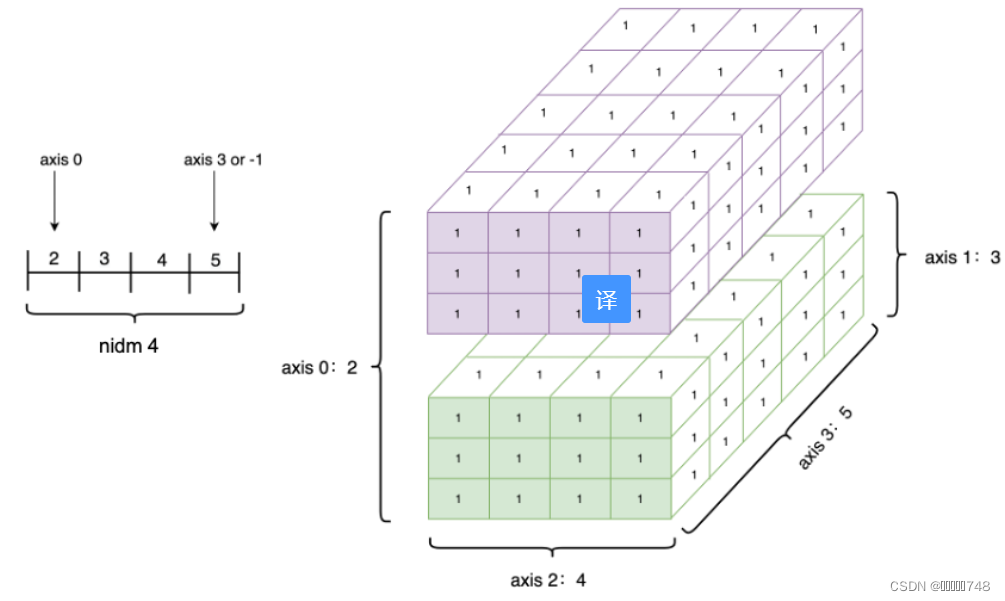
2）重置?

1、reshape

创建 1 个?shape=[3]?的一维 Tensor，使用 reshape 功能将该 Tensor 重置为?shape=[1,?3]?的二维 Tensor。这种做法经常用在把一维的标签（label）数据扩展为二维，由于飞桨框架中神经网络通常需要传入一个 batch 的数据进行计算，因此可将数据增加一个 batch 维，方便后面的数据计算。

ndim_1_Tensor = paddle.to_tensor([1, 2, 3])
print("the shape of ndim_1_Tensor:", ndim_1_Tensor.shape)

reshape_Tensor = paddle.reshape(ndim_1_Tensor, [1, 3])
print("After reshape:", reshape_Tensor.shape)

结果：

?技巧：

• -1?表示这个维度的值是从 Tensor 的元素总数和剩余维度自动推断出来的。因此，有且只有一个维度可以被设置为 -1。

• 0?表示该维度的元素数量与原值相同，因此 shape 中 0 的索引值必须小于 Tensor 的维度（索引值从 0 开始计，如第 1 维的索引值是 0，第二维的索引值是 1）。

origin:[3, 2, 5] reshape:[3, 10]      actual: [3, 10] # 直接指定目标 shape
origin:[3, 2, 5] reshape:[-1]         actual: [30] # 转换为1维，维度根据元素总数推断出来是3*2*5=30
origin:[3, 2, 5] reshape:[-1, 5]      actual: [6, 5] # 转换为2维，固定一个维度5，另一个维度根据元素总数推断出来是30÷5=6
origin:[3, 2, 5] reshape:[0, -1]         actual: [3, 6] # reshape:[0, -1]中0的索引值为0，按照规则，转换后第0维的元素数量与原始Tensor第0维的元素数量相同，为3；第1维的元素数量根据元素总值计算得出为30÷3=10。
origin:[3, 2] reshape:[3, 1, 0]          error： # reshape:[3, 1, 0]中0的索引值为2，但原Tensor只有2维，无法找到与第3维对应的元素数量，因此出错。

2、其他方法

• paddle.squeeze，可实现 Tensor 的降维操作，即把 Tensor 中尺寸为 1 的维度删除。

• paddle.unsqueeze，可实现 Tensor 的升维操作，即向 Tensor 中某个位置插入尺寸为 1 的维度。

• paddle.flatten，将 Tensor 的数据在指定的连续维度上展平。

• transpose，对 Tensor 的数据进行重排。

3）原位和非原位操作

原位操作即在原 Tensor 上保存操作结果，输出 Tensor 将与输入Tensor 共享数据，并且没有 Tensor 数据拷贝的过程。非原位操作则不会修改原 Tensor，而是返回一个新的 Tensor。通过 API 名称区分两者，如?paddle.reshape?是非原位操作，paddle.reshape_?是原位操作。

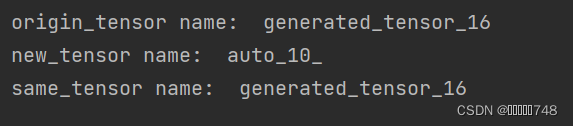
origin_tensor = paddle.to_tensor([1, 2, 3])
new_tensor = paddle.reshape(origin_tensor, [1, 3]) # 非原位操作
same_tensor = paddle.reshape_(origin_tensor, [1, 3]) # 原位操作
print("origin_tensor name: ", origin_tensor.name)
print("new_tensor name: ", new_tensor.name)
print("same_tensor name: ", same_tensor.name)

结果：

数据类型

1）介绍

• 对于 Python 整型数据，默认会创建?int64?型 Tensor；

• 对于 Python 浮点型数据，默认会创建?float32?型 Tensor，并且可以通过?paddle.set_default_dtype?来调整浮点型数据的默认类型。

• Tensor 不仅支持 float、int 类型数据，也支持 complex 复数类型数据。如果输入为复数，则 Tensor 的 dtype 为?complex64?或?complex128?，其每个元素均为 1 个复数。如果未指定，默认数据类型是complex64：

2）修改

float32_Tensor = paddle.to_tensor(1.0)

float64_Tensor = paddle.cast(float32_Tensor, dtype='float64')
print("Tensor after cast to float64:", float64_Tensor.dtype)

int64_Tensor = paddle.cast(float32_Tensor, dtype='int64')
print("Tensor after cast to int64:", int64_Tensor.dtype)

结果：

?

设备位置

初始化 Tensor 时可以通过?Tensor.place?来指定其分配的设备位置。

可支持的设备位置有：CPU、GPU、固定内存、XPU（Baidu Kunlun）、NPU（Huawei）、MLU（寒武纪）、IPU（Graphcore）等。

其中固定内存也称为不可分页内存或锁页内存，其与 GPU 之间具有更高的读写效率，并且支持异步传输，这对网络整体性能会有进一步提升，但其缺点是分配空间过多时可能会降低主机系统的性能，因为其减少了用于存储虚拟内存数据的可分页内存。

• 当未指定 place 时，Tensor 默认设备位置和安装的飞桨框架版本一致。如安装了 GPU 版本的飞桨，则设备位置默认为 GPU，即 Tensor 的place?默认为?paddle.CUDAPlace。

• 使用?paddle.device.set_device?可设置全局默认的设备位置。Tensor.place 的指定值优先级高于全局默认值。

#cpu
cpu_Tensor = paddle.to_tensor(1, place=paddle.CPUPlace())
print(cpu_Tensor.place)

#gpu
gpu_Tensor = paddle.to_tensor(1, place=paddle.CUDAPlace(0))
print(gpu_Tensor.place) # 显示Tensor位于GPU设备的第 0 张显卡上

#固定内存上
pin_memory_Tensor = paddle.to_tensor(1, place=paddle.CUDAPinnedPlace())
print(pin_memory_Tensor.place)

结果：

由于我没有安装GPU的paddle，所以只运行了CPU

名称

?Tensor 的名称是其唯一的标识符，为 Python 字符串类型

print("Tensor name:", paddle.to_tensor(1).name)

stop_gradient 属性

概念：

表示是否停止计算梯度，默认值为 True，表示停止计算梯度，梯度不再回传。

在设计网络时，如不需要对某些参数进行训练更新，可以将参数的stop_gradient设置为True。

代码：

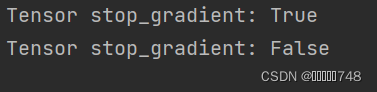
eg = paddle.to_tensor(1)
print("Tensor stop_gradient:", eg.stop_gradient)
eg.stop_gradient = False
print("Tensor stop_gradient:", eg.stop_gradient)

结果：

操作

索引和切片

概念：

通过索引或切片方式可访问或修改 Tensor。

特点：

1. 基于 0-n 的下标进行索引，如果下标为负数，则从尾部开始计算。

2. 通过冒号?:?分隔切片参数，start:stop:step?来进行切片操作，其中 start、stop、step 均可缺省。

访问Tensor：

• 针对一维 Tensor，仅有单个维度上的索引或切片：

ndim_1_Tensor = paddle.to_tensor([0, 1, 2, 3, 4, 5, 6, 7, 8])
print("Origin Tensor:", ndim_1_Tensor.numpy()) # 原始1维Tensor
print("First element:", ndim_1_Tensor[0].numpy()) # 取Tensor第一个元素的值？
print("Last element:", ndim_1_Tensor[-1].numpy())
print("All element:", ndim_1_Tensor[:].numpy())
print("Before 3:", ndim_1_Tensor[:3].numpy())
print("From 6 to the end:", ndim_1_Tensor[6:].numpy())
print("From 3 to 6:", ndim_1_Tensor[3:6].numpy())
print("Interval of 3:", ndim_1_Tensor[::3].numpy()) #取索引值，意思就是从开始到结束，每三个取一个值。
print("Reverse:", ndim_1_Tensor[::-1].numpy())  #表示将字符或数字倒序输出

结果：

?

?

• 针对二维及以上的?Tensor，则会有多个维度上的索引或切片：

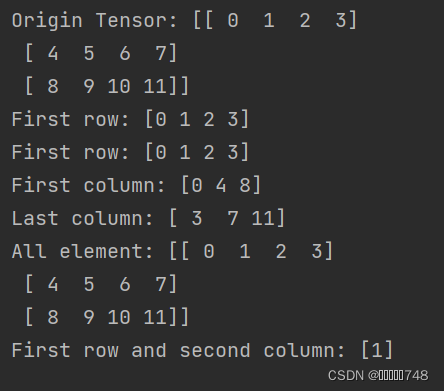
ndim_2_Tensor = paddle.to_tensor([[0, 1, 2, 3],
                                  [4, 5, 6, 7],
                                  [8, 9, 10, 11]])
print("Origin Tensor:", ndim_2_Tensor.numpy())
print("First row:", ndim_2_Tensor[0].numpy())
print("First row:", ndim_2_Tensor[0, :].numpy())
print("First column:", ndim_2_Tensor[:, 0].numpy())
print("Last column:", ndim_2_Tensor[:, -1].numpy())
print("All element:", ndim_2_Tensor[:].numpy())
print("First row and second column:", ndim_2_Tensor[0, 1].numpy())

结果：

?修改Tensor：

请慎重通过索引或切片修改 Tensor，该操作会原地修改该 Tensor 的数值，且原值不会被保存。如果被修改的 Tensor 参与梯度计算，仅会使用修改后的数值，这可能会给梯度计算引入风险。飞桨框架会自动检测不当的原位（inplace）使用并报错。

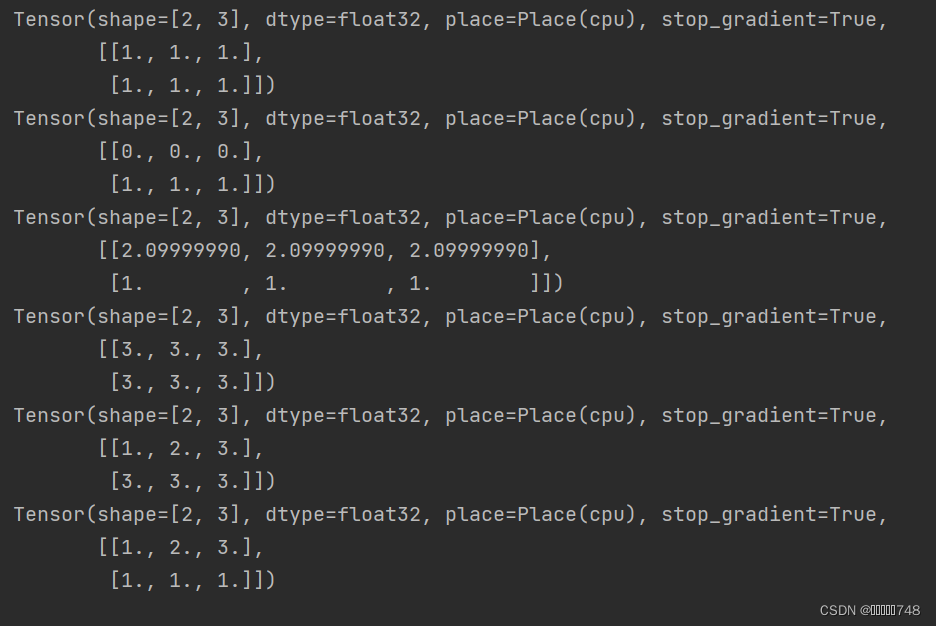
x = paddle.to_tensor(np.ones((2, 3)).astype(np.float32))
print(x)

x[0] = 0                     
print(x)

x[0:1] = 2.1  #第0维  
print(x)

x[...] = 3
print(x)

x[0:1] = np.array([1,2,3])
print(x)

x[1] = paddle.ones([3])
print(x)

?

结果：

API调用方法：

x = paddle.to_tensor([[1.1, 2.2], [3.3, 4.4]], dtype="float64")
y = paddle.to_tensor([[5.5, 6.6], [7.7, 8.8]], dtype="float64")

print(paddle.add(x, y), "\n") # 方法一
print(x.add(y), "\n") # 方法二

数学运算

x.abs()                       #逐元素取绝对值
x.ceil()                      #逐元素向上取整
x.floor()                     #逐元素向下取整
x.round()                     #逐元素四舍五入
x.exp()                       #逐元素计算自然常数为底的指数
x.log()                       #逐元素计算x的自然对数
x.reciprocal()                #逐元素求倒数
x.square()                    #逐元素计算平方
x.sqrt()                      #逐元素计算平方根
x.sin()                       #逐元素计算正弦
x.cos()                       #逐元素计算余弦
x.add(y)                      #逐元素相加
x.subtract(y)                 #逐元素相减
x.multiply(y)                 #逐元素相乘
x.divide(y)                   #逐元素相除
x.mod(y)                      #逐元素相除并取余
x.pow(y)                      #逐元素幂运算
x.max()                       #指定维度上元素最大值，默认为全部维度
x.min()                       #指定维度上元素最小值，默认为全部维度
x.prod()                      #指定维度上元素累乘，默认为全部维度
x.sum()                       #指定维度上元素的和，默认为全部维度

飞桨框架对 Python 数学运算相关的魔法函数进行了重写，举例：
x + y  -> x.add(y)            #逐元素相加
x - y  -> x.subtract(y)       #逐元素相减
x * y  -> x.multiply(y)       #逐元素相乘
x / y  -> x.divide(y)         #逐元素相除
x % y  -> x.mod(y)            #逐元素相除并取余
x ** y -> x.pow(y)            #逐元素幂运算

逻辑运算

x.isfinite()                  #判断Tensor中元素是否是有限的数字，即不包括inf与nan
x.equal_all(y)                #判断两个Tensor的全部元素是否相等，并返回形状为[1]的布尔类Tensor
x.equal(y)                    #判断两个Tensor的每个元素是否相等，并返回形状相同的布尔类Tensor
x.not_equal(y)                #判断两个Tensor的每个元素是否不相等
x.less_than(y)                #判断Tensor x的元素是否小于Tensor y的对应元素
x.less_equal(y)               #判断Tensor x的元素是否小于或等于Tensor y的对应元素
x.greater_than(y)             #判断Tensor x的元素是否大于Tensor y的对应元素
x.greater_equal(y)            #判断Tensor x的元素是否大于或等于Tensor y的对应元素
x.allclose(y)                 #判断Tensor x的全部元素是否与Tensor y的全部元素接近，并返回形状为[1]的布尔类Tensor


飞桨框架对 Python 逻辑比较相关的魔法函数进行了重写
x == y  -> x.equal(y)         #判断两个Tensor的每个元素是否相等
x != y  -> x.not_equal(y)     #判断两个Tensor的每个元素是否不相等
x < y   -> x.less_than(y)     #判断Tensor x的元素是否小于Tensor y的对应元素
x <= y  -> x.less_equal(y)    #判断Tensor x的元素是否小于或等于Tensor y的对应元素
x > y   -> x.greater_than(y)  #判断Tensor x的元素是否大于Tensor y的对应元素
x >= y  -> x.greater_equal(y) #判断Tensor x的元素是否大于或等于Tensor y的对应元素


以下操作仅针对 bool 型Tensor：
x.logical_and(y)              #对两个布尔类型Tensor逐元素进行逻辑与操作
x.logical_or(y)               #对两个布尔类型Tensor逐元素进行逻辑或操作
x.logical_xor(y)              #对两个布尔类型Tensor逐元素进行逻辑亦或操作
x.logical_not(y)              #对两个布尔类型Tensor逐元素进行逻辑非操作

线性代数

x.t()                         #矩阵转置
x.transpose([1, 0])           #交换第 0 维与第 1 维的顺序
x.norm('fro')                 #矩阵的弗罗贝尼乌斯范数
x.dist(y, p=2)                #矩阵（x-y）的2范数
x.matmul(y)                   #矩阵乘法

广播机制

在深度学习任务中，有时需要使用较小形状的 Tensor 与较大形状的 Tensor 执行计算，广播机制就是将较小形状的 Tensor 扩展到与较大形状的 Tensor 一样的形状，便于匹配计算，同时又没有对较小形状 Tensor 进行数据拷贝操作，从而提升算法实现的运算效率。?

广播条件

• 每个 Tensor 至少为一维 Tensor

• 从最后一个维度向前开始比较两个 Tensor 的形状，需要满足如下条件才能进行广播：两个 Tensor 的维度大小相等；或者其中一个 Tensor 的维度等于 1；或者其中一个 Tensor 的维度不存在。

# 可以广播的例子1
x = paddle.ones((2, 3, 4))
y = paddle.ones((2, 3, 4))
# 两个Tensor 形状一致，可以广播
z = x + y
print(z.shape)
# [2, 3, 4]

# 可以广播的例子2
x = paddle.ones((2, 3, 1, 5))
y = paddle.ones((3, 4, 1))
# 从最后一个维度向前依次比较：
# 第一次：y的维度大小是1
# 第二次：x的维度大小是1
# 第三次：x和y的维度大小相等
# 第四次：y的维度不存在
# 所以 x和y是可以广播的
z = x + y
print(z.shape)
# [2, 3, 4, 5]

# 不可广播的例子
x = paddle.ones((2, 3, 4))
y = paddle.ones((2, 3, 6))
# 此时x和y是不可广播的，因为第一次比较：4不等于6
# z = x + y
# ValueError: (InvalidArgument) Broadcast dimension mismatch.

结果：

?

计算规则

• 如果两个Tensor的形状的长度不一致，会在较小长度的形状矩阵前部添加1，直到两个Tensor的形状长度相等。

• 保证两个Tensor形状相等之后，每个维度上的结果维度就是当前维度上的较大值。

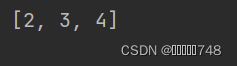
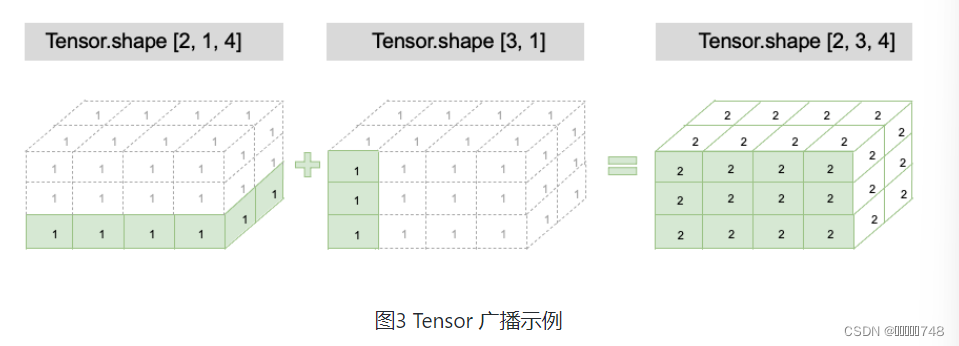
x = paddle.ones((2, 1, 4))
y = paddle.ones((3, 1)) # y的形状长度为2，小于x的形状长度3，因此会在y的形状前部添加1，结果就是y的形状变为[1, 3, 1]
z = x + y
print(z.shape)
# z的形状: [2,3,4]，z的每一维度上的尺寸，将取x和y对应维度上尺寸的较大值，如第0维x的尺寸为2，y的尺寸为1，则z的第0维尺寸为2

结果：

?

?

?

Tensor 与 Numpy 数组相互转换

异同

• Tensor 的很多基础操作 API 和 Numpy 在功能、用法上基本保持一致。如前文中介绍的指定数据、形状、区间创建 Tensor，Tensor 的形状、数据类型属性，Tensor 的各种操作，以及 Tensor 的广播，可以很方便地在 Numpy 中找到相似操作。

• 但是，Tensor 也有一些独有的属性和操作，而 Numpy 中没有对应概念或功能，这是为了更好地支持深度学习任务。如前文中介绍的通过图像、文本等原始数据手动或自动创建 Tensor 的功能，能够更便捷地处理数据，Tensor 的设备位置属性，可以很方便地将 Tensor 迁移到 GPU 或各种 AI 加速硬件上，Tensor 的 stop_gradient 属性，也是 Tensor 独有的，以便更好地支持深度学习任务。

• 基于 Numpy 数组创建 Tensor 时，飞桨是通过拷贝方式创建，与原始数据不共享内存。

numpy->tensor

tensor_temp = paddle.to_tensor(np.array([1.0, 2.0]))
print(tensor_temp)

tensor->numpy

tensor_to_convert = paddle.to_tensor([1.,2.])
tensor_to_convert.numpy()