[人工智能]机器学习模型4——聚类1（k-Means聚类）

1 前置知识

各种距离公式

2 主要内容

聚类是无监督学习，主要?于将相似的样本?动归到?个类别中。 在聚类算法中根据样本之间的相似性，将样本划分到不同的类别中，对于不同的相似度计算?法，会得到不同的聚类结果。
简单理解就是，有监督学习：回归和分类，有目标值；无监督学习：聚类和降维。

3 距离度量公式

3.1闵可夫斯基距离

公式：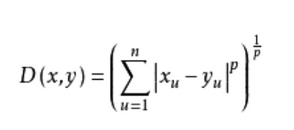

• 绝对距离
  当p=1时，得到绝对值距离，也叫曼哈顿距离（Manhattan distance）、出租汽车距离或街区距离（city block distance）。在二维空间中可以看出，这种距离是计算两点之间的直角边距离，相当于城市中出租汽车沿城市街道拐直角前进而不能走两点连接间的最短距离。绝对值距离的特点是各特征参数以等权参与进来，所以也称等混合距离。
• 欧氏距离
  当p=2时，得到欧几里德距离（Euclidean distance）距离，就是两点之间的直线距离（以下简称欧氏距离）。欧氏距离中各特征参数是等权的。
• 切比雪夫距离
  令p = 无穷，得到切比雪夫距离。

3.2 杰卡德相似度系数

定义：有两个集合A和B，那么这两个集合的杰卡德系数为A和B的交集除以A和B的并集。
用于比较两个样本之间的差异性和相似性。杰卡德系数越高，则两个样本相似度越高。
公式：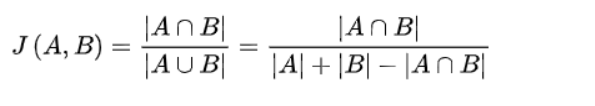
杰卡德距离是杰卡德系数的补集，用来描述两个集合的不相似度。
杰卡德距离：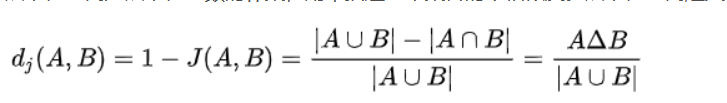

3.3 余弦相似度

定义：通过测量两个向量的夹角的余弦值来度量它们之间的相似性。
公式：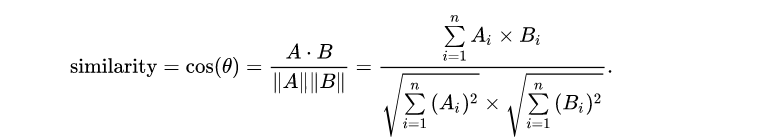

最常见的应用就是计算文本相似度。将两个文本根据他们词，建立两个向量，计算这两个向量的余弦值，就可以知道两个文本在统计学方法中他们的相似度情况。实践证明，这是一个非常有效的方法。

3.4 pearson相关系数

衡量两个连续变量之间的线性相关程度。
公式：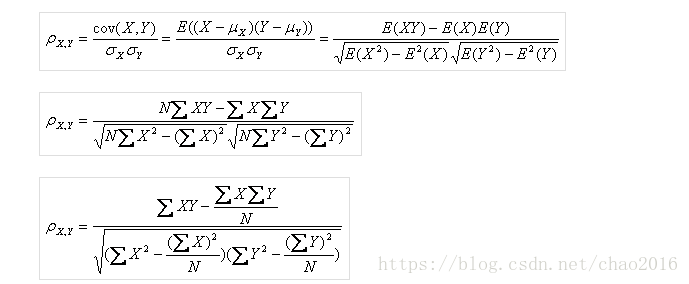

3.5 相对熵

又被称为Kullback-Leibler散度或信息散度，是两个概率分布（probability distribution）间差异的非对称性度量，即KL(p||q)不等于KL(q||p)。
设P(x)，Q(x)是随机变量X上的两个概率分布，则在离散和连续随机变量的情形下，相对熵的定义分别为：

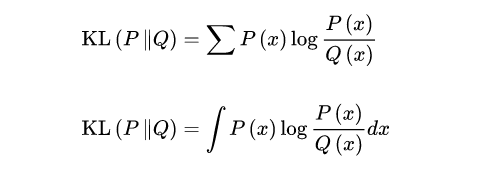
相对熵可以衡量两个随机分布之间的距离，当两个随机分布相同时，它们的相对熵为零，当两个随机分布的差别增大时，它们的相对熵也会增大。所以相对熵可以用于比较文本的相似度，先统计出词的频率，然后计算相对熵。另外，在多指标系统评估中，指标权重分配是一个重点和难点，也通过相对熵可以处理。

3.6 hellinger距离

海林格距离
可以看作相对熵的推广，当阿尔法趋近于1的时候
公式：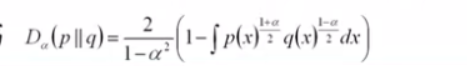

4 K-means算法

对初值敏感。
总结：
K-means聚类实现流程

• 事先确定常数K，常数K意味着最终的聚类类别数;
• 随机选定初始点为质?，并通过计算每?个样本与质?之间的相似度(这?为欧式距离)，将样本点归到最相似 的类中，
• 接着，重新计算每个类的质?(即为类中?)，重复这样的过程，直到质?不再改变，
• 最终就确定了每个样本所属的类别以及每个类的质?。
• 注意:由于每次都要计算所有的样本与每?个质?之间的相似度，故在?规模的数据集上，K-Means算法的收敛 速度?较慢。

4.1 K-Means 的API

 class sklearn.cluster.KMeans(n_clusters=8, *, init='k-means++', n_init=10, max_iter=300, tol=0.0001, verbose=0, random_state=None, copy_x=True, algorithm='lloyd')

参数：

• n_clusters: int，默认值=8
  要形成的簇数以及要生成的质心数。
• init: {‘k-means++’, ‘random’}, callable or array-like of shape (n_clusters, n_features), default=’k-means++’
  初始化方法：
  · “k-means++”：根据点对总惯量的贡献的经验概率分布，通过采样选择初始簇质心。这项技术加快了收敛速度。
  · “random”：从初始质心的数据中随机选择n个簇观测值（行）。
  如果数组被传递，它的形状应该是（n_clusters，n_features），并给出初始中心。
  如果传递了一个可调用函数，它应该接受参数X、n_clusters和一个随机状态，并返回一个初始化。
• n_init: int，default=10
  使用不同质心种子运行k-means算法的时间。最终结果将是n_init连续运行的最佳惯性输出。
• max_iter： int，default=300
  单个运行的k-means算法的最大迭代次数。
• tol：float，default=1e-4
  关于两个连续迭代的簇中心差的Frobenius范数的相对容差，以声明收敛。
• verbose：int, default=0
  冗余模式。
• random_state：int, RandomState instance or None, default=None
  确定质心初始化的随机数生成。使用int使随机性具有确定性。
• copy_x：bool，default=True
  在预计算距离时，先将数据居中会更精确。如果copy_x为True（默认值），则不会修改原始数据。如果为False，则会修改原始数据，并在函数返回之前放回，但通过减去然后再加上数据平均值可能会产生较小的数值差异。请注意，如果原始数据不是C连续的，即使copy_x为False，也会进行复制。如果原始数据是稀疏的，但不是CSR格式，则即使copy_x为False，也会制作副本。
• algorithm：{“lloyd”, “elkan”, “auto”, “full”}, default=”lloyd”
  K-means 要使用的算法。经典的EM型算法是“lloyd”。通过使用三角形不等式，“elkan”变量可以在某些具有明确簇的数据集上更有效。然而，由于分配了额外的形状数组（n_samples、n_clusters），它的内存消耗更大。不推荐使用“auto”和“full”，它们将在Scikit Learn 1.3中删除。它们都是“lloyd”的别名。

属性:

• cluster_centers_：ndarray of shape (n_clusters, n_features)
  集群中心的坐标。如果算法在完全收敛之前停止（参见tol和max_iter），则这些将与labels_不一致。
• labels_：ndarray of shape (n_samples,)
  每个点的标签
• inertia_：float
  样本到最近聚类中心的平方距离之和，如果提供了样本权重，则按样本权重加权。
• n_iter_：int
  运行的迭代次数。
• n_features_in_：int
  装配过程中看到的特征数量。
• feature_names_in_：ndarray of shape (n_features_in_,)
  配合期间看到的特征名称。仅当X具有全部为字符串的要素名称时才定义。

以下实际中对于k-means算法的优化。

4.2 canopy算法

4.3 K-means++

由于 K-means 算法的结果会受到初始点的选取而有所区别，因此有提出这种算法的改进: K-Means++ 。K-Means++算法选择初始聚类中心的基本原则是：初始的聚类中心之间的相互距离要尽可能的远。
kmeans++?的，让选择的质?尽可能的分散。
步骤

从数据集中随机选择一个点作为第一个聚类中心；

计算每个样本与当前已有聚类中心之间的最短距离D(x)，即与最近的一个聚类中心的距离。这个值越大，表示被选取作为聚类中心的概率较大；并计算每个样本被选为下一个聚类中心的概率 D ( x ) 2 ∑ x ? X D ( x ) 2 \frac{D(x)^2}{\sum_{x\epsilon X}{D(x)^2}} ∑x?X?D(x)2D(x)2?，最后用轮盘法选出下一个聚类中心。

重复过程（2）直到找到k个聚类中心。

选出初始点后，就继续使用标准的 K-Means算法 中第2步到第4步了。

缺点：由于聚类中心点选择过程中的内在有序性，在扩展方面存在着性能方面的问题(第k个聚类中心点的选择依赖前k-1个聚类中心点的值)。
sklearn的k-means算法默认选择的是k-means++进行初始化。

4.4 二分K-Means聚类

实现流程:

1. 所有点作为?个簇
2. 将该簇?分为?
3. 选择能最?限度降低聚类代价函数（也就是误差平?和）的簇划分为两个簇。
4. 以此进?下去，直到簇的数?等于?户给定的数?k为?。

 class sklearn.cluster.BisectingKMeans(n_clusters=8, *, init='random', n_init=1, random_state=None, max_iter=300, verbose=0, tol=0.0001, copy_x=True, algorithm='lloyd', bisecting_strategy='biggest_inertia')

• bisecting_strategy：{“biggest_inertia”, “largest_cluster”}, default=”biggest_inertia”
  定义应如何执行二等分：
  “biggest_initia”意味着BisectingKMeans将始终检查
  具有最大SSE（平方误差总和）的簇的所有计算簇并将其平分。这种方法注重精度，但在执行时间方面可能代价高昂（特别是对于较大数量的数据点）。
  “largest_cluster”-BisectingKMeans将始终使用
  之前计算的所有簇中分配给它的最大点数。这应该比由SSE（“biggest_inertia”）挑选更快，并且在大多数情况下可能会产生类似的结果。

4.5 k-medoids（k-中?聚类算法）

k-medoids算法能有效削弱异常点的影响。
K-medoids和K-means不?样的地?在于中?点的选取。

• K-means中，将中?点取为当前cluster中所有数据点的平均值，对异常点很敏感!
• K-medoids中，将从当前cluster 中选取到其他所有（当前cluster中的）点的距离之和最?的点作为中?点。
  算法流程：
  ( 1 )总体n个样本点中任意选取k个点作为medoids
  ( 2 )按照与medoids最近的原则，将剩余的n-k个点分配到当前最佳的medoids代表的类中
  ( 3 )对于第i个类中除对应medoids点外的所有其他点，按顺序计算当其为新的medoids时，代价函数的值，遍历所 有可能，选取代价函数最?时对应的点作为新的medoids
  ( 4 )重复2-3的过程，直到所有的medoids点不再发?变化或已达到设定的最?迭代次数
  ( 5 )产出最终确定的k个类
  k-medoids对噪声鲁棒性好。
  例：当?个cluster样本点只有少数?个，如（1,1）（1,2）（2,1）（1000,1000）。其中（1000,1000）是噪声。如果 按照k-means质??致会处在（1,1）（1000,1000）中间，这显然不是我们想要的。这时k-medoids就可以避免这种情 况，他会在（1,1）（1,2）（2,1）（1000,1000）中选出?个样本点使cluster的绝对误差最?，计算可知?定会在前三 个点中选取。
  k-medoids只能对?样本起作?，样本?，速度就太慢了，当样本多的时候，少数?个噪?对k-means的质?影响也没 有想象中的那么重，所以k-means的应?明显?k-medoids多。

4.6 Mini Batch K-Means

适合?数据的聚类算法
?数据量是什么量级？通常当样本量?于1万做聚类时，就需要考虑选?Mini Batch K-Means算法。
Mini Batch KMeans使?了Mini Batch（分批处理）的?法对数据点之间的距离进?计算。 Mini Batch计算过程中不必使?所有的数据样本，?是从不同类别的样本中抽取?部分样本来代表各?类型进?计算。 由于计算样本量少，所以会相应的减少运?时间，但另???抽样也必然会带来准确度的下降。
该算法的迭代步骤有两步：
(1)从数据集中随机抽取?些数据形成?批量，把他们分配给最近的质?
(2)更新质?
与Kmeans相?，数据的更新在每?个?的样本集上。对于每?个?批量，通过计算平均值得到更新质?，并把?批量 ?的数据分配给该质?，随着迭代次数的增加，这些质?的变化是逐渐减?的，直到质?稳定或者达到指定的迭代次数，停?计算。

class sklearn.cluster.MiniBatchKMeans(n_clusters=8, *, init='k-means++', max_iter=100, batch_size=1024, verbose=0, compute_labels=True, random_state=None, tol=0.0, max_no_improvement=10, init_size=None, n_init=3, reassignment_ratio=0.01)

• init_size: int, default=None
• 为了加速初始化而随机采样的样本数（有时以牺牲准确性为代价）：唯一的算法是通过对数据的随机子集运行批KMean来初始化的。这需要大于n_clusters。
  如果为“无”，如果为3batch_size<n_clusters，则启发式为init_size=3bach_size，否则为init_size = 3 * n_clusters。
• batch_size：int，default=1024
  小批量的大小。为了加快计算速度，可以将batch_size设置为大于256*个核心数，以在所有核心上启用并行性。
• reassignment_ratio: float, default=0.01
  控制要重新分配的中心的最大计数的分数。较高的值意味着低计数中心更容易重新分配，这意味着模型将需要更长的时间来收敛，但应该收敛到更好的聚类中。但是，值太高可能会导致收敛问题，特别是对于较小的批处理大小。

kernel kmeans 映射到?维空间

ISODATA 动态聚类，可以更改K值??

5 聚类的衡量指标

5.1 均一性、完整性、V-measure

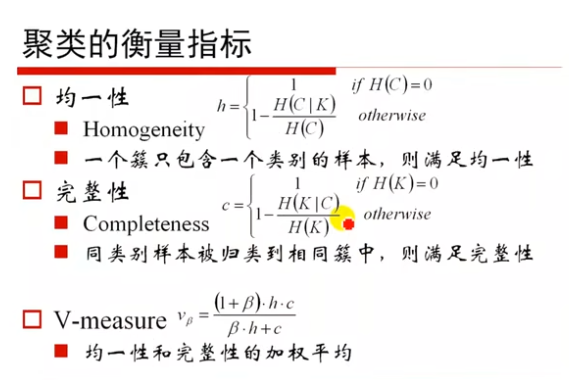
5.2 聚类效果评价指标: MI,NMI,AM(互信息，标准化互信息，调整互信息)

5.3 轮廓系数

5.4 CH系数（Calinski-Harabasz Index）

Calinski-Harabasz： 类别内部数据的协?差越?越好，类别之间的协?差越?越好（换句话说：类别内部数据的距离平?和越?越好，类别 之间的距离平?和越?越好）， 这样的Calinski-Harabasz分数s会?，分数s?则聚类效果越好。

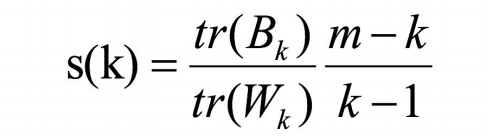
tr为矩阵的迹, Bk为类别之间的协?差矩阵，Wk为类别内部数据的协?差矩阵; m为训练集样本数，k为类别数。
CH需要达到的?的： ?尽量少的类别聚类尽量多的样本，同时获得较好的聚类效果。

5.5 外部指标：JC、FMI、RI

指的是：将聚类结果与某个参考模型作比较
外部指标主要包括三类：Jaccard 系数(简称JC)、FM 系数(简称FMI) 、Rand 指数(简称RI)。

5.5.1 JC

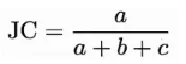
5.5.2Rand指数（Rand Index）

简称RI，也称兰德指数。

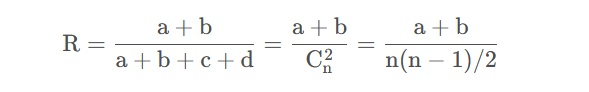
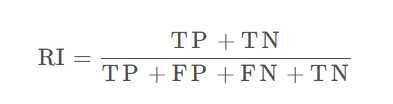
5.5.3 FMI指数

全称：Fowlkes and Mallows Index

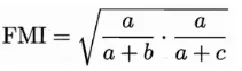
5.6 内部指标

直接对聚类结果进行分析

DBI

DI

聚类模型评估Clustering metrics API

sklearn.metrics.cluster子模块包含聚类分析结果的评估指标。

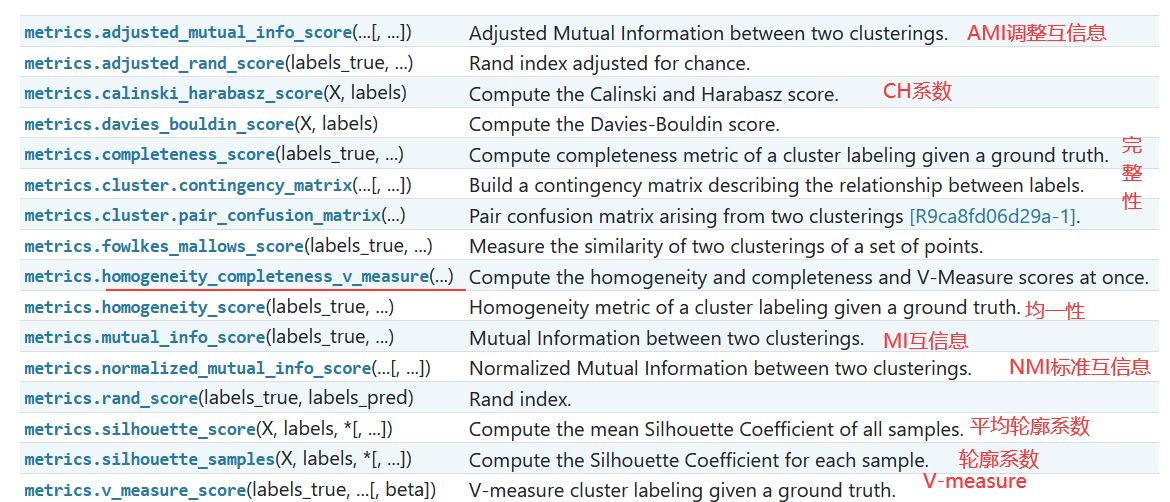
说明

因为聚类的内容比较多，聚类的层次聚类、密度聚类和谱聚类分别在 “机器学习模型4” 的聚类2，3，4节。
也在学习整理中，整理不全面，有需要再接着整理。

参考

1.聚类视频：https://www.bilibili.com/video/BV1Ca411M7KA/?p=9&spm_id_from=333.880.my_history.page.click&vd_source=c35b16b24807a6dbe33f5473659062ac
2.机器学习，周志华
3.黑马学习
4.https://blog.csdn.net/Amy9_Miss/article/details/104785606
5.密度聚类：https://blog.csdn.net/qq_38436431/article/details/120538371