[人工智能]【Machine Learning】9.逻辑回归产生的逻辑损失

1.导入

import numpy as np
%matplotlib widget
import matplotlib.pyplot as plt
from plt_logistic_loss import  plt_logistic_cost, plt_two_logistic_loss_curves, plt_simple_example
from plt_logistic_loss import soup_bowl, plt_logistic_squared_error
plt.style.use('./deeplearning.mplstyle')

2.逻辑回归的代价

squared error cost function 平方误差成本函数:
The equation for the squared error cost with one variable is 含一个变量的平方误差代价函数:
$$J(w,b)=\frac{1}{2m}\sum _{i=0}^{m?1}(f_{w,b}(x^{(i)})?y^{(i)}{)}^2\text{\hspace{1em}(1)}$$

where
$$f_{w,b}(x^{(i)})=w{x}^{(i)}+b\text{\hspace{1em}(2)}$$

x_train = np.array([0., 1, 2, 3, 4, 5],dtype=np.longdouble)
y_train = np.array([0,  0, 0, 1, 1, 1],dtype=np.longdouble)
plt_simple_example(x_train, y_train)

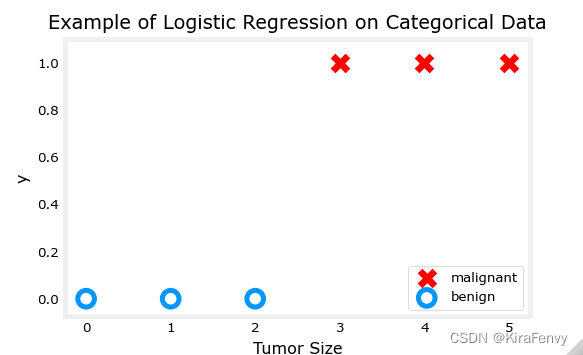
Now, let’s get a surface plot of the cost using a squared error cost:
$$J(w,b)=\frac{1}{2m}\sum _{i=0}^{m?1}(f_{w,b}(x^{(i)})?y^{(i)}{)}^2$$

where
$$f_{w,b}(x^{(i)})=sigmoid(w{x}^{(i)}+b)$$

plt.close('all')
plt_logistic_squared_error(x_train,y_train)
plt.show()

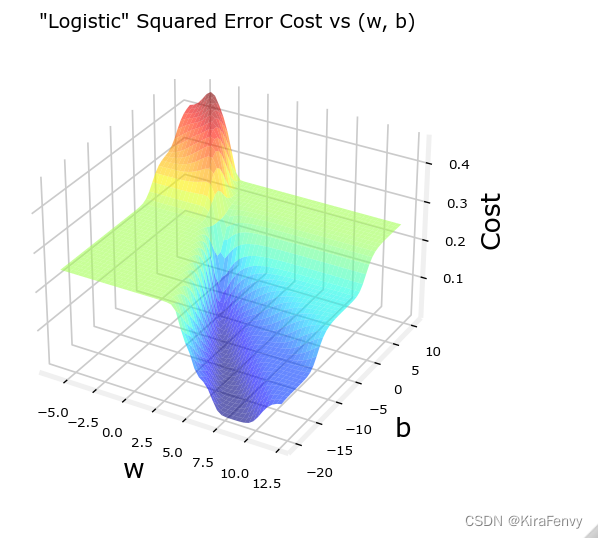
下面这是线性回归的

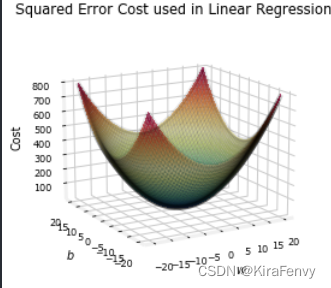
Logistic Regression使用的损失函数更适合目标为0或1而不是任何数字的分类任务。

Definition Note: In this course, these definitions are used:
Loss is a measure of the difference of a single example to its target value while the 损失是用来衡量单个数据与目标的差值
Cost is a measure of the losses over the training set 代价是用来衡量整个训练集上的损失

3.损失函数

损失是用来衡量单个数据与目标的差值，而代价是用来衡量整个训练集上的损失

This is defined:

• $loss(f_{\mathbf{w},b}({\mathbf{x}}^{(i)}),y^{(i)})$ is the cost for a single data point, which is:

• $f_{\mathbf{w},b}({\mathbf{x}}^{(i)})$ is the model’s prediction, while $y^{(i)}$ is the target value.

• $f_{\mathbf{w},b}({\mathbf{x}}^{(i)})=g(\mathbf{w}?{\mathbf{x}}^{(i)}+b)$ where function $g$ is the sigmoid function.

此损失函数的定义特征是它使用两条单独的曲线。一个用于目标为零（$y=0$）的情况，另一个用于当目标为一（$y=1$）时的情况。结合起来，这些曲线提供了对损失函数有用的表示，即，当预测与目标匹配时为零，当预测不同于目标时，值迅速增加。考虑以下曲线

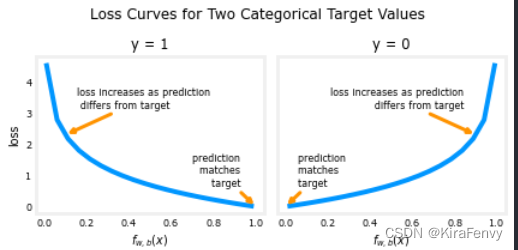
上面的损失函数可以写成更简单的形式
$$loss(f_{\mathbf{w},b}({\mathbf{x}}^{(i)}),y^{(i)})=(?y^{(i)}\log \left(f_{\mathbf{w},b}\left({\mathbf{x}}^{(i)}\right)\right)?\left(1?y^{(i)}\right)\log \left(1?f_{\mathbf{w},b}\left({\mathbf{x}}^{(i)}\right)\right)$$

上面那个式子看起来有点吓人，其实 $y^{(i)}$ 只有两个值 0 and 1.
当 $y^{(i)}=0$ 式子变成
$$\begin{array}{rl}loss(f_{\mathbf{w},b}({\mathbf{x}}^{(i)}),0)& =(?(0)\log \left(f_{\mathbf{w},b}\left({\mathbf{x}}^{(i)}\right)\right)?\left(1?0\right)\log \left(1?f_{\mathbf{w},b}\left({\mathbf{x}}^{(i)}\right)\right)\\ & =?\log \left(1?f_{\mathbf{w},b}\left({\mathbf{x}}^{(i)}\right)\right)\end{array}\text{\hspace{1em}?}$$
当 $y^{(i)}=1$ 式子变成
$$\begin{array}{rl}loss(f_{\mathbf{w},b}({\mathbf{x}}^{(i)}),1)& =(?(1)\log \left(f_{\mathbf{w},b}\left({\mathbf{x}}^{(i)}\right)\right)?\left(1?1\right)\log \left(1?f_{\mathbf{w},b}\left({\mathbf{x}}^{(i)}\right)\right)\\ & =?\log \left(f_{\mathbf{w},b}\left({\mathbf{x}}^{(i)}\right)\right)\end{array}\text{\hspace{1em}?}$$

这个损失函数，可以生成一个成本函数，它包含了所有示例中的损失，下面会讨论

plt.close('all')
cst = plt_logistic_cost(x_train,y_train)

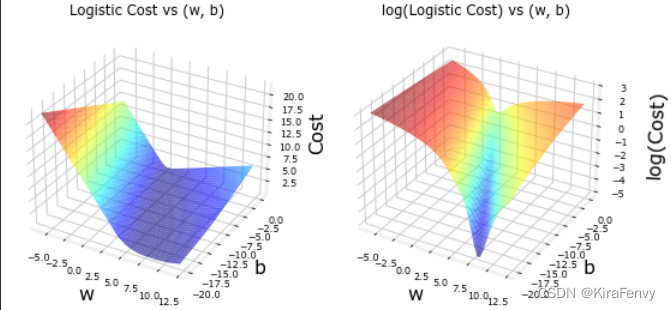
这条曲线非常适合梯度下降！它没有高原、局部极小值或间断（plateaus, local minima, or discontinuities）。注意，在平方误差的情况下，它不是一个碗。绘制成本和成本对数以说明这样一个事实，即当成本较小时，曲线有一个斜率，并继续下降。

4.从损失函数得出代价函数

4.1 导入

import numpy as np
%matplotlib widget
import matplotlib.pyplot as plt
from lab_utils_common import  plot_data, sigmoid, dlc
plt.style.use('./deeplearning.mplstyle')

4.2 数据载入与分析

X_train = np.array([[0.5, 1.5], [1,1], [1.5, 0.5], [3, 0.5], [2, 2], [1, 2.5]])  #(m,n)
y_train = np.array([0, 0, 0, 1, 1, 1])   

绘图

fig,ax = plt.subplots(1,1,figsize=(4,4))
plot_data(X_train, y_train, ax)

# Set both axes to be from 0-4
ax.axis([0, 4, 0, 3.5])
ax.set_ylabel('$x_1$', fontsize=12)
ax.set_xlabel('$x_0$', fontsize=12)
plt.show()

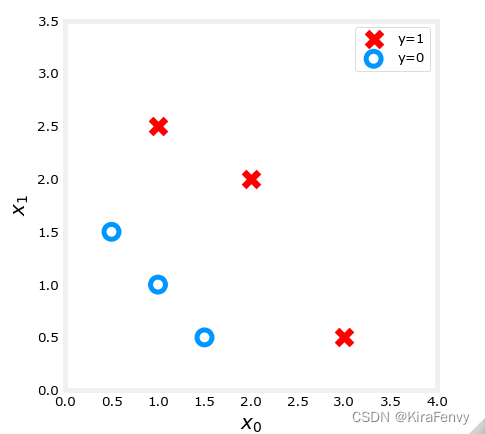
4.3 逻辑回归的代价计算

这里是把所有数据的loss合并为整个函数的cost

$$J(\mathbf{w},b)=\frac{1}{m}\sum _{i=0}^{m?1}\left[loss(f_{\mathbf{w},b}({\mathbf{x}}^{(i)}),y^{(i)})\right]\text{\hspace{1em}(1)}$$

where

• $loss(f_{\mathbf{w},b}({\mathbf{x}}^{(i)}),y^{(i)})$ is the cost for a single data point, which is:

  $$loss(f_{\mathbf{w},b}({\mathbf{x}}^{(i)}),y^{(i)})=?y^{(i)}\log \left(f_{\mathbf{w},b}\left({\mathbf{x}}^{(i)}\right)\right)?\left(1?y^{(i)}\right)\log \left(1?f_{\mathbf{w},b}\left({\mathbf{x}}^{(i)}\right)\right)\text{\hspace{1em}(2)}$$

• where m is the number of training examples in the data set and:
  $$\begin{array}{rl}{f}_{\mathbf{w},b}({\mathbf{x}}^{(\mathbf{i})})& =g(z^{(i)})\\ z^{(i)}& =\mathbf{w}?{\mathbf{x}}^{(i)}+b\\ g(z^{(i)})& =\frac{1}{1+e^{?z^{(i)}}}\end{array}\text{\hspace{1em}?}$$

计算代码：

def compute_cost_logistic(X, y, w, b):
    """
    Computes cost

    Args:
      X (ndarray (m,n)): Data, m examples with n features
      y (ndarray (m,)) : target values
      w (ndarray (n,)) : model parameters  
      b (scalar)       : model parameter
      
    Returns:
      cost (scalar): cost
    """

    m = X.shape[0]
    cost = 0.0
    for i in range(m):
        z_i = np.dot(X[i],w) + b
        f_wb_i = sigmoid(z_i)
        cost +=  -y[i]*np.log(f_wb_i) - (1-y[i])*np.log(1-f_wb_i)
             
    cost = cost / m
    return cost

调用上述代码

w_tmp = np.array([1,1])
b_tmp = -3
print(compute_cost_logistic(X_train, y_train, w_tmp, b_tmp))

4.4 举例计算

把上述代码应用在具体例子中

看看$w$的不同值输出的cost函数.

• In a previous lab, you plotted the decision boundary for $b=?3,w_0=1,w_1=1$. That is, you had w = np.array([-3,1,1]).

• Let’s say（假设） you want to see if $b=?4,w_0=1,w_1=1$, or w = np.array([-4,1,1]) provides a better model.

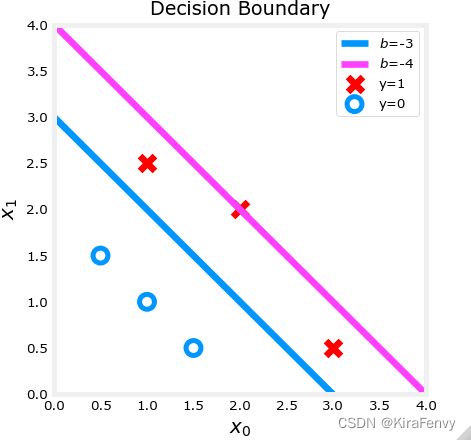
Let’s first plot the decision boundary for these two different $b$ values to see which one fits the data better.

• For $b=?3,w_0=1,w_1=1$, we’ll plot $?3+x_0+x_1=0$ (shown in blue)
• For $b=?4,w_0=1,w_1=1$, we’ll plot $?4+x_0+x_1=0$ (shown in magenta)

import matplotlib.pyplot as plt

# Choose values between 0 and 6
x0 = np.arange(0,6)

# Plot the two decision boundaries
x1 = 3 - x0
x1_other = 4 - x0

fig,ax = plt.subplots(1, 1, figsize=(4,4))
# Plot the decision boundary
ax.plot(x0,x1, c=dlc["dlblue"], label="$b$=-3")
ax.plot(x0,x1_other, c=dlc["dlmagenta"], label="$b$=-4")
ax.axis([0, 4, 0, 4])

# Plot the original data
plot_data(X_train,y_train,ax)
ax.axis([0, 4, 0, 4])
ax.set_ylabel('$x_1$', fontsize=12)
ax.set_xlabel('$x_0$', fontsize=12)
plt.legend(loc="upper right")
plt.title("Decision Boundary")
plt.show()

w_array1 = np.array([1,1])
b_1 = -3
w_array2 = np.array([1,1])
b_2 = -4

print("Cost for b = -3 : ", compute_cost_logistic(X_train, y_train, w_array1, b_1))
print("Cost for b = -4 : ", compute_cost_logistic(X_train, y_train, w_array2, b_2))


Cost for b = -3 :  0.36686678640551745
Cost for b = -4 :  0.5036808636748461

5.课后题