GAMMA归一化:
import cv2
import numpy as np
img = cv2.imread('gamma0.jpg',0)
img1 = np.power(img/float(np.max(img)), 1/1.5)
img2 = np.power(img/float(np.max(img)), 1.5)
# 这里就是gamma归一化操作 这里的gamma值分别是1/1.5 和 1.5
cv2.imshow('src',img)
cv2.imshow('gamma=1/1.5',img1)
cv2.imshow('gamma=1.5',img2)
cv2.waitKey(0)
# img = img * 255 # 校正后 ---> 量化到0~255为了减少光照因素的影响,降低图像局部的阴影和光照变化所造成的影响,我们首先采用Gamma校正法对输入图像的颜色空间进行标准化(或者说是归一化)。
所谓的Gamma校正可以理解为提高图像中偏暗或者偏亮部分的图像对比效果,能够有效地降低图像局部的阴影和光照变化。
##作者在他的博士论文里有提到,对于涉及大量的类内颜色变化,如猫,狗和马等动物,没标准化的RGB图效果更好,而牛,羊的图做gamma颜色校正后效果更好。 是否用gamma校正得分析具体的训练集情况。
像素梯度计算
举一个非常简单的例子
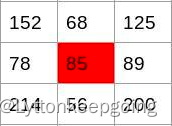
对于85这个像素点 他的梯度赋值为?
Gx?=∣89?78∣=11
Gy?=∣56?68∣=12
G=sqrt((Gx?)2+(Gy?)2)=13.6
梯度方向或者说是我们后面要用到的划分到bin中的角度为
theta=arctan(Gy?/Gx?)=36
HOG特征提取过程
把image划分为m个n*n的cells n就是我们的cell_size
然后统计每个cell里的梯度直方图 直方图划分为9个bin(论文中设置的最佳bin个数)
在0-180度范围内 一个bin代表20度 180度代表0(论文中提到使用180度无方向性的设置比360度好)
这里有个细节要注意,如果一个角度大于160度,也就是在160-180度之间,我们知道这里角度0,180度是一样的,所以在下面这个例子里,像素的角度为165度的时候,要把幅值按照比例放到0和160的bin里面去。如下图

?然后把所有cell的gradients的幅值都按direction分到这九个bin里可以得到一个梯度直方图

?然后对梯度直方图作归一化
将几个细胞单元(cell)组合成更大的块(block),这时整幅图像就可看成是待检测窗口,将更大的块看成是滑动窗口,依次从左到右从上到下进行滑动,得到一些有重复细胞单元的块及一些相同细胞单元(cell)在不同块(block)中的梯度信息,再对这些块(block)信息分别作归一化处理,不同的细胞单元尺寸大小及不同块的尺寸大小会影响最终的检测效果。然后block_vector就是我们抽取出来的hog_vector
具体代码为:
hog_vector = []
# 默认步长为一个cell大小,一个block由2x2个cell组成,遍历每一个block
for i in range(cell_gradient_vector.shape[0] - 1): # 16-1 = 15
for j in range(cell_gradient_vector.shape[1] - 1): # 8-1 = 15
# 每一个block由四个cell构成,因此,将相邻的四个cell的特征,存到一个列表中即可
block_vector = []
block_vector.extend(cell_gradient_vector[i][j])
block_vector.extend(cell_gradient_vector[i][j + 1])
block_vector.extend(cell_gradient_vector[i + 1][j])
block_vector.extend(cell_gradient_vector[i + 1][j + 1])
完整代码
#!/user/bin/env python3
# -*- coding: utf-8 -*-
# @Time : 2022-09-27 10:24
# @Author : Lyt
# @IDE : PyCharm
# @FileName : HOG.py
# @Blog : https://blog.csdn.net/m0_53292725?type=blog
"""
Histogram of Oriented Gradients
"""
# import cv2
# import numpy as np
#
#
# def is_inside(o, i): # o is inside i
# ox, oy, ow, oh = o
# ix, iy, iw, ih = i
# return ox < ix and oy < iy and ox+ow < ix+iw and oy+oh < iy+ih
#
#
# def draw_person(img, person):
# x, y, w, h = person
# cv2.rectangle(img, (x, y), (x+w, y+h), (0, 255, 255), 2) # img , min_xy, max_xy, rgb, thickness
#
#
# def detect():
# img = cv2.imread("/home/lyt/workspace/th.jpg")
# # print(img.shape)
# rows, cols = img.shape[:2]
# sacle = 1.0 # sacle_rate
# img = cv2.resize(img, dsize=(int(cols*sacle), int(rows*sacle)))
# # print(img.shape)
# """
# create HOG descriptor
# winSize = (64,128)
# blockSize = (16,16)
# blockStride = (8,8)
# cellSize = (8,8)
# nbins = 9
# hog = cv2.HOGDescriptor(winSize,blockSize,blockStride,cellSize,nbins)
#
# """
# hog = cv2.HOGDescriptor()
# detector = cv2.HOGDescriptor_getDefaultPeopleDetector()
# print("detector", type(detector), detector.shape)
# hog.setSVMDetector(detector) # set svm detector
#
#
# # multi-scale detection
# # found is a list of all the detected target box
#
# found, w = hog.detectMultiScale(img)
# print('found', type(found), found.shape)
# print(w)
# found_filtered = []
# for ri, r in enumerate(found):
# for qi, q in enumerate(found):
# if ri != qi and is_inside(r, q):
# break
# else:
# found_filtered.append(r)
#
# for person in found_filtered:
# draw_person(img, person)
#
# cv2.imshow(img)
# cv2.waitKey(0) # Waitkey controls the duration of the imshow
# cv2.destroyAllWindows()
#
#
#############################
import math
import cv2
import numpy as np
import matplotlib.pyplot as plt
class Hog_descriptor():
def __init__(self, img, cell_size=8, bin_size=9):
self.img = img
self.img = np.sqrt(img / float(np.max(img))) # sqrt so gamma=0.5
self.img = 255*self.img # back to 0-255
self.cell_size = cell_size
self.bin_size = bin_size
self.angle_unit = 180 / self.bin_size
def extract(self):
"""
计算图像的HOG描述符,以及HOG-image特征图
"""
height, width = self.img.shape
'''
1、计算图像每一个像素点的梯度幅值和角度
'''
# gradient_magnitude:shape为(128,64)
# 每个像素点的梯度值、梯度方向
gradient_magnitude, gradient_angle = self.global_gradient()
gradient_magnitude = abs(gradient_magnitude)
'''
2、计算输入图像的每个cell单元的梯度直方图,形成每个cell的descriptor 比如输入图像为128x64 可以得到16x8个cell,每个cell由9个bin组成
'''
# 梯度方向的特征向量初始化的shape为:(16,8,9)
cell_gradient_vector = np.zeros((int(height / self.cell_size), int(width / self.cell_size), self.bin_size))
# 遍历每一行、每一列
for i in range(cell_gradient_vector.shape[0]):
for j in range(cell_gradient_vector.shape[1]):
# 计算第[i][j]个cell的特征向量
cell_magnitude = gradient_magnitude[i * self.cell_size:(i + 1) * self.cell_size,
j * self.cell_size:(j + 1) * self.cell_size]
cell_angle = gradient_angle[i * self.cell_size:(i + 1) * self.cell_size,
j * self.cell_size:(j + 1) * self.cell_size]
cell_gradient_vector[i][j] = self.cell_gradient(cell_magnitude, cell_angle)
# 将得到的每个cell的梯度方向直方图绘出,得到特征图
hog_image = self.render_gradient(np.zeros([height, width]), cell_gradient_vector)
'''
3、将2x2个cell组成一个block,一个block内所有cell的特征串联起来得到该block的HOG特征descriptor
将图像image内所有block的HOG特征descriptor串联起来得到该image(检测目标)的HOG特征descriptor,
这就是最终分类的特征向量
'''
hog_vector = []
# 默认步长为一个cell大小,一个block由2x2个cell组成,遍历每一个block
for i in range(cell_gradient_vector.shape[0] - 1): # 16-1 = 15
for j in range(cell_gradient_vector.shape[1] - 1): # 8-1 = 15
# 每一个block由四个cell构成,因此,将相邻的四个cell的特征,存到一个列表中即可
block_vector = []
block_vector.extend(cell_gradient_vector[i][j])
block_vector.extend(cell_gradient_vector[i][j + 1])
block_vector.extend(cell_gradient_vector[i + 1][j])
block_vector.extend(cell_gradient_vector[i + 1][j + 1])
'''块内归一化梯度直方图,去除光照、阴影等变化,增加鲁棒性'''
# 计算l2范数
# 计算的目标是一个矩阵,4*9的矩阵
# 将矩阵中的每一个元素按照L2范数进行归一化 。因此先求矩阵的平方和,再把元素除以平方和
# 下面lambda函数的作用就是求和, 得到一个数字
mag = lambda vector: math.sqrt(sum(i ** 2 for i in vector))
magnitude = mag(block_vector) + 1e-5
# 归一化
if magnitude != 0:
# 第二行别看错了,normalize就是一个匿名函数而已, 跟 p没什么区别
normalize = lambda block_vector, magnitude: [element / magnitude for element in block_vector]
block_vector = normalize(block_vector, magnitude)
hog_vector.append(block_vector)
return np.asarray(hog_vector), hog_image
def global_gradient(self):
"""
分别计算图像沿x轴和y轴的梯度
"""
gradient_values_x = cv2.Sobel(self.img, cv2.CV_64F, 1, 0, ksize=5)
gradient_values_y = cv2.Sobel(self.img, cv2.CV_64F, 0, 1, ksize=5)
# 计算梯度幅值 这个计算的是0.5*gradient_values_x + 0.5*gradient_values_y
# gradient_magnitude = cv2.addWeighted(gradient_values_x, 0.5, gradient_values_y, 0.5, 0)
# 计算梯度方向
# gradient_angle = cv2.phase(gradient_values_x, gradient_values_y, angleInDegrees=True)
gradient_magnitude, gradient_angle = cv2.cartToPolar(gradient_values_x, gradient_values_y,
angleInDegrees=True)
# 角度大于180°的,减去180度
gradient_angle[gradient_angle > 180.0] -= 180
# print('gradient',gradient_magnitude.shape,gradient_angle.shape,np.min(gradient_angle),np.max(gradient_angle))
return gradient_magnitude, gradient_angle
def cell_gradient(self, cell_magnitude, cell_angle):
"""
为每个细胞单元构建梯度方向直方图
args:
cell_magnitude:cell中每个像素点的梯度幅值,
cell_angle:cell中每个像素点的梯度方向
return:
返回该cell对应的梯度直方图,长度为bin_size
"""
# 构建每一个cell的梯度直方图,因为分箱分成了9个,初始化时,orientation_centers=[0,0,0,0,0,0,0,0,0]
orientation_centers = [0] * self.bin_size
# 遍历cell中的每一个像素点
for i in range(cell_magnitude.shape[0]):
for j in range(cell_magnitude.shape[1]):
# 梯度幅值
gradient_strength = cell_magnitude[i][j]
# 梯度方向
gradient_angle = cell_angle[i][j]
# 参考双线性插值的方式赋予权重
# min_angle: 第i个索引, max_angle : 第i+1个索引, 这里的命名真是有问题
# 下标的范围是0到8
min_angle, max_angle, weight = self.get_closest_bins(gradient_angle)
orientation_centers[min_angle] += (gradient_strength * (1 - weight))
orientation_centers[max_angle] += (gradient_strength * weight)
return orientation_centers
def get_closest_bins(self, gradient_angle):
"""
计算梯度方向gradient_angle位于哪一个bin中,这里采用的计算方式为双线性插值
具体参考:https://www.leiphone.com/news/201708/ZKsGd2JRKr766wEd.html
例如:当我们把180°划分为9个bin的时候,分别对应对应0,20,40,...160这些角度。
角度是10,副值是4,因为角度10介于0-20度的中间(正好一半),所以把幅值
一分为二地放到0和20两个bin里面去。
args:
gradient_angle:角度
return:
start,end,weight:起始bin索引,终止bin的索引,end索引对应bin所占权重
"""
idx = int(gradient_angle / self.angle_unit) # 如int(165/20) = 8
mod = gradient_angle % self.angle_unit # 165%20 = 15。 u= 15/20 = 0.75, 则分到idx的梯度的值的权重为1-u = 0.25
return idx % self.bin_size, (idx + 1) % self.bin_size, mod / self.angle_unit # 分到idx+1的权重为u = 0.75
# 之所以要对9取余,防止越界。因为9*20=180。180度在分箱的时候实际上属于0度
def render_gradient(self, image, cell_gradient):
"""
将得到的每个cell的梯度方向直方图绘出,得到特征图
args:
image:画布,和输入图像一样大 [h,w]
cell_gradient:输入图像的每个cell单元的梯度直方图,形状为[h/cell_size,w/cell_size,bin_size]
return:
image:特征图
"""
cell_width = self.cell_size / 2
max_mag = np.array(cell_gradient).max() # 获取(累计)梯度最大值,用于归一化;在可视化画图时,采取的是整个图片的最大值归一化
# 遍历每一个cell
for x in range(cell_gradient.shape[0]): # cell_gradient:(16,8,9),当然,只是一个例子
for y in range(cell_gradient.shape[1]):
# 获取第[i][j]个cell的梯度直方图
cell_grad = cell_gradient[x][y] # cell_grad是一个9维的向量
# 归一化
cell_grad /= max_mag
angle = 0
angle_gap = self.angle_unit # 范围为20度
# 遍历每一个bin区间
for magnitude in cell_grad:
# 转换为弧度
angle_radian = math.radians(angle)
# 计算起始坐标和终点坐标,长度为幅值(归一化),幅值越大、绘制的线条越长、越亮
# 只是使用如下的方式,来可视化每个点的幅值大小
x1 = int(x * self.cell_size + cell_width + magnitude * cell_width * math.cos(angle_radian))
y1 = int(y * self.cell_size + cell_width + magnitude * cell_width * math.sin(angle_radian))
x2 = int(x * self.cell_size + cell_width - magnitude * cell_width * math.cos(angle_radian))
y2 = int(y * self.cell_size + cell_width - magnitude * cell_width * math.sin(angle_radian))
cv2.line(image, (y1, x1), (y2, x2), int(255 * math.sqrt(magnitude)))
angle += angle_gap
return image
if __name__ == '__main__':
# 加载图像
img_copy = cv2.imread('/home/user/lyt/th.jpg')
img_rgb = cv2.cvtColor(img_copy, cv2.COLOR_BGR2RGB)
width = 64
height = 128
# img_copy = img[320:320 + height, 570:570 + width][:, :, ::-1]
# gray_copy = cv2.cvtColor(img_copy, cv2.COLOR_BGR2GRAY)
gray_copy = cv2.cvtColor(img_copy, cv2.COLOR_BGR2GRAY)
# 显示原图像
plt.figure(figsize=(6.4, 2.0 * 3.2))
plt.subplot(1, 2, 1)
plt.imshow(img_rgb)
# HOG特征提取
hog = Hog_descriptor(gray_copy, cell_size=8, bin_size=9)
hog_vector, hog_image = hog.extract()
print('hog_vector', hog_vector.shape)
print('hog_image', hog_image.shape)
# 绘制特征图
plt.subplot(1, 2, 2)
plt.imshow(hog_image, cmap=plt.cm.gray)
plt.show()
TODO:svm,双线性插值, normalize