[人工智能]【PaperReading】DAEGC : Attributed Graph Clustering: A Deep Attentional Embedding Approach

DAEGC: 属性图聚类 : 一种深度注意力嵌入方法

论文作者：Chun Wang, Shirui Pan, Ruiqi Hu, Guodong Long, Jing Jiang, Chengqi Zhang
论文来源：2019, IJCAI
论文地址：https://arxiv.org/pdf/1906.06532.pdf
论文代码：https://github.com/Tiger101010/DAEGC

摘要

Graph clustering is a fundamental task which discovers communities or groups in networks. Recent studies have mostly focused on developing deep learning approaches to learn a compact graph embedding, upon which classic clustering methods like k-means or spectral clustering algorithms are applied.
图聚类是一项基本任务，可以在网络中发现社区或群体。最近的研究主要集中在开发深度学习方法上，以学习紧凑的图嵌入（a compact graph embedding），采用经典的聚类方法（例如K-均值或谱聚类算法）。

These two-step frameworks are difficult to manipulate and usually lead to suboptimal performance, mainly because the graph embedding is not goal-directed, i.e., designed for the specific clustering task.
这些two-step框架很难操纵，并且通常会导致次优性能，这主要是因为图嵌入不是目标导向的，即为特定的聚类任务而设计。

In this paper, we propose a goal-directed deep learning approach, Deep Attentional Embedded Graph Clustering (DAEGC for short). Our method focuses on attributed graphs to sufficiently explore the two sides of information in graphs.
在本文中，我们提出了一种目标导向的深度学习方法，深度注意力嵌入图聚类（简称DAEGC）。我们的方法着重于属性图，以充分探索图信息的两个方面。

By employing an attention network to capture the importance of the neighboring nodes to a target node, our DAEGC algorithm encodes the topological structure and node content in a graph to a compact representation, on which an inner product decoder is trained to reconstruct the graph structure.
通过使用注意力网络来捕获相邻节点对目标节点的重要性，我们的DAEGC算法编码图中的拓扑结构和节点内容以获得一种紧凑的表征，在此基础上，训练一个内积解码器来重建图结构。

Furthermore, soft labels from the graph embedding itself are generated to supervise a self-training graph clustering process, which iteratively refines the clustering results. The self-training process is jointly learned and optimized with the graph embedding in a unified framework, to mutually benefit both components.
此外，从图嵌入本身生成软标签（soft labels）来监督自训练图聚类过程，从而迭代地细化聚类结果。通过将图嵌入到统一的框架中，联合学习和优化自训练过程，使两个组件都受益。

Experimental results compared with state-of-the-art algorithms demonstrate the superiority of our method.
实验结果与最好的算法进行了比较，证明了该方法的优越性。

1. Introduction

Graph clustering aims to partition the nodes in the graph into disjoint groups。Further for attributed graph clustering, a key problem is how to capture the structural relationship and exploit the node content information.
图聚类的目的是将图中的节点划分为互不相交的组。典型的应用包括社区检测、群体细分、企业社交网络中的功能群体发现。此外，对于属性图聚类，关键问题是如何捕获结果关系并利用节点内容信息。

The drawback of two-step approaches is that the learned embedding may not be the best fit for the subsequent graph clustering task, and the graph clustering task is not beneficial to the graph embedding learning.
为解决这一问题，现有研究采用了深度学习技术来学习紧凑表示，以挖掘内容和结构数据的丰富信息。然而所有这些基于图嵌入的方法都是两步方法。为了实现两个步骤的互相促进，目标导向的训练框架是非常可取的。传统的目标导向训练模型大多应用于分类任务。现有的关于图聚类的目标定向嵌入方法的研究较少。

we propose a goal directed graph attentional autoencoder based attributed graph clustering framework in this paper.
在此基础上，本文提出了一种基于属性图聚类的目标定向图注意自动编码器。为了利用各种类型图数据的相互关系，本文提出以图注意力自编码器来学习潜在表示。

• 编码器使用一个图注意力网络来同时利用图结构信息和节点内容，并且多层编码器被堆叠在一起，以构建用于embedding学习的深度架构。
• 另一边的解码器则对拓扑图信息进行重构，并对潜在图表示进行操作。
• 进一步采用了一个自训练模块，它对“confident“的集群分配软标签来指导优化过程。

本文的主要贡献总结如下：

1. 开发了一种基于图注意力的自动编码器，以有效地整合结构和内容信息，用于深度潜在表征学习
2. 提出了一种目标导向带属性图聚类框架。该框架将嵌入学习和图聚类进行了联合优化，实现了两个组件的双赢
3. 实验结果表明，该算法的性能优于最新的图形聚类方法。

本文模型与传统的two-step方法的比较如Figure 1所示：

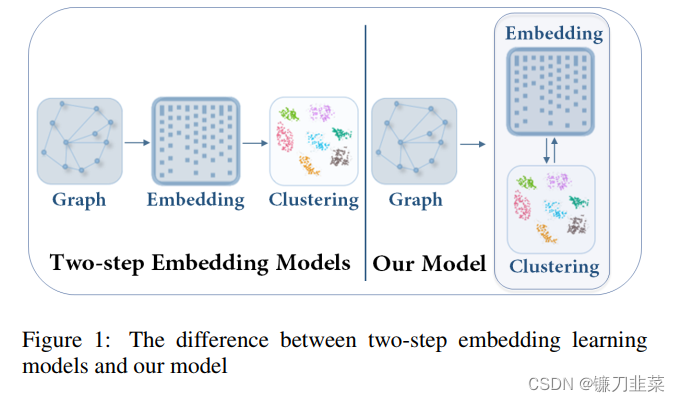
• 本文模型是将节点表示和聚类放在一个统一的框架中学习。
• Two-step方法则是先学习node embedding，然后进行聚类。

所谓目标导向，就是说特征提取和聚类任务不是独立的，提取的特征要在一定程度上有利于聚类，那么如何实现？可以通过自训练聚类的方式，将隐藏图嵌入产生的软聚类分配与聚类联合优化。

2. Related Work

1. 图聚类

• Earlty methods: Many embedding learning based approaches apply an existing clustering algorithm on the learned embedding
• In recent years, Many deep graph clustering algorithms employ autoencoders

2. 深度聚类算法

• Deep Embedded Clustering (DEC) is a specialized clustering technique. This method employs a stacked denoising autoencoder learning approach.
• After obtaining the hidden representation of the autoencoder by pre-train, the encoder pathway is fine-tuned by a defined Kullback-Leibler divergence clustering loss.

3. Problem Definition and Overall Framework

这里考虑属性图中的聚类任务。令$G=(V,E,X)$表示图，其中 V = { v i } i = 1 , . . . , n V=\{v_i\}_{i=1,...,n} V={vi?}i=1,...,n?表示节点集， E = { e i , j } E=\{e_{i,j}\} E={ei,j?}是节点之间的边的集合。图$G$的拓扑结构用邻接矩阵$A$表示，其中$A_{i,j}=1$如果$(v_i,v_j)\in E$；否则$A_{i,j}=0$。$X=x_1;...;x_n$是属性值，其中$x_i\in R^m$是与顶点$v_i$相连的实数属性向量（real-value attribute vector）。

给定一个图$G$，图聚类的目标是将$G$中的节点划分到$k$个不相交的组 { G 1 , G 2 , . . . , G k } \{G_1,G_2,...,G_k\} {G1?,G2?,...,Gk?}，因此使得同一簇内的节点通常：
(1) 在图结构方面彼此接近，而在其他方面相距较远；
(2) 更有可能具有相似的属性值。

总体框架如图2所示，包含两个部分：a graph attentional autoencoder和a self-training clustering module。

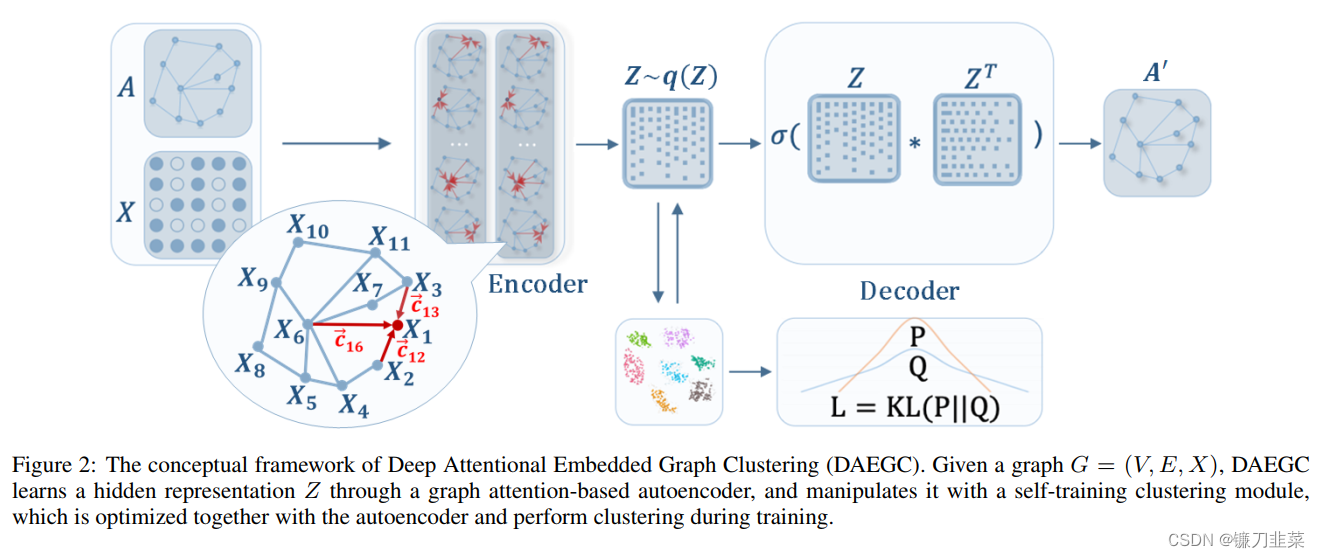
• Graph Attentional Autoencoder： 自动编码器以属性和图结构作为输入，通过最小化重构损失来学习潜在嵌入
• Self-training Clustering: 自训练模块根据学习到的表示进行聚类，同时根据当前聚类结果操作潜在表示。

4. Proposed Method

作者将这种方法称为Deep Attentional Embedded Graph Clustering (DAEGC)，首先开发一种图注意力自动编码器，它可以有效地整合图结构和内容信息，以学习潜在表示。 基于该表示，提出了一种自训练模块，以指导聚类算法取得更好的性能。

1. 图注意力自编码器

Graph attentional encoder(GAT encoder)：

为了同时表示图结构$A$和节点内容$X$，本文提出了一个图注意网络的变体作为图编码器。其思想是通过关注其邻居来学习每个节点的隐藏表示，并在隐藏表示中将属性值与图结构相结合。最直接的策略是将它的表示与它的所有邻居整合起来。为了度量不同邻居的重要性，在分层图注意策略中，对邻居表示给出了不同的权重。即采用图注意力机制，衡量node $i$的邻居$N_i$对于节点$i$的影响：
$$z_i^{l+1}=\sigma (\sum _{j\in N_i}{\alpha }_{ij}W{z}_j^l)(1)$$
其中，$z_i^{l+1}$表示节点$i$的输出表征，$N_i$表示$i$的邻居，${\alpha }_{ij}$是注意力系数，表示邻居节点$j$对节点$i$的重要性。$\sigma$是一个非线性函数。

为了计算${\alpha }_{ij}$，我们从属性值（attribute values）和拓扑距离（topological distance）两个方面度量了节点$j$的重要性。

• Aspect 1: attribute values
  注意力系数${\alpha }_{ij}$可以表示为 由 $x_i$ 和 $x_j$ 拼接形成的单层前馈神经网络：
  $$c_{i,j}=a^T[W{x}_i||W{x}_j](2)$$
  其中$a^T\in R^{2m^{\prime }}$是权重向量。

• Aspect 2: topological distance
  我们提出在编码器中利用high-order neighbors。通过考虑图中的t阶邻居节点信息（ t-order neighbor nodes），得到proximity matrix` :
  $$M=(B+B^2+...+B^t)/t,(3)$$
  其中$B$是转移矩阵（transition matrix），如果$e_{ij}\in E$有边相连，那么$B_{ij}=1/d_i$，否则$B_{ij}=0$。$d_i$是节点$i$的度。因此$M_{ij}$表示节点$j$到节点$i$的 t 阶内的拓扑相关性。如果节点 i 和 节点j存在邻居关系（t 阶之内），那么 $M_{ij}>0$。其中$t$可以针对不同的数据集灵活选择，以平衡模型的精度和效率。

注意力系数通常使用softmax函数对所有邻居$j\in {\mathbf{N}}_i$进行归一化，使其在节点间易于比较：
$${\alpha }_{i,j}=softma{x}_j(c_{ij})=\frac{exp(c_{ij})}{{\sum }_{r\in N_i}exp(c_{ir})}(4)$$
增加拓扑权重$M$和一个激活函数$\delta$(这里使用LeakyReLU)，注意力系数公式可以被写为：
$${\alpha }_{i,j}=\frac{exp(\delta M_{ij}(a^T[W{x}_i||W{x}_j]))}{{\sum }_{r\in N_i}exp(\delta M_{ir}(a^T[W{x}_i||W{x}_r]))}(5)$$
本文有$x_i=z_i^0$作为问题的输入，将两个图注意层堆叠起来：
$$z_i^{(1)}=\sigma (\sum _{j\in N_i}{\alpha }_{ij}{W}^{(0)}{x}_j),(6)$$
$$z_i^{(2)}=\sigma (\sum _{j\in N_i}{\alpha }_{ij}{W}^{(1)}{z}_j^{(1)}),(7)$$

通过上述图注意力编码器，得到最终的$z_i=z_i^{(2)}$。

Inner product decoder

现在有各种各样的解码器，它们重构图的结构、属性值或两者都重构。由于之前的潜在嵌入（latent embedding）已经包含了内容和结构的信息，所以本文选择了一种简单的内积解码器来预测节点之间的链接：
$${\hat{A}}_{ij}=sigmoid(z_i^T,z_j),(8)$$
其中$\hat{A}$是图的重构结构矩阵。

Reconstruction loss

通过度量$A$和$\hat{A}$之间差异来最小化重构误差：
$$L_r=\sum _{i=1}^{n}loss(A_{i,j},{\hat{A}}_{i,j}),(9)$$

2. Self-optimizing Embedding

图聚类任务是无监督的，在训练过程中无法反馈学到的嵌入是否得到了很好的优化。为了应对这一挑战，开发了一种自优化的嵌入算法作为解决方案。
除了优化重构误差之外，本文还将我们的hidden embedding放到自优化聚类模块中，使以下目标最优化：
$$L_c=KL(P||Q)=\sum _i\sum _u{p}_{iu}log\frac{p_{iu}}{q_{iu}},(10)$$
其中$q_{iu}$度量了节点嵌入$z_i$和聚类中心嵌入${\mu }_u$之间的相似度。通过 Student’s t-distribution 对其度量，使得它可以处理不同规模的集群并且计算方便：
$$q_{iu}=\frac{(1+||z_i?{\mu }_u|{|}^2{)}^{?1}}{{\sum }_k(1+||z_i?{\mu }_k|{|}^2{)}^{?1}},(11)$$
可以看作是每个节点的软聚类分配分布(soft clustering assignment distributions)。

另一方面，$p_{iu}$是目标分布，定义为:
$$p_{iu}=\frac{q_{iu}^2/{\sum }_i{q}_{iu}}{{\sum }_k(q_{ik}^2/{\sum }_i{q}_{ik})}(12)$$

在$Q$中，高概率值的软分配（soft assignments）被认为是值得信任的（trustworthy）。因此，目标分配$P$将$Q$提高2次方，以强调那些“confident assignments”的作用。聚类损失迫使当前分布$Q$接近目标分布$P$，从而将这些“confident assignments”设置为软标签来监督$Q$的embedding learning。

为此，首先训练不带自优化聚类部分的自编码器，以获得获得像公式(7)所述的有意义的embedding $z$。然后执行自优化聚类来改进这种embedding。通过公式(11)得到的所有节点$Q$的软聚类分配分布，在训练整个模型之前，对embedding $z$进行一次k-means聚类，得到初始的聚类中心$\mu$。

在接下来的训练中，使用基于$L_c$相对于 𝛍 和 𝒛 的梯度的 随机梯度下降(SGD) 更新聚类中心 𝛍 和embedding 𝒛 。

根据公式(12)计算目标分布𝑷 ，根据公式(10)计算聚类损失$L_c$。

目标分布$P$在训练过程中作为“ground-truth label”，但也依赖于当前的软分配Font metrics not found for font: .，每次迭代都会更新。在每一次迭代中更新𝑷是危险的，𝙌作为目标的不断变化会阻碍学习和收敛。为了避免自优化过程中的不稳定性，本文在实验中每5次更新𝑷。

综上所述，本文将聚类损失最小化，帮助自动编码器利用嵌入自身的特性来操纵嵌入空间，分散嵌入点，从而获得更好的聚类性能。

3. Joint Embedding and Clustering Optimization

本文联合优化了自动编码器embedding和聚类学习，并将最终优化函数定义为：
$$L=L_r+\gamma L_c,(13)$$
其中，$L_r$和$L_c$分别是重构损失和聚类损失。$\gamma \ge 0$为控制两者平衡的系数。可以从最后优化的𝙌中直接得到聚类结果，对于节点$v_i$的估计标签可以得到：
$$s_i=argma{x}_u{q}_{iu},(14)$$
这就是最后一个软分配分布𝙌中最有可能的分配。算法1中对上述流程进行总结：

DAEGC算法有以下优点：

• 相互剥削（Interplay Exploitation）。基于图注意网络的自动编码器有效地利用了结构信息和内容信息之间的相互作用。
• 聚类专门化Embedding（Clustering Specialized Embedding）。提出的自训练聚类组件对嵌入进行操作，提高了聚类性能。
• 共同学习（Joint Learning）。该框架在统一框架下联合优化了loss函数的两部分，学习嵌入和聚类。

5. Experiments

1. Benchmark Datasets

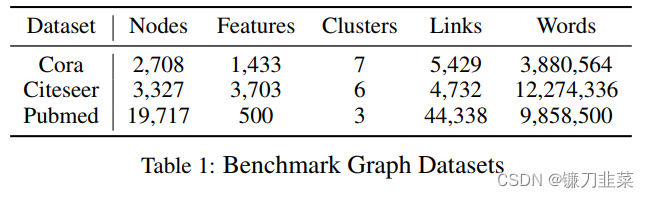
2. Baseline Methods

图聚类算法包括仅使用节点属性或网络结构信息的方法，以及结合两者的方法。 还比较了基于深度表示学习的图聚类算法.
Methods Using Structure or Content Only

• K-means
• Spectral clustering
• GraphEncoder: trains a stacked sparse autoencoder to obtain representation
• DeepWalk: is a structure-only representation learning method.
• DNGR: uses stacked denoising autoencoders and encodes each vertex into a low dimensional vector representation.
• M-NMF: is a Nonnegative Matrix Factorization model targeted at community-preserved embedding.
  Methods Using Both Structure and Content
• RMSC: robust multi-view spectral clustering method. We regard structure and content data as two views of information.
• TADW: regards DeepWalk as a matrix factorization method and adds the features of vertices for representation learning.
• VGAE & GAE: combine graph convolutional network with the (variational) autoencoder to learn representations
• DAEGC: is our proposed unsupervised deep attentional embedded graph clustering.

3. Evaluation Metrics & Parameter Settings

Metrics:

• Accuracy (ACC)
• Normalized Mutual Information (NMI)
• F-score
• Adjusted Rand Index (ARI)

一个好的聚类结果通常上面的指标具有较高的值。
Baseline Settings：
For the baseline algorithms, we carefully select the parameters for each algorithm, following the procedures in the original papers.

In TADW, for instance, we set the dimension of the factorized matrix to 80 and the regularization parameter to 0.2;
For the RMSC algorithm, we regard graph structure and node content as two different views of the data and construct a Gaussian kernel on them.

We run the k-means algorithm 50 times to get an average score for all embedding learning methods for fair comparison.

Parameter Settings：
For our method, we set the clustering coefficient $\gamma$ to 10. We consider second-order neighbors and set $M=(B+B^2)=2$. The encoder is constructed with a 256-neuron hidden layer and a 16-neuron embedding layer for all datasets.

4. 实验结果

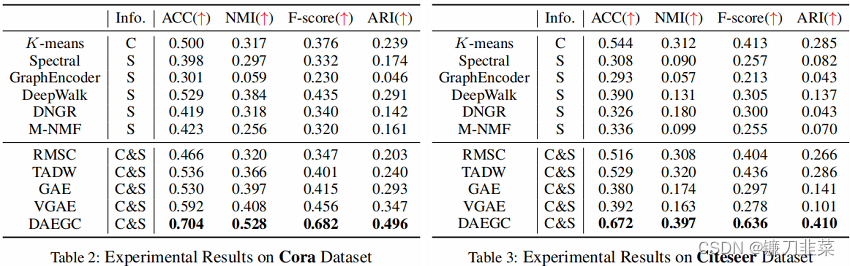
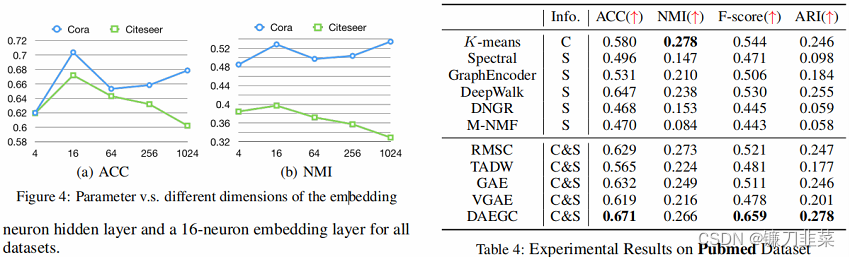
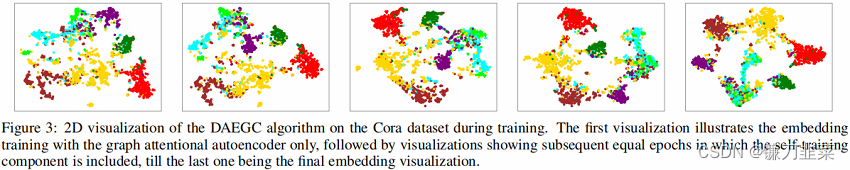
6. Conclusion

In this paper, we propose an unsupervised deep attentional embedding algorithm, DAEGC, to jointly perform graph clustering and learn graph embedding in a unified framework.
在本文中，我们提出了一种无监督的深度注意力嵌入算法：DAEGC，将执行图聚类和学习图嵌入两个过程整合到一个同意的框架下。

The learned graph embedding integrates both the structure and content information and is specialized for clustering tasks.
学习得到的图嵌入同时整合了结构信息和内容信息，并且是专门针对聚类任务的。

While the graph clustering task is naturally unsupervised, we propose a self-training clustering component that generates soft labels from “confident” assignments to supervise the embedding updating.
尽管图聚类任务天然是无监督的，但是我们提出了一个自训练聚类组件，用来从“confident”分配中生成soft labels，去监督embedding更新过程。

The clustering loss and autoencoder reconstruction loss are jointly optimized to simultaneously obtain both graph embedding and graph clustering result.
将聚类损失和编码器重构损失结合起来同时优化，不仅可以获得图embedding，还可以获得图聚类结果。

A comparison of the experimental results with various state-of-the-art algorithms validate DAEGC’s graph clustering performance.
和多种最好的算法比较，以及实验分析证明了DAEGC的图聚类性能。

总结

此文是发表在2019年IJCAI上关于图聚类问题的一篇文章。它提出了一种深度注意力嵌入的图聚类方法（ Deep Attentional Embedded Graph Clustering），主要解决传统的网络嵌入方法不能很好地应用于特定任务场景下的问题。

按照作者的思路，在经历第一波图注意力编码器的特征提取之后，所得到的结点的特征表示被直接用于聚类，并根据聚类的结果，生成对应的$P/Q$分布。那么实际上作者就默认了初始化的聚类结果是可以信赖的，即经过编码器的特征提取得到的聚类结果能够总体上呈现图的聚类情况，后续的训练则会进行一些调整，但总体的框架已经定下。

那么回到作者所提出的问题，大部分嵌入方法实际上是没有任务导向的，那么作者依然通过这种无任务导向的结点特征生成了可以信赖的初始化聚类。即从某种程度上而言，作者并没有解决文章开头所提到的问题。

参考资料

[1] https://arxiv.org/pdf/1906.06532.pdf
[2] https://www.cnblogs.com/BlairGrowing/p/15908418.html
[3] https://blog.csdn.net/qq_44015059/article/details/106586777
[4] https://blog.csdn.net/qq_32119213/article/details/106498344
[5] https://zhuanlan.zhihu.com/p/353693848