[人工智能]目标检测中对与Retinanet和Focal Loss的解析

Retinanet

2017年前，最先进的的对象检测器基于two-stage，proposal-driven的机制（典型如R-CNN），第一阶段生成大量候选框，第二阶段使用CNN将每个候选框分为目标类别或北京。论文Focal Loss for Dense Object Detection提出了one-stage的检测器，使得one-stage网络首次与two-stage网络相匹配甚至超越。

为了实现此目标，论文将训练时类别不均衡视作主要问题，并针对此问题提出了focal loss。

To achieve this result, we identify class imbalance during training as the main obstacle impeding one-stage detector from achieving state-of-the-art accuracy and propose a new loss function that eliminates this barrier.

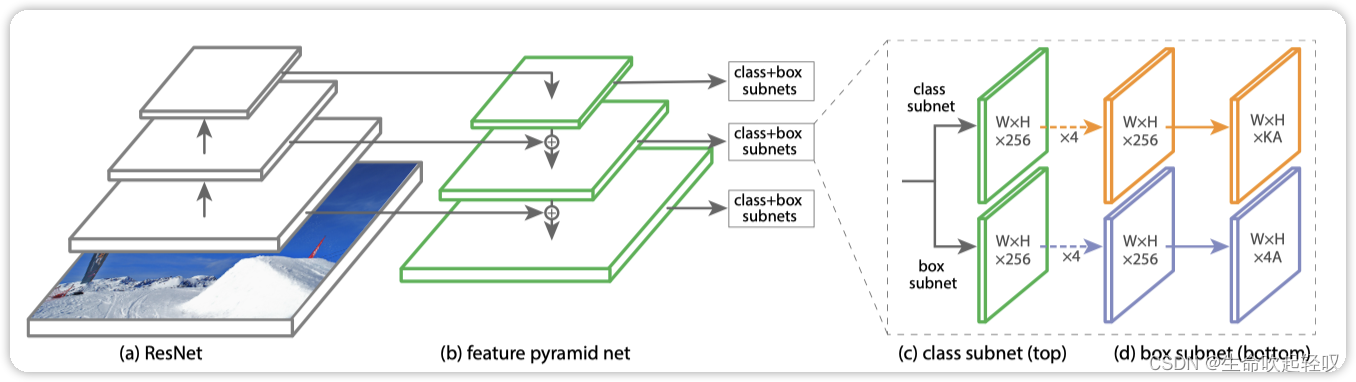
Rerinanet是一个单一的统一 网络，由一个backbone网络和两个特定任务的子网络组成。backbone负责计算输入图像的卷积特征图，其中一个子网负责对backbone的输出执行卷积对象分类，另一个子网负责执行卷积边界框回归。

The backbone is responsible for computing a convolutional feature map over an entire input image and is an off-the-self convolutional network. The ?rst subnet performs convolutional object classi?cation on the backbone’s output; the second subnet performs convolutional bounding box regression.

backbone

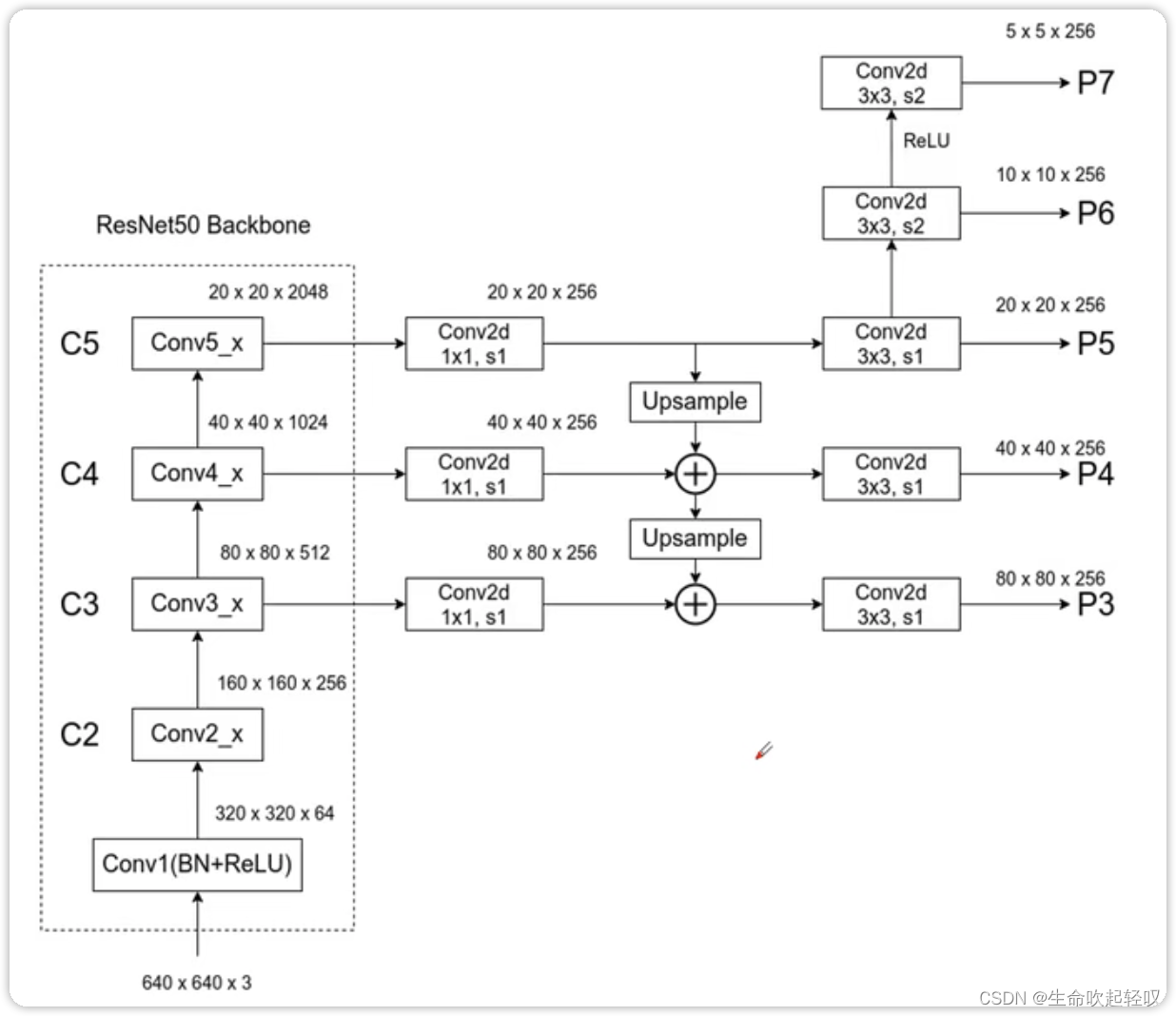
上图为Retinanet的backbone结构，同样采用了FPN的结构，金字塔的每一层都可以检测不同比例的物体。其中的不同与传统FPN的点在于原FPN中会使用C2来生成P2，而在Retinanet中并没有这样做，其给出的理由是P2会占用更多的计算资源；在原FPN中，P6是经过了一个最大池化下采样层进行下采样的，而这里则通过卷积层得到；同时，在Retinanet中，多出的P7经过一个ReLU激活函数，在经过一个卷积层后得到的。

anchors

在Rerinanet中，作者使用平移不变的anchor，并针对每一个特征层，使用了三个scale和三个ratio，也就是九组anchor。

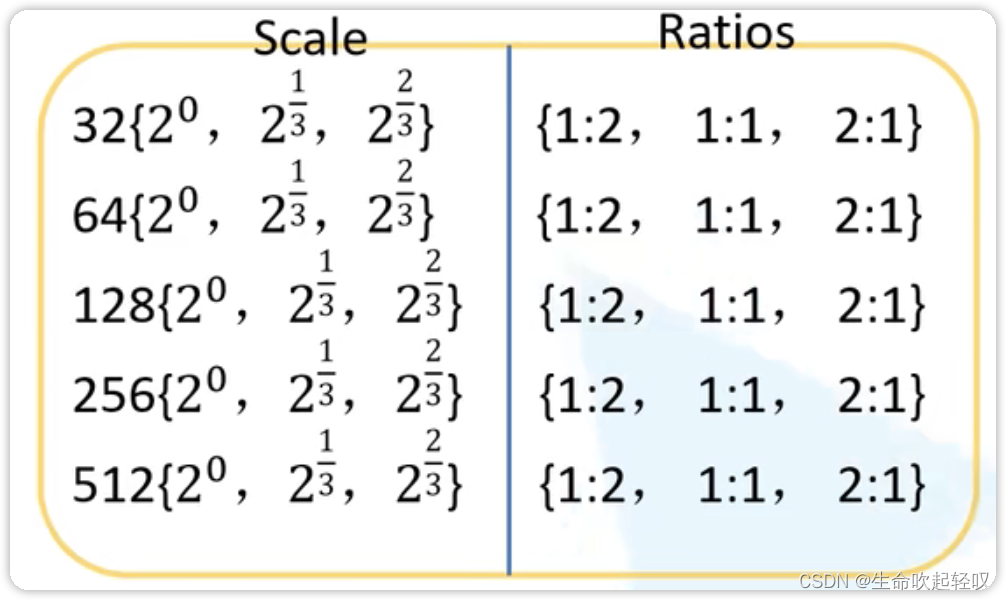
对于P3，第一类anchor使用$32^2?2^0$的面积，第二类anchor使用$32^2?2^{\frac{1}{3}}$的面积，第三类anchor使用$32^2?2^{\frac{2}{3}}$的面积，对于每一类anchor，使用1:2，1:1，2:1的ratio，于是对于每一个特征层，就有9个anchor。P4,P5,P6,P7同理。这好比把一张图像使用不同大小的网格进行划分，然后在不同大小的网格中预测目标。这些anchor覆盖了图中32-812的像素。

subnet

Retinanet的子网其实和Faster RCNN的类似，分别是目标分类和目标边界框框回归参数。
对于class subnet，使用四个33大小的卷积层，并在后面紧跟一个ReLU激活，最后是具有KA滤波器的33卷积层，K为监测目标类别数（不包括背景），A为anchor个数，等于9。
对于box subnet，它俩共用一个公共结构，但使用不同的参数，最后是C=4A的卷积层。（传统faster RCNN是4KA即每一个anchor对于每种类别都生成一组边界框回归参数，但这里使用类别不可知的预测方式）

Focal Loss

Focal Loss用于解决one-stage目标检测阶段场景中，在训练时前景和背景类别之间存在极端不平衡的问题。简单来说，这和我们生成的众多候选框有关，one-stage目标检测算法常常将输入图片划分成不同大小的网格（如上所说），而每个网格又包含了若干个候选框，因此生成了非常多的候选框，但可能只有少数几个候选框是真实包含目标的，这几个真实包含目标的候选框就是正样本，其他的为负样本，这导致了训练时正负样本极度不平衡。

Focal Loss提出了一种利用权重的方法来控制正负样本，分为两种方式：

• 控制正负样本的权重
• 控制容易分类和难分类样本的权重

控制正负样本的权重

常用交叉熵为
$$CE(p,y)=?(y?log(p)+(1?y)?log(1?p))$$
也可以写成
$$CE(p,y)=CE(p_t)=?log(p_t)$$
其中
$$p_t=\{\begin{array}{ll}p& ify=1\\ 1?p& otherwise\end{array}$$
在此不再赘述。想要降低负样本的影响，可以在常规的损失函数前增加一个系数α∈ [0, 1]，与$p_t$类似，当label=1时，${\alpha }_t=\alpha$，当lable=otherwise时，${\alpha }_t=1?\alpha$，此时我们便可以通过设置α实现控制正负样本对loss的贡献
$$CE(p_t)=?{\alpha }_{t}log(p_t)$$
其中
$${\alpha }_t=\{\begin{array}{ll}\alpha & ify=1\\ 1?\alpha & otherwise\end{array}$$
分解开则为
$$CE(p,y,\alpha )=\{\begin{array}{ll}?log(p)?\alpha & ify=1\\ ?log(1?p)?(1?\alpha )& ify=0\end{array}$$
由此我们可以知道，当α为0-0.5之间时，意味着我们可以降低正样本的loss权重而增加负样本的权重，反过来同理。因此通过改变α的值我们就可以改变正负样本的权重了。

控制容易分类和难分类样本的权重

对于一个样本，其是某个类的概率$p_t$越大，其越容易分类，所以利用$1?p_t$就可以计算出其属于容易分类或那分类，容易分类权重小，难分类权重大。
$$FL(p_t)=?(1?p_t{)}^{\gamma }log(p_t)$$
其中$(1?p_t{)}^{\gamma }$为调制系数。
当$p_t$趋于0时，调制系数趋于1，对总的loss贡献大，反之贡献小

两种权重控制方法合并

当两种方法合并，就是论文所提出的Focal Loss：
$$FL(p_t)=?{\alpha }_t(q?p_t{)}^{\gamma }log(p_t)$$