文章目录
摘要
本周学习了Transformer模型,以及Encoder和Decoder原理讲解与其Pytorch逐行实现,主要从6个细节难点去学习了Transformer的原理与实现,详细地学习了Transformer的word embedding、position embedding和mask原理。
一、Transformer
文献参考:https://arxiv.org/abs/1706.03762
文献题目:Attention Is All You Need
1.1 为什么要使用attention
1)因为t时刻的计算依赖于t-1时刻的计算结果,这样会导致模型的并行能力受到限制。
2)虽然在之前学习到的LSTM可以在一定程度上缓解长期依赖的问题,但是对于特别长期的依赖问题,LSTM是无法解决问题的,也就是说在encoder和decoder之间的语义向量无法保存过多的信息。
1.2 Transformer的优点
它采用了Attention机制,将序列中的任意两个位置之间的距离是缩小为一个常量,并且它不类似于RNN的顺序结构,因此具有较好的并行性,也符合现有的GPU框架。
在论文中,Transformer没有使用到传统的CNN和RNN,整个网络由Attention机制组成。
二、Transformer模型Encoder和Decoder原理讲解与其Pytorch逐行实现
如下图所示,这6个方面是Transformer学习的难点。
2.1 word embedding
关于word embedding,以序列建模为例,考虑source sentence 和 target sentence。
构建序列,序列的字符以其在词表中的索引的形式表示。
src_seq:输入的句子,第一个长度为2,第二个长度为4。
tgt_seq:目标的句子,第一个长度为4,第二个长度为3。
import numpy as np
import torch
import numpy
import torch.nn as nn
import torch.nn.functional as F
batch_size = 2
# 单词表大小
max_num_src_words = 8
max_num_tgt_words = 8
# 序列的最大长度
max_src_seq_len = 5
max_tgt_seq_len = 5
model_dim = 8
max_position_len = 5
src_len = torch.Tensor([2, 4]).to(torch.int32)
tgt_len = torch.Tensor([4, 3]).to(torch.int32)
print(src_len)
print(tgt_len)
2.2 单词索引构成源句子和目标句子
Step 1:用随机数生成句子单词索引,对句子做了padding,也就是对空白位置补0,以保证所有句子的长度一致,最后用torch,cat将两个句子张量拼接在一起。
src_seq = torch.cat([torch.unsqueeze(F.pad(torch.randint(1, max_num_src_words, (L,)), (0, max_src_seq_len - L)), 0)
for L in src_len])
tgt_seq = torch.cat([torch.unsqueeze(F.pad(torch.randint(1, max_num_tgt_words, (L,)), (0, max_tgt_seq_len - L)), 0)
for L in tgt_len])
print(src_seq)
print(tgt_seq)
输出源句子和目标句子
tensor([[6, 7, 0, 0, 0],
[7, 1, 5, 7, 0]])
tensor([[1, 5, 6, 2, 0],
[4, 7, 5, 0, 0]])
构造embedding
Step 2:构建word embedding,我们需要得到向量化的句子,也就是先构建词表embedding,再利用索引得到向量化的句子。
src_embedding_table = nn.Embedding(max_num_src_words + 1, model_dim)
tgt_embedding_table = nn.Embedding(max_num_tgt_words + 1, model_dim)
src_embedding = src_embedding_table(src_seq)
tgt_embedding = tgt_embedding_table(tgt_seq)
print(src_embedding)
print(tgt_embedding)
输出src_embedding和tgt_embedding
tensor([[[ 4.0562e-01, -4.7774e-01, 1.1197e+00, 2.5271e-01, -2.8610e-01,
-1.7786e+00, -3.4801e-01, 5.9147e-02],
[ 4.0562e-01, -4.7774e-01, 1.1197e+00, 2.5271e-01, -2.8610e-01,
-1.7786e+00, -3.4801e-01, 5.9147e-02],
[-1.1680e-01, 2.6256e-01, 9.0318e-01, 2.5852e-01, -6.7806e-01,
-3.2029e-01, 5.9314e-01, 1.4338e-01],
[-1.1680e-01, 2.6256e-01, 9.0318e-01, 2.5852e-01, -6.7806e-01,
-3.2029e-01, 5.9314e-01, 1.4338e-01],
[-1.1680e-01, 2.6256e-01, 9.0318e-01, 2.5852e-01, -6.7806e-01,
-3.2029e-01, 5.9314e-01, 1.4338e-01]],
[[ 2.0992e+00, 4.3112e-01, 1.1805e-03, 1.9759e-01, -7.2922e-01,
-2.1830e+00, -1.0120e-02, -4.0442e-01],
[ 1.7823e-01, -4.7776e-01, -1.1815e+00, -1.3451e+00, -1.1886e+00,
1.7289e+00, -3.9730e-01, 6.2238e-01],
[-1.0617e+00, -2.1093e-01, -1.1825e+00, -6.9534e-01, -4.2309e-01,
3.7529e-01, -1.8998e-01, 1.1653e-02],
[-1.0617e+00, -2.1093e-01, -1.1825e+00, -6.9534e-01, -4.2309e-01,
3.7529e-01, -1.8998e-01, 1.1653e-02],
[-1.1680e-01, 2.6256e-01, 9.0318e-01, 2.5852e-01, -6.7806e-01,
-3.2029e-01, 5.9314e-01, 1.4338e-01]]],
grad_fn=<EmbeddingBackward0>)
tensor([[[-0.6926, 0.3298, 0.8671, -3.5071, 1.3463, -0.5505, -0.5561,
-0.7192],
[-1.7076, -0.5672, -0.1689, 0.8521, 1.2127, 0.6972, 0.6094,
0.5606],
[-0.6211, -0.0036, 1.6586, -0.0787, 0.2682, -1.5178, -1.5031,
-1.7362],
[-1.3177, 1.1583, 0.4895, 0.9380, 0.8419, -0.0501, -1.0925,
-0.7124],
[ 1.5036, -0.3206, -0.2090, -0.2941, -0.0675, -0.1443, -0.5557,
0.5938]],
[[-1.7076, -0.5672, -0.1689, 0.8521, 1.2127, 0.6972, 0.6094,
0.5606],
[-0.5977, -0.7804, -1.0782, 1.7742, 2.0498, 0.4659, -1.1477,
1.5279],
[-0.6211, -0.0036, 1.6586, -0.0787, 0.2682, -1.5178, -1.5031,
-1.7362],
[ 1.5036, -0.3206, -0.2090, -0.2941, -0.0675, -0.1443, -0.5557,
0.5938],
[ 1.5036, -0.3206, -0.2090, -0.2941, -0.0675, -0.1443, -0.5557,
0.5938]]], grad_fn=<EmbeddingBackward0>)
2.3 构建position embedding
如下图所示,我们根据论文中的公式去构建position embedding。
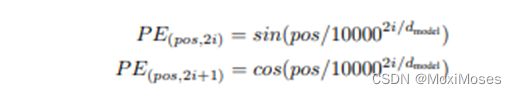
Step 3:pe_embedding_table[:, 0::2]得到偶数列编码,pe_embedding_table[:, 1::2]得到奇数列编码。
构建位置索引,再通过nn.embedding就可以直接得到position embedding。
pos_mat = torch.arange(max_position_len).reshape((-1, 1))
i_mat = torch.pow(10000, torch.arange(0, 8, 2).reshape(1, -1) / model_dim)
pe_embedding_table = torch.zeros(max_position_len, model_dim)
# 偶数列
pe_embedding_table[:, 0::2] = torch.sin(pos_mat / i_mat)
# 奇数列
pe_embedding_table[:, 1::2] = torch.cos(pos_mat / i_mat)
# print(pos_mat)
# print(i_mat)
# print(pe_embedding_table)
pe_embedding = nn.Embedding(max_position_len, model_dim)
pe_embedding.weight = nn.Parameter(pe_embedding_table, requires_grad=False)
src_pos = torch.cat([torch.unsqueeze(torch.arange(max(src_len)), 0) for _ in src_len]).to(torch.int32)
tgt_pos = torch.cat([torch.unsqueeze(torch.arange(max(tgt_len)), 0) for _ in tgt_len]).to(torch.int32)
src_pe_embedding = pe_embedding(src_pos)
tgt_pe_embedding = pe_embedding(tgt_pos)
print(src_pe_embedding)
print(tgt_pe_embedding)
输出src_pe_embedding和tgt_pe_embedding
tensor([[[ 0.0000e+00, 1.0000e+00, 0.0000e+00, 1.0000e+00, 0.0000e+00,
1.0000e+00, 0.0000e+00, 1.0000e+00],
[ 8.4147e-01, 5.4030e-01, 9.9833e-02, 9.9500e-01, 9.9998e-03,
9.9995e-01, 1.0000e-03, 1.0000e+00],
[ 9.0930e-01, -4.1615e-01, 1.9867e-01, 9.8007e-01, 1.9999e-02,
9.9980e-01, 2.0000e-03, 1.0000e+00],
[ 1.4112e-01, -9.8999e-01, 2.9552e-01, 9.5534e-01, 2.9995e-02,
9.9955e-01, 3.0000e-03, 1.0000e+00]],
[[ 0.0000e+00, 1.0000e+00, 0.0000e+00, 1.0000e+00, 0.0000e+00,
1.0000e+00, 0.0000e+00, 1.0000e+00],
[ 8.4147e-01, 5.4030e-01, 9.9833e-02, 9.9500e-01, 9.9998e-03,
9.9995e-01, 1.0000e-03, 1.0000e+00],
[ 9.0930e-01, -4.1615e-01, 1.9867e-01, 9.8007e-01, 1.9999e-02,
9.9980e-01, 2.0000e-03, 1.0000e+00],
[ 1.4112e-01, -9.8999e-01, 2.9552e-01, 9.5534e-01, 2.9995e-02,
9.9955e-01, 3.0000e-03, 1.0000e+00]]])
tensor([[[ 0.0000e+00, 1.0000e+00, 0.0000e+00, 1.0000e+00, 0.0000e+00,
1.0000e+00, 0.0000e+00, 1.0000e+00],
[ 8.4147e-01, 5.4030e-01, 9.9833e-02, 9.9500e-01, 9.9998e-03,
9.9995e-01, 1.0000e-03, 1.0000e+00],
[ 9.0930e-01, -4.1615e-01, 1.9867e-01, 9.8007e-01, 1.9999e-02,
9.9980e-01, 2.0000e-03, 1.0000e+00],
[ 1.4112e-01, -9.8999e-01, 2.9552e-01, 9.5534e-01, 2.9995e-02,
9.9955e-01, 3.0000e-03, 1.0000e+00]],
[[ 0.0000e+00, 1.0000e+00, 0.0000e+00, 1.0000e+00, 0.0000e+00,
1.0000e+00, 0.0000e+00, 1.0000e+00],
[ 8.4147e-01, 5.4030e-01, 9.9833e-02, 9.9500e-01, 9.9998e-03,
9.9995e-01, 1.0000e-03, 1.0000e+00],
[ 9.0930e-01, -4.1615e-01, 1.9867e-01, 9.8007e-01, 1.9999e-02,
9.9980e-01, 2.0000e-03, 1.0000e+00],
[ 1.4112e-01, -9.8999e-01, 2.9552e-01, 9.5534e-01, 2.9995e-02,
9.9955e-01, 3.0000e-03, 1.0000e+00]]])
2.4 构造encoder的self-attention mask
Step 4:因为句子的长度不一,于是我们会用padding去补0,之后便可得到有效位置矩阵。现在我们需要去得到有效矩阵,于是我们通过torch.bmm将有效位置矩阵与有效位置矩阵的转置矩阵的1,2维进行相乘(0维是batch维,不参与运算),便可得到有效矩阵。
valid_encoder_pos = torch.unsqueeze(torch.cat([torch.unsqueeze(F.pad(torch.ones(L), (0, max(src_len) - L)), 0)
for L in src_len]), 2)
valid_encoder_pos_matrix = torch.bmm(valid_encoder_pos, valid_encoder_pos.transpose(1, 2))
print(valid_encoder_pos_matrix)
输出有效矩阵
tensor([[[1., 1., 0., 0.],
[1., 1., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]],
[[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]]])
我们用1减去有效矩阵,并将其赋成bool型便可得到无效矩阵。
invalid_encoder_pos_matrix = 1 - valid_encoder_pos_matrix
mask_encoder_self_attention = invalid_encoder_pos_matrix.to(torch.bool)
print(invalid_encoder_pos_matrix)
print(mask_encoder_self_attention)
输出无效矩阵
tensor([[[False, False, True, True],
[False, False, True, True],
[ True, True, True, True],
[ True, True, True, True]],
[[False, False, False, False],
[False, False, False, False],
[False, False, False, False],
[False, False, False, False]]])
通过softmax得到mask矩阵。
score = torch.randn(batch_size, max(src_len), max(src_len))
masked_score = score.masked_fill(mask_encoder_self_attention, -1e9)
prob = F.softmax(masked_score, -1)
print(src_len)
print(score)
print(masked_score)
print(prob)
查看输出结果
tensor([2, 4], dtype=torch.int32)
tensor([[[-0.2043, -0.3917, -1.0137, -1.1826],
[-0.0821, 0.7781, -1.1928, 0.2586],
[-0.2179, 0.8631, -0.9092, 0.0432],
[ 0.3567, 1.0154, -1.0005, 0.2797]],
[[-0.9328, -0.6068, 1.0793, 1.0886],
[-0.8354, 0.6814, 1.3121, 1.2134],
[ 2.0781, -0.4271, -2.4216, 0.0345],
[-0.9104, -1.5460, 0.7630, 0.5593]]])
tensor([[[-2.0433e-01, -3.9166e-01, -1.0000e+09, -1.0000e+09],
[-8.2061e-02, 7.7813e-01, -1.0000e+09, -1.0000e+09],
[-1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09],
[-1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09]],
[[-9.3281e-01, -6.0677e-01, 1.0793e+00, 1.0886e+00],
[-8.3541e-01, 6.8140e-01, 1.3121e+00, 1.2134e+00],
[ 2.0781e+00, -4.2715e-01, -2.4216e+00, 3.4491e-02],
[-9.1038e-01, -1.5460e+00, 7.6298e-01, 5.5926e-01]]])
tensor([[[0.5467, 0.4533, 0.0000, 0.0000],
[0.2973, 0.7027, 0.0000, 0.0000],
[0.2500, 0.2500, 0.2500, 0.2500],
[0.2500, 0.2500, 0.2500, 0.2500]],
[[0.0574, 0.0796, 0.4295, 0.4335],
[0.0457, 0.2083, 0.3914, 0.3546],
[0.8181, 0.0668, 0.0091, 0.1060],
[0.0892, 0.0473, 0.4756, 0.3879]]])
2.5 构造intra-attention的mask
这里的步骤和Step 4差不多,但是要注意Q @ K ^ T,即decoder Q与encoder K ^ T的相关有效性。
valid_decoder_pos = torch.unsqueeze(torch.cat([torch.unsqueeze(F.pad(torch.ones(L), (0, max(tgt_len) - L)), 0)
for L in tgt_len]), 2)
valid_cross_pos_matrix = torch.bmm(valid_decoder_pos, valid_encoder_pos.transpose(1, 2))
invalid_cross_pos_matrix = 1 - valid_cross_pos_matrix
mask_cross_attention = invalid_cross_pos_matrix.to(torch.bool)
print(valid_cross_pos_matrix)
print(invalid_cross_pos_matrix)
print(mask_cross_attention)
查看输出结果
tensor([[[1., 1., 0., 0.],
[1., 1., 0., 0.],
[1., 1., 0., 0.],
[1., 1., 0., 0.]],
[[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.],
[0., 0., 0., 0.]]])
tensor([[[0., 0., 1., 1.],
[0., 0., 1., 1.],
[0., 0., 1., 1.],
[0., 0., 1., 1.]],
[[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.],
[1., 1., 1., 1.]]])
tensor([[[False, False, True, True],
[False, False, True, True],
[False, False, True, True],
[False, False, True, True]],
[[False, False, False, False],
[False, False, False, False],
[False, False, False, False],
[ True, True, True, True]]])
2.6 构成decoder self-attention的mask
这里的步骤和Step 4差不多,但是这里用到torch.tril生成三角矩阵,并且对行和列都进行了补0。
valid_decoder_tri_matrix = torch.cat([torch.unsqueeze(F.pad(torch.tril(torch.ones((L, L))),
(0, max(tgt_len) - L, 0, max(tgt_len) - L)), 0)
for L in tgt_len])
invalid_decoder_tri_matrix = 1 - valid_decoder_tri_matrix
invalid_decoder_tri_matrix = invalid_decoder_tri_matrix.to(torch.bool)
print(valid_decoder_tri_matrix)
print(invalid_decoder_tri_matrix)
查看三角矩阵
tensor([[[1., 0., 0., 0.],
[1., 1., 0., 0.],
[1., 1., 1., 0.],
[1., 1., 1., 1.]],
[[1., 0., 0., 0.],
[1., 1., 0., 0.],
[1., 1., 1., 0.],
[0., 0., 0., 0.]]])
tensor([[[False, True, True, True],
[False, False, True, True],
[False, False, False, True],
[False, False, False, False]],
[[False, True, True, True],
[False, False, True, True],
[False, False, False, True],
[ True, True, True, True]]])
通过无效矩阵做softmax,得到mask。
score = torch.randn(batch_size, max(tgt_len), max(tgt_len))
masked_score = score.masked_fill(invalid_decoder_tri_matrix, -1e9)
prob = F.softmax(masked_score, -1)
print(tgt_len)
print(prob)
输出得到的mask
tensor([4, 3], dtype=torch.int32)
tensor([[[1.0000, 0.0000, 0.0000, 0.0000],
[0.3802, 0.6198, 0.0000, 0.0000],
[0.6869, 0.2416, 0.0716, 0.0000],
[0.1204, 0.1475, 0.1840, 0.5481]],
[[1.0000, 0.0000, 0.0000, 0.0000],
[0.5099, 0.4901, 0.0000, 0.0000],
[0.1156, 0.8410, 0.0434, 0.0000],
[0.2500, 0.2500, 0.2500, 0.2500]]])
最后一行是因为补了一行的0,然后概率相等,各自都是0.2500。
2.7 构建scaled self-attention
def scaled_dot_product_attention(Q, K, V, attn_mask):
# shape of Q,K,V : (batch_size*num_head. seq_len, model_dim/num_head)
score = torch.bmm(Q, K.transpose(-2, -1)/torch.sqrt(model_dim))
masked_score = score.masked_fill(attn_mask, -1e9)
prob = F.softmax(masked_score, -1)
context = torch.bmm(prob, V)
return context
总结
在本周的学习中,主要学习了Transformer模型,是一种避免循环的模型结构,完全依赖于注意力机制对输入输出的全局依赖关系进行建模。Transformer模型的优势是突破了 RNN 模型不能并行计算的限制;相比CNN来说,计算两个位置之间的关联所需的操作次数不随距离增长;自注意力可以产生更具可解释性的模型。本周对论文只是进行简单地阅读,在下周会对论文进行详细地阅读并理解,并对Transformer模型进行详细地解释说明。