英文题目:Distilling the Knowledge in a Neural Network
中文题目:神经网络知识蒸馏
论文地址:https://arxiv.org/pdf/1503.02531.pdf
领域:深度学习
发表时间:2015
作者:Geoffrey Hinton,谷歌
出处:NIPS
被引量:6972
阅读时间:2022.09.21
读后感
这是最早提出蒸馏模型的文章,它训练老师Teacher/学生Student两个模型,首先训练大而全的Teacher,然后用Teacher蒸馏出小而精的Student,S不仅学习T的对错判断,还学到更多细节,比如为什么错(错的离不离谱)。
介绍
作者提出训练和部署的模型未必是同一模型。大而复杂的模型效果(后简称Teacher/T)好,但相对复杂,预测时间长,占空间更大。作者提出如何把集成模型或大模型用一个小模型(后简称Student/S)实现。训练阶段产出大而全的模型,然后用蒸馏技术提炼小模型,以便部署。
和压缩参数相比,在输入输出之间建立新的映射可能是更好的模型瘦身方法。一般建模方法是:模型主要学习正例为什么分对,让负例概率越小越好。而实际上,负例的概率应该是有差异的。比如在识别宝马汽车时,垃圾车和胡萝卜都是负例,但垃圾车更像宝马。这一问题可能影响了模型对新数据的泛化。比如:在数据识别MNIST任务中,有时2看起来更像3,有时更像7,而像3的概率是10-6,像7的概率是10-9,差别非常微小。之前的方法是用对数修改Softmax作为损失函数,来计算小模型与大模型的误差。
文中进一步提出了“蒸馏”方法,以得到更丰富的信息,通过提升Softmax的“温度”,直到产生合理的软目标。
小模型可以使用未标注的数据训练(大模型打标签),也可以使用训练集数据训练,实验证明,使用训练集数据,并结合软目标和实际的预测损失效果更好。
方法
对于多分类问题,计算每个类的概率qi如下:
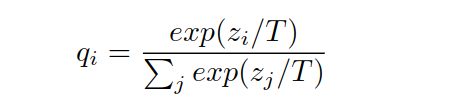
其中T是温度参数,一般设成1,设成大于1时,则产生较软的概率分布。下面看看软目标与硬目标的差异:
import numpy as np
def softmax(x,T=1):
f_x = np.exp(x/T) / np.sum(np.exp(x/T), axis=1, keepdims=True)
return f_x
print(softmax(np.array([[1,4,5]]), T=1))
#[[0.01321289 0.26538793 0.72139918]]
print(softmax(np.array([[1,4,5]]), T=3))
#[[0.13312123 0.36186103 0.50501774]]
print(softmax(np.array([[1,4,5]]), T=10))
#[[0.26030255 0.35137169 0.38832577]]
可以看到T=1时为硬目标,虽然4与5很相近,但概率差异很,调参时也将更重视最终的选择5;而T=10时,各项的得分又过于相近。
最终的损失函数由两部分组成,第一部分是用同样的温度训练的T模型和S模型两者间的差异;第二部分是S模型对实例真实标签的预测损失,此处的温度使用1,实验结果是对第二部分应用较低权重效果更好。
梯度计算
设zi是S模型结果,产生软概率qi,vi是T模型的结果,产生软概率pi,蒸馏模型的梯度计算如下:
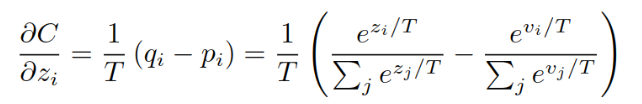
如果温度很高,根据e^x的泰勒展开,后面项忽略不计,只保留前两项,变成:
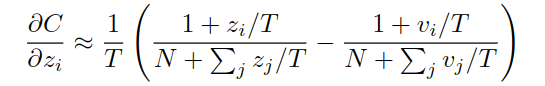
再假设所有样本的预测均值为0,
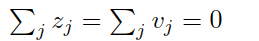
则有:
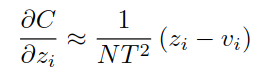
因此在温度T较高时,用梯度往回推损失函数就是最小化z和v的均方误差,即蒸馏的目标是让z和v尽量一致,对正负例给予相似的关注,S模型能学到更多细节。而当温度低时,则如同普通Softmax,相对不重视负例。实验表明,当S模型太小,无法捕捉到T模型的所有知识时,中等温度是一种折中。