[人工智能]图像处理与机器视觉_第三篇

前言

本篇讲的是图像的几何变换的知识，其中具有一些代码实现。

一、图像几何变换

由于拍摄图像的角度、距离等原因，可能会需要对图像进行适当的几何变换。
几何变换又称为空间变换，是将一幅图像中的坐标位置映射到另外一幅图像中的新坐标位置。

二、解决几何变换问题的思路

一般要考虑原图像中的某个像素点的坐标$(x_0,y_0)$和此像素点映射到新图像中的新坐标$(x_1,y_1)$之间的关系。可由下式描述：$x_1=f_1(x_0,y_0)$；$y_1=f_2(x_0,y_0)$。

三、图像镜像

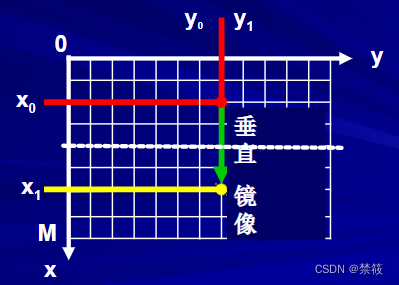
垂直镜像：图像的上半部分和下半部分以图像水平中轴线为中心轴进行对称变换。以下图为例：

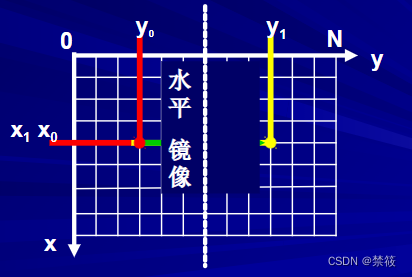
水平镜像：图像的左半部分和右半部分以图像竖直中轴线为中心轴进行对称变换。以下图为例：

3.1、水平镜像的变换公式

$(x_0,y_0)$是原图像上的点，中心轴如图所示，水平镜像对应的新坐标点为：$x_1=x_0$；$y_1=N?y_0$；

水平镜像的变换矩阵：

代码示例如下：

read_image(Image, '图片路径')
mirror_image(Image, ImageMirror, 'column')

3.2、垂直镜像的变换公式

$(x_0,y_0)$是原图像上的点，中心轴如图所示，水平镜像对应的新坐标点为：$x_1=M?x_0$；$y_1=y_0$；

垂直镜像的变换矩阵：

代码示例如下：

read_image(Image, '图片路径')
mirror_image(Image, ImageMirror, 'row')

PS：要注意x轴和y轴分别是什么坐标轴，我的例子是x轴是纵轴、y轴是横轴，所以如果x、y轴有变化相应的公式以及变换矩阵也有变化。

四、图像转置

4.1、图像转置的公式

图像转置即行列互换，$(x_0,y_0)$是原图像上的点，转置后对应的新坐标点为：$x_1=y_0$；$y_1=x_0$；注意：图像尺寸有可能改变。

4.2、图像转置的程序实现

代码示例如下：

read_image(Image, '图像路径')
mirror_image(Image, ImageMirror, 'diagonal')

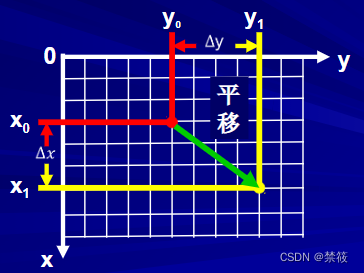
五、图像平移

$(x_0,y_0)$是原图像上的点，图像水平平移量为$\Delta y$，垂直平移量为$\Delta x$，如图所示。
平移后的新坐标点为：$x_1=x_0+\Delta x$；$y_1=y_0+\Delta y$；

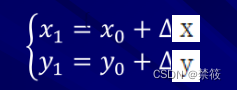
图像平移变换式的矩阵形式为：

以下为图像平移样例：

代码示例如下：

// 对图像进行右下移位
read_image(Image, '图像路径')
get_image_size(Image, Width, Height)
hom_mat2d_identity(HomMat2DIdentity)
hom_mat2d_translate(HomMat2DIdentity, 60, 60, HomMat2DTranslate)
affine_trans_image(Image, ImageAffinTrans, HomMat2DTranslate, 'weighted', 'false')

结果如下：

矩阵形式：

其中，关于最后一个函数的解释：

六、图像缩放

图像比例缩放变换：指将给定的图像在x轴方向按比例缩放r倍，在y轴方向上按比例缩放r倍，从而获得一幅新的图像。比例缩放前后两点$P_0(x_0,y_0)$、$P(x,y)$之间的关系可以表示为：$$\{\begin{array}{l}x=r{x}_0\\ y=r{y}_0\end{array}$$

矩阵形式：$$?\begin{array}{c}x\\ y\\ 1\end{array}?=?\begin{array}{ccc}r& 0& 0\\ 0& r& 0\\ 0& 0& 1\end{array}??\begin{array}{c}{x}_0\\ y_0\\ 1\end{array}?$$
其中：$r>1$，放大；$0<r<1$，缩小

6.1、缩小

目的：
1、使缩小后的图像符合显示区域的大小要求；
2、生成原图像的缩略图。

图像的缩小操作，是在现有的信息里挑选所需要的有用信息。

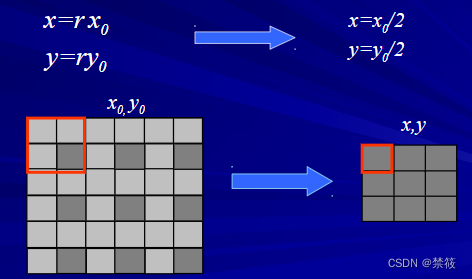
如果图像按任意比例缩小，则需要计算所需选择的行列。

图像缩小实现算法：

图像缩小例题：

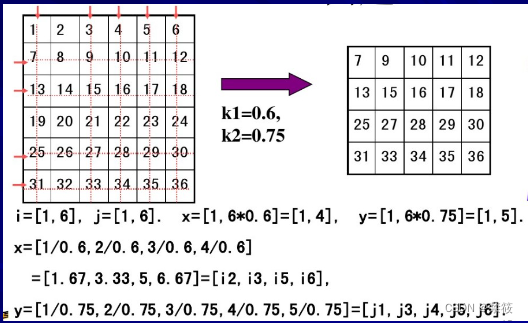
使用四舍五入策略

6.2、放大

图像的放大操作，需对尺寸放大后所多出来的空格填入适当的值，这是信息的估计问题，所以较图像的缩小要难一些。

图像放大一般分为按比例放大和不按比例放大两种：

• 按比例放大： 如果需要将原图像放大k倍，则将一个像素值填在新图像的$k\times k$的子块中。
• 任意不按比例放大： 这种操作由于x方向和y方向的放大倍数不同一定带来图像的几何畸变。
• 图像放大倍数太大，会出现马赛克效应。

图像放大实现思路：

最简单的思想是如果需要将原图像放大为k倍，则将原图像中的每个像素值，填在新图像中对应的$k\times k$大小的子块中。

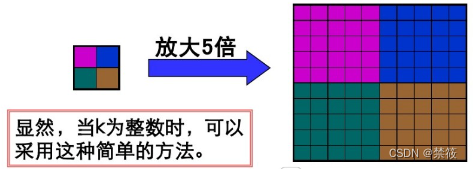
图像放大实现方法：

设原图像大小为$M\times N$，放大为$k_{1}M\times k_{2}N,(k_1>1,k_2>1)$。算法步骤如下：

• 设旧图像是$F(i,j),i=1,2,...,M,j=1,2,...,N$；新图像是$G(x,y),x=1,2,...,k_{1}M,y=1,2,...,k_{2}N$。
• $G(x,y)=F(c_1?x,c_2?y),c_1=\frac{1}{k_1},c_2=\frac{1}{k_2}$
  

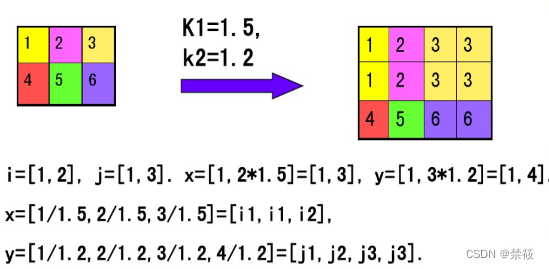
图像的成倍放大效果示例：

图像大比例放大时的马赛克效应：

6.3、灰度级插值方法

思考问题：
如果放大倍数太大，按照前面的方法处理会出现马赛克效应。如果这个问题交给你，有没有办法解决？或者想办法至少使之有所改善？

• 灰度级插值法
  • 最邻近插值法
  • 双线性插值法（一阶插值）
  • 高阶插值

最邻近插值法（nearest neighbor interpolation)

• 最简单的插值方法是最邻近插值，即选择离它所映射到的位置最近的输入像素的灰度值为插值结果。
• 数学表示为：$f(x)=f(x_k)$
• $\frac{1}{2}(x_{k?1}+x_k)<x<\frac{1}{2}(x_k+x_{k+1})$

双线性插值（bilinear interpolation)

• 双线性插值法是对最邻近插值法的一种改进，即用线性内插方法，根据点的四个相邻点的灰度值，分别在x和y方向上进行两次线性插值，如下图：
  
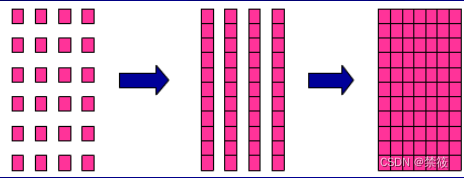
  基本算法思想：
• 假设输出图像的宽度为W，高度为H；
• 输入图像的宽度为w，高度为h；
• 要将输入图像的尺度拉伸或压缩变换至输出图像的尺度；
• 按照线性插值的方法，将输入图像的宽度方向分为W等份，高度方向分为H等份，那么输出图像中任意一点$(u_0,v_0)$的灰度值就应该由输入图像中四点$(u,v)$、$(u+1,v)$、$(u,v+1)$和$(u+1,v+1)$的灰度值来确定。
  
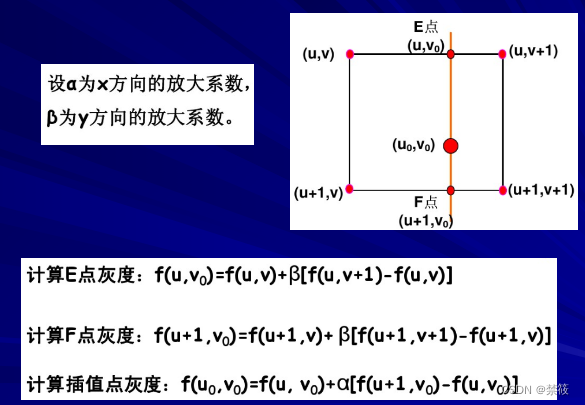
  横坐标轴是y轴
  按比例放大图像：
  

插值算法示例：

代码如下：

zoom_image_size(Image, ImageZoom, Width1, Height1, Interpolation)
/*参数Interpolation用于指定插值的方法，几种可选值为：
'nearest_neighbor',最邻近插值法
'constant',（默认值）
'bilinear',双线性插值
'weighted'
*/

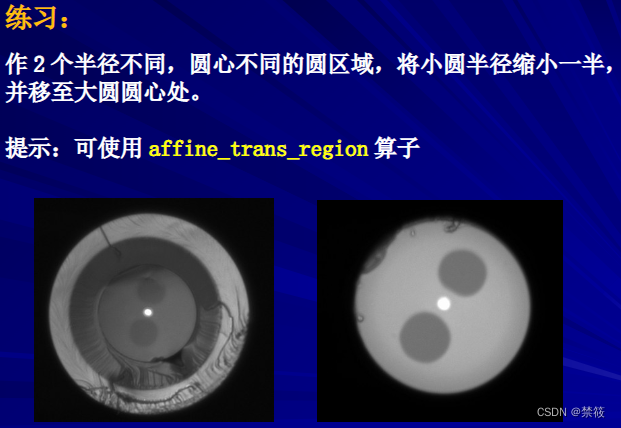
七、图像的旋转变换

一般图像的旋转是以图像的中心为原点，旋转一定的角度，即将图像上的所有像素都旋转一个相同的角度。

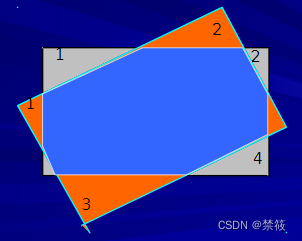
图像的旋转变换也可用矩阵变换表示。设点$P_0(x_0,y_0)$旋转角$\beta$后的对应点为$P(x,y)$。如下图所示：

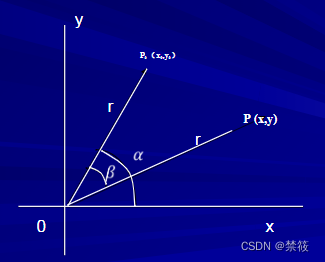
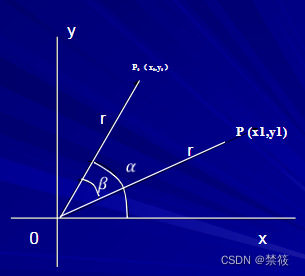
旋转前：$$\{\begin{array}{l}{x}_0=rcos\alpha \\ y_0=rsin\alpha \end{array}$$
旋转后：$$\{\begin{array}{l}{x}_1=rcos(\alpha ?\beta )=rcos\alpha cos\beta +rsin\alpha sin\beta \\ y_1=rsin(\alpha ?\beta )=rsin\alpha cos\beta ?rcos\alpha sin\beta \end{array}$$
代入得：$$\{\begin{array}{l}{x}_1=x_{0}cos\beta +y_{0}sin\beta \\ y_1=?x_{0}sin\beta +y_{0}cos\beta \end{array}$$
矩阵形式为：$$?\begin{array}{c}{x}_1\\ y_1\\ 1\end{array}?=?\begin{array}{ccc}cos\beta & sin\beta & 0\\ ?sin\beta & cos\beta & 0\\ 0& 0& 1\end{array}??\begin{array}{c}{x}_0\\ y_0\\ 1\end{array}?$$

代码如下：

rotate_image(Image, ImageRotate, Phi, Interpolation)
//Phi：角度

图像示例：

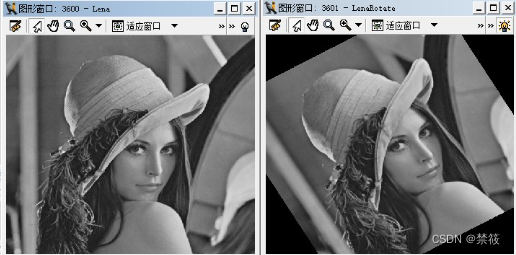
代码示例如下：

// 以中心为基准点进行旋转
rotate_image(Image, ImageRotate, 45, 'constant')

//以（200，200）为基准点进行旋转
hom_mat2d_identity(HomMat2DIdentity)
hom_mat2d_rotate(HomMat2DIdentity, 0.78, 200, 200, HomMat2DRotate)
affine_trans_image(Image, ImageAffinTrans, HomMat2DRotate, 'weighted', 'false')

结束！