[人工智能]图神经网络对抗攻击（图注入攻击）

paper1 :TDGIA(Effective Injection Attacks on Graph Neural Networks) part1

论文下载

Abstract

图神经网络在各种实际应用中都取得了良好的性能。然而，最近的研究发现，GNN容易受到对抗攻击。本文研究了最近引入的一种针对**图注入攻击（GIA）**的真实攻击场景。在GIA场景中，攻击者无法修改输入图的现有连接结构或节点属性，而是通过向其中注入攻击节点来执行攻击。*我们分析了GNN在GIA设置下的拓扑脆弱性，并在此基础上提出了用于有效注入攻击的拓扑缺陷图注入攻击（TDGIA）*TDGIA首先引入拓扑脆弱边选择策略来选择原始节点与注入节点连接。然后设计平滑特征优化目标，为注入节点生成特征。大规模数据集上的大量实验表明，TDGIA在攻击数十个防御GNN模型时，能够持续且显著的优于各种攻击基线。值得注意的是，在KDD-CUP2020提交的数百份文件中，TDGIA的导致的目标GNN性能下降是最佳攻击解决方案造成的损害两倍多。

1、Introduction

近年来，图机器学习被广泛用于结构化和关系数据建模。特别是图神经网络（GNN）的出现为不同的图应用提供了有前景的结果，例如节点分类、社会推荐和药物发现。

尽管取得了令人兴奋的进展，但研究表明，神经网络通常容易受到对抗攻击，在这种情况下，输入上为不可察觉但故意设计的扰动可能会导致错误的预测。对一般神经网络的攻击通常侧重于修改输入实例的属性/特征，例如图像单个像素的轻微扰动。特别是，对抗攻击也可以用于图形结构的输入、需要专门的策略来探索底层的特定缺陷。

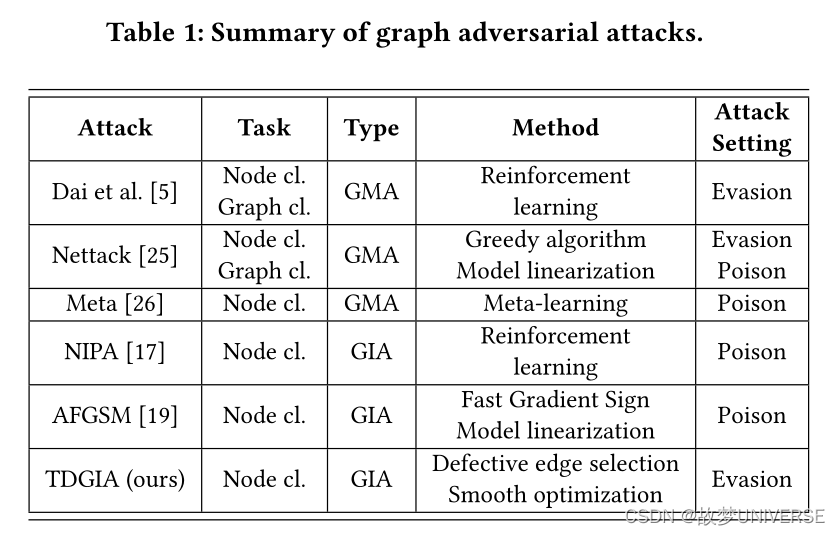
对GNN的早期攻击通常遵循图修改攻击（GMA）的设置，如图1（a）所示：给定一个具有属性的输入图形，攻击者可以直接修改其节点（红色连接）和现有节点（红色节点）属性之间的连接。然而在现实场景中，攻击者获得修改现有数据的权限通常是不现实的。以引文图为例，当论文发表时，它会自动形成，这使得以后更改一篇出版物的引文和属性实际上是很困难的。但相对容易的是，向现有引文图中注入新的节点和连接，例如，通过“发布”假论文来误导GNN的预测。

具体而言，KDD-CUP2020中的GIA人物规定如下：（1）黑盒攻击，攻击者无法访问目标GNN模型或目标节点的正确标签；（2）逃逸攻击，攻击只能在测试阶段执行。GIA设置提出了GMA没有面临的独特挑战，例如如何将现有节点与注入节点连接起来，以及如何从头开始为注入节点生成特征。

contributions 在这项工作中，研究了黑盒和逃逸攻击设置下的GIA问题，目标是设计一个有效的注入攻击框架，该框架可以最好的愚弄目标GNN模型，从而降低其预测能力。为了理解这个问题及其挑战，对GNN在图注入攻击下的脆弱性进行了深入分析，并表明GNN作为non-structural-ignorant模型，是GIA可攻击的。基于此，提出了拓扑脆弱图注入攻击（TDGIA）（见图1（b））.TDCIA由拓扑脆弱边选择和注入节点属性生成的平滑对抗优化两个模块组成，与GIA问题的设置对应。利用原始图的拓扑脆弱来检测最有助于攻击的现有节点，然后以顺序方式注入围绕这些节点的新节点。在此基础上，设计了一个平滑损失函数来优化节点的特征，以最小化目标GNN模型的性能。

2、Related works

Adversarial Attacks on Neural Networks

首先是针对基于深度学习的对抗性示例现象在计算机视觉中发现。在图像中添加微笑和不可察觉的扰动可以显著改变深层神经网络的预测。提出了快速梯度符号法，利用训练神经网络的梯度来产生这种扰动。此后，提出了更先进的攻击方法。对抗攻击也在更广泛的领域发展，例如自然语言处理或语音识别。如今，对抗性攻击已经成为神经网络的主要威胁之一。

Adversarial Attacks on GNNs

由于存在对抗性示例，图学习算法的脆弱性也被揭示出来。通过修改图形结构数据的特征和边，攻击可以显著降低GNN模型的性能。针对节点分类和图分类任务提出了一种基于强化学习的攻击。这种攻击只会修改图形的结构。Nettack的提出，是对属性图的第一次对抗性攻击。它表明，在图的边和特征上只有很少的扰动对GCN这样的模型是及其有害的。Nettack在不明显扰动的约束下使用贪婪近似方案，并结合快速计算。此外，也提出了一种通过元学习对GNN 进行投毒攻击，即元攻击，它只修改了图的一小部分，但仍然可以显著降低GNN在节点分类任务上的性能。

也有文章研究了一种更现实的场景，即图注入攻击（GIA），它注入新的恶意节点，而不是修改原始图。

3、Problem Definition

一般来说，有两种类型的图对抗攻击：图修改攻击（GMA）和图注入攻击（GIA），本文的重点是图注入攻击，将攻击问题形式化并引入攻击设置。

图对抗攻击的问题首先是在Nettack中形式化，称之为图修改攻击，具体来说，定义一个属性图$G=(A,F)$, $A\in R^{N\times N}$ 是它$N$个节点的邻接矩阵，$F\in R^{N\times D}$是$D$维节点特征， M : G → { 1 , 2 , … , C } N M:G\to{\{1,2,\ldots ,C\}}^N M:G→{1,2,…,C}N预测在$G$中$N$个节点的标签，并将其预测表示为$M(G)$.GMA的目标是通过修改原始图$G$,最小化一组目标节点$\mathcal{T}$上$M$的正确预测数量：

min ? G ′ ∣ { M ( G ′ ) i = y i , i ∈ T } ∣ ?s.t.? G ′ = ( A ′ , F ′ ) , f Δ A ( A ′ ? A ) + f Δ F ( F ′ ? F ) ≤ Δ \begin{array} { l } \min _ { \mathrm { G } ^ { \prime } } \left| \left\{ \mathcal { M } \left( \mathrm { G } ^ { \prime } \right) _ { i } = y _ { i } , i \in \mathcal { T } \right\} \right| \\ \text { s.t. } \mathrm { G } ^ { \prime } = \left( \mathrm { A } ^ { \prime } , \mathrm { F } ^ { \prime } \right) , f _ { \Delta _ { \mathrm { A } } } \left( \mathrm { A } ^ { \prime } - \mathbf { A } \right) + f _ { \Delta _ { \mathrm { F } } } \left( \mathrm { F } ^ { \prime } - \mathrm { F } \right) \leq \Delta \end{array} minG′?∣{M(G′)i?=yi?,i∈T}∣?s.t.?G′=(A′,F′),fΔA??(A′?A)+fΔF??(F′?F)≤Δ?

$G^{\prime }$是修改后的图形，$y_i$是节点的真实标签，$f_{{\Delta }_{\mathrm{A}}}$和$f_{{\Delta }_{\mathrm{F}}}$是衡量修改规模的预定义函数。约束$\Delta$确保攻击只能轻微修改原图。

Graph Injection Attacks

不是GMA对$G^{\prime }$结构和属性的修改，GIA直接注入$N_I$,将新节点添加到$G$中，同时保留原始边和$N$个节点的属性不变。形式上，GIA构造$G^{\prime }=(A^{\prime },F^{\prime })$通过
$$\begin{array}{c}{\mathbf{A}}^{\prime }=\left[\begin{array}{cc}\mathbf{A}& {\mathbf{V}}_I\\ {\mathbf{V}}_I^T& {\mathbf{A}}_I\end{array}\right],\mathbf{A}\in {\mathbb{R}}^{N\times N},{\mathbf{V}}_I\in {\mathbb{R}}^{N\times N_I},{\mathbf{A}}_I\in {\mathbb{R}}^{N_I\times N_I}\\ {\mathbf{F}}^{\prime }=\left[\begin{array}{c}\mathbf{F}\\ {\mathbf{F}}_I\end{array}\right],\mathbf{F}\in {\mathbb{R}}^{N\times D},{\mathbf{F}}_I\in {\mathbb{R}}^{N_I\times D}\end{array}$$

${\mathbf{A}}_I$是注入节点的邻接矩阵，${\mathbf{V}}_I$是一个矩阵，表示$G$的原始节点与注入节点之间的边，${\mathbf{F}}_I$是注入节点的特征矩阵。GIA的目标可以形式化为：
min ? G ′ ∣ { M ( G ′ ) i = y i , i ∈ T } ∣ ?s.t.? G ′ = ( A ′ , F ′ ) , N I ≤ b , deg ? ( v ) v ∈ I ≤ d , ∥ F I ∥ ≤ Δ F \begin{array} { l } \min _ { \mathrm { G } ^ { \prime } } \left| \left\{ \mathcal { M } \left( \mathrm { G } ^ { \prime } \right) _ { i } = y _ { i } , i \in \mathcal { T } \right\} \right| \\ \text { s.t. } \mathrm { G } ^ { \prime } = \left( \mathrm { A } ^ { \prime } , \mathrm { F } ^ { \prime } \right) , N _ { I } \leq b , \operatorname { deg } ( v ) _ { v \in I } \leq d , \left\| \mathbf { F } _ { I } \right\| \leq \Delta _ { F } \end{array} minG′?∣{M(G′)i?=yi?,i∈T}∣?s.t.?G′=(A′,F′),NI?≤b,deg(v)v∈I?≤d,∥FI?∥≤ΔF??

$I$是注入节点的集合，$N_I$受预算$b$限制，每个注入节点的度受预算$d$限制，注入特征的范数受${\Delta }_F$的限制。这些约束是为了防御尽可能不注意GIA。

The Attack Settings of GIA

GIA最近受到了广泛的关注，并成为KDD-CUP2020竞赛的任务之一，考虑到它在现实世界场景中的广泛意义，遵循在比赛中使用的相同设置，即黑盒和逃逸攻击。

黑盒攻击。在黑盒设置中，攻击无法访问目标模型$M$,包括其架构、参数和防御机制。然而攻击可以访问原始属性图$G=(A,F)$以及训练和验证节点的标签，但不能访问要攻击的节点。

逃逸攻击。GIA遵循逃逸攻击设置，即在测试阶段只对目标模型执行攻击。这使的它不同于投毒攻击，在投毒攻击中，目标模型被重新约束在受攻击的图上。

The GIA Process

由于黑盒和逃逸设置，GIA需要借助代理模型进行迁移攻击。首先，训练代理模型；其次，对该模型进行注入攻击；最后，攻击迁移到一个或多个目标模型上。

为了处理大规模数据集，GIA可以根据其定义分为两个步骤。首先，生成现有节点和注入节点$({\mathbf{A}}_I,V)$之间的边；其次，优化注入节点的特征。这种分解可以大大降低复杂性，并使GIA适用于大型图。

目标模型可以$M$可以是任何图机器学习模型，本文的重点是以图神经网络为目标模型。