什么是RNN
循环神经网络RNN用于语言分析, 序列化数据。
序列数据
有一组序列数据 data 0,1,2,3.
在当预测 result0 的时候,我们基于的是 data0, 同样在预测其他数据的时候, 我们也都只单单基于单个的数据. 每次使用的神经网络都是同一个 NN.
但data 0123 之间是有关联顺序的,普通神经网络结构无法让nn了解这些数据之间的关系
处理序列数据的神经网络
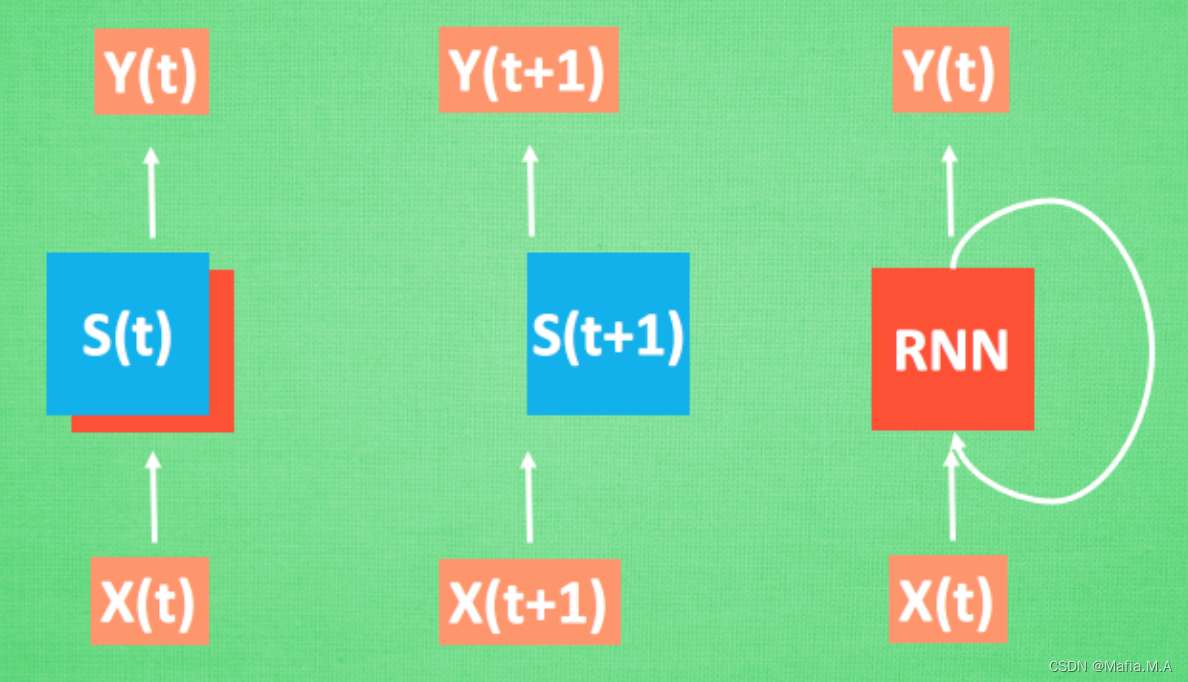
每次 RNN 运算完之后都会产生一个对于当前状态的描述 , state. 我们用简写 S( t) 代替, 然后这个 RNN开始分析 x(t+1) , 他会根据 x(t+1)产生s(t+1), 不过此时 y(t+1) 是由 s(t) 和 s(t+1) 共同创造的. 所以我们通常看到的 RNN 也可以表达成这种样子.
RNN弊端
RNN是在有顺序的数据上进行学习的,最开始的数据要经过最长时间才能抵达最后,然后计算得到误差,而且在 反向传递 得到的误差的时候, 在每一步都会乘以一个自己的参数 W。
普通 RNN 没有办法回忆起久远记忆的原因:
- 如果 W<1 ,比如0.9. 这个0.9 不断乘以误差, 误差传到初始时间点也会是一个接近于零的数, 所以对于初始时刻, 误差相当于就消失了
- 如果 W >1 ,比如1.1 不断累乘, 则到最后变成了无穷大的数, RNN被这无穷大的数撑死了, 这种情况叫做梯度爆炸, Gradient exploding
LSTM
LSTM 和普通 RNN 相比, 多出了三个控制器. (输入控制, 输出控制, 忘记控制)
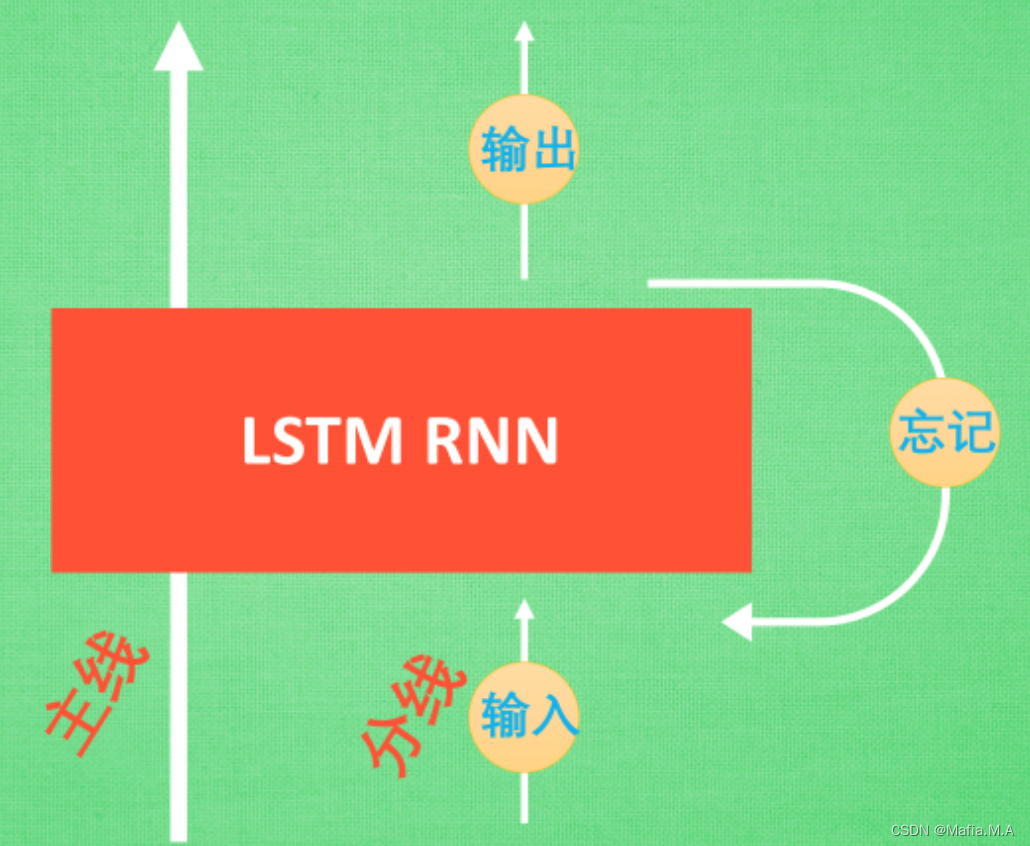
- 主线(控制全局的记忆)
- 分线(原本的 RNN 体系)
- 三个控制器都是在原始的 RNN 体系上:
a.输入方面:如果此时的分线剧情对于剧终结果十分重要, 输入控制就会将这个分线剧情按重要程度 写入主线剧情 进行分析
b.忘记方面:如果此时的分线剧情更改了我们对之前剧情的想法, 那么忘记控制就会将之前的某些主线剧情忘记, 按比例替换成现在的新剧情
c.输出方面:输出控制会基于目前的主线剧情和分线剧情判断要输出的到底是什么
RNN_分类
"""
View more, visit my tutorial page: https://mofanpy.com/tutorials/
My Youtube Channel: https://www.youtube.com/user/MorvanZhou
Dependencies:
torch: 0.4
matplotlib
torchvision
"""
import torch
from torch import nn
import torchvision.datasets as dsets
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
# torch.manual_seed(1) # reproducible
# Hyper Parameters
EPOCH = 1 # 训练整批数据次数train the training data n times, to save time, we just train 1 epoch
BATCH_SIZE = 64
TIME_STEP = 28 # rnn 时间步数 / 图片高度 rnn time step / image height
INPUT_SIZE = 28 # rnn 每步输入值 / 图片每行像素 rnn input size / image width
LR = 0.01 # 学习效率 learning rate
DOWNLOAD_MNIST = True # set to True if haven't download the data
# Mnist digital dataset
# 下载训练所需要的数据集
train_data = dsets.MNIST(
root='./mnist/',
train=True, # this is training data
transform=transforms.ToTensor(), # Converts a PIL.Image or numpy.ndarray to
# torch.FloatTensor of shape (C x H x W) and normalize in the range [0.0, 1.0]
download=DOWNLOAD_MNIST, # download it if you don't have it
)
# plot one example
print(train_data.data.size()) # (60000, 28, 28)
print(train_data.targets.size()) # (60000)
# Data Loader for easy mini-batch return in training
# 准备训练集
train_loader = torch.utils.data.DataLoader(dataset=train_data, batch_size=BATCH_SIZE, shuffle=True)
# convert test data into Variable, pick 2000 samples to speed up testing
# 准备测试集
test_data = dsets.MNIST(root='./mnist/', train=False, transform=transforms.ToTensor())
test_x = test_data.data.type(torch.FloatTensor)[:2000]/255. # shape (2000, 28, 28) value in range(0,1)
test_y = test_data.targets.numpy()[:2000] # covert to numpy array
class RNN(nn.Module):
def __init__(self):
super(RNN, self).__init__()
self.rnn = nn.LSTM( # 使用LSTM效果比RNN好 if use nn.RNN(), it hardly learns
input_size=INPUT_SIZE, # 图片每行的数据像素点
hidden_size=64, # rnn hidden unit
num_layers=1, # 有几层RNN layers # number of rnn layer
batch_first=True, # input & output will has batch size as 1s dimension. e.g. (batch, time_step, input_size)
)
self.out = nn.Linear(64, 10) # 输出层,64(因为hidden大小为64),10(最后识别的是10个数字类别)
def forward(self, x):
# x shape (batch, time_step, input_size)
# r_out shape (batch, time_step, output_size)
# h_n shape (n_layers, batch, hidden_size)
# h_c shape (n_layers, batch, hidden_size)
r_out, (h_n, h_c) = self.rnn(x, None) # None 表示 hidden state 会用全0的 state None represents zero initial hidden state
# choose r_out at the last time step
# 选取最后一个时间点的 r_out 输出
# 这里 r_out[:, -1, :] 的值也是 h_n 的值
out = self.out(r_out[:, -1, :])
return out
rnn = RNN()
print(rnn)
optimizer = torch.optim.Adam(rnn.parameters(), lr=LR) # optimize all cnn parameters
loss_func = nn.CrossEntropyLoss() # the target label is not one-hotted
# training and testing
for epoch in range(EPOCH):
for step, (b_x, b_y) in enumerate(train_loader): # gives batch data
b_x = b_x.view(-1, 28, 28) # reshape x to (batch, time_step, input_size)
print(str(step) + ": " + str(b_x.size()))
output = rnn(b_x) # rnn output
loss = loss_func(output, b_y) # cross entropy loss
optimizer.zero_grad() # clear gradients for this training step
loss.backward() # backpropagation, compute gradients
optimizer.step() # apply gradients
if step % 50 == 0:
test_output = rnn(test_x) # (samples, time_step, input_size)
pred_y = torch.max(test_output, 1)[1].data.numpy()
accuracy = float((pred_y == test_y).astype(int).sum()) / float(test_y.size)
print('Epoch: ', epoch, '| train loss: %.4f' % loss.data.numpy(), '| test accuracy: %.2f' % accuracy)
# print 10 predictions from test data
test_output = rnn(test_x[:10].view(-1, 28, 28))
pred_y = torch.max(test_output, 1)[1].data.numpy()
print(pred_y, 'prediction number')
print(test_y[:10], 'real number')
RNN_回归
使用sin预测cos
"""
View more, visit my tutorial page: https://mofanpy.com/tutorials/
My Youtube Channel: https://www.youtube.com/user/MorvanZhou
Dependencies:
torch: 0.4
matplotlib
numpy
"""
import torch
from torch import nn
import numpy as np
import matplotlib
matplotlib.use('TkAgg')
import matplotlib.pyplot as plt
# torch.manual_seed(1) # reproducible
# Hyper Parameters
TIME_STEP = 10 # rnn time step
INPUT_SIZE = 1 # rnn input size
LR = 0.02 # learning rate
# show data
steps = np.linspace(0, np.pi * 2, 100, dtype=np.float32) # float32 for converting torch FloatTensor
print(steps.size)
x_np = np.sin(steps)
y_np = np.cos(steps)
# plt.plot(steps, y_np, 'r-', label='target (cos)')
# plt.plot(steps, x_np, 'b-', label='input (sin)')
# plt.legend(loc='best')
# plt.show()
class RNN(nn.Module):
def __init__(self):
super(RNN, self).__init__()
self.rnn = nn.RNN(
input_size=INPUT_SIZE,
hidden_size=32, # rnn hidden unit
num_layers=1, # number of rnn layer
batch_first=True, # input & output will has batch size as 1s dimension. e.g. (batch, time_step, input_size)
)
self.out = nn.Linear(32, 1)
# 因为 hidden state 是连续的, 所以我们要一直传递这一个 state
def forward(self, x, h_state):
# x (batch, time_step, input_size)
# h_state (n_layers, batch, hidden_size)
# r_out (batch, time_step, hidden_size)
r_out, h_state = self.rnn(x, h_state) # h_state 也要作为 RNN 的一个输入
print("r_out size: " + str(r_out.size()))
print(r_out.size(1))
outs = [] # save all predictions # 保存所有时间点的预测值
for time_step in range(r_out.size(1)): # calculate output for each time step
outs.append(self.out(r_out[:, time_step, :]))
print("outs size:" + str(outs.size()))
return torch.stack(outs, dim=1), h_state
# instead, for simplicity, you can replace above codes by follows
# r_out = r_out.view(-1, 32)
# outs = self.out(r_out)
# outs = outs.view(-1, TIME_STEP, 1)
# return outs, h_state
# or even simpler, since nn.Linear can accept inputs of any dimension
# and returns outputs with same dimension except for the last
# outs = self.out(r_out)
# return outs
rnn = RNN()
print(rnn)
optimizer = torch.optim.Adam(rnn.parameters(), lr=LR) # optimize all cnn parameters
loss_func = nn.MSELoss()
h_state = None # for initial hidden state
plt.figure(1, figsize=(12, 5))
plt.ion() # continuously plot
for step in range(100):
print("当前:" + str(step))
start, end = step * np.pi, (step + 1) * np.pi # time range
# use sin predicts cos
steps = np.linspace(start, end, TIME_STEP, dtype=np.float32,
endpoint=False) # float32 for converting torch FloatTensor
x_np = np.sin(steps)
y_np = np.cos(steps)
x = torch.from_numpy(x_np[np.newaxis, :, np.newaxis]) # shape (batch, time_step, input_size)
y = torch.from_numpy(y_np[np.newaxis, :, np.newaxis])
print("x: ")
print(x)
prediction, h_state = rnn(x, h_state) # rnn output
# !! next step is important !!
h_state = h_state.data # repack the hidden state, break the connection from last iteration
loss = loss_func(prediction, y) # calculate loss
optimizer.zero_grad() # clear gradients for this training step
loss.backward() # backpropagation, compute gradients
optimizer.step() # apply gradients
# # plotting
# plt.plot(steps, y_np.flatten(), 'r-')
# plt.plot(steps, prediction.data.numpy().flatten(), 'b-')
# plt.draw();
# plt.pause(0.05)
# plt.ioff()
# plt.show()