Dive into deep learning(02)[动手学深度学习]———————第二章,线性神经网络
前言:最近在忙毕业论文初稿,自己这方面花的时间也确实少,国庆几天也都是在寝室摆烂,但终归还是要看一点的,马上初稿就要过去了,学校里方面也就没啥事情了,要更努力了呢。
本章摘要:
1、图片数据集准备(image-classification-dataset)
关于MNIST数据集的一些介绍,然后一些图像显示的函数,数据导入的函数。
MNIST数据集是图像分类中广泛使用的数据集之一,但作为基准数据集过于简单。 我们将使用类似但更复杂的Fashion-MNIST数据集。
这里还有部分讲到数据读取,也就是torch里面DataLoader部分,里面的读取参数,batchsize(数据一批的多少)和num_workers(工作线程)都会影响读取快慢,一般读取越快越好,读取要略快于数据处理一趟的速度。
2、线性回归介绍(linear-regression)
主要是关于线性回归在机器学习中的一些介绍,以及线性回归的损失函数使用均方误差的原因,因为在噪点为服从高斯分布的假设下时,最小化均方误差和最大化似然函数是等价的。最大化似然函数在统计中一般用来参数估计,和我们这里的用均方误差损失函数估计模型参数本质是一样的。
机器学习模型中的关键要素是训练数据、损失函数、优化算法,还有模型本身。
矢量化使数学表达上更简洁,同时运行的更快。
最小化目标函数和执行极大似然估计等价。
线性回归模型也是一个简单的神经网络。
作业:
是一些数学推导,有些题目还看的有点迷糊。前两题还好,第三题有点迷糊,有些东西真的越学越觉得不够,数学仍是基础。插个眼,回头有空再看看。
3、线性回归代码从0开始(linear-regression-scratch)
主要分为几步,第一步生成随机数据,第二步对数据随机打乱并抽取,第三步确定模型,即哪些参数需要计算。第四步确定损失函数,第五步确定优化算法,这里需要人为设置超参数,例如学习率。最后一步就是把之前的整合,开始训练。
作业:
作业都挺简单的。
函数记录:
random.shuffle(indices)##这里有一个随机抽样的思路,就是把下标打乱,然后用for循环,整组整组抽取数据。
4、线性回归代码pytorch框架简洁实现(linear-regression-concise)
步骤和3里面一样,不过是调用torch里面的api,更快更方便。
作业:
作业也很简单,就不记录了。
函数记录:
net[0].weight.data.normal_(0, 0.01) ##设置权重参数的初始分布
net[0].bias.data.fill_(0) ##设置偏置的初始值为0
w = net[0].weight.data ##查看权重具体值
5、softmax回归介绍(softmax-regression)
softmax与线性回归的差异在于,softmax适合多分类问题,当涉及多分类问题是,处理方式变为计算每个类别的概率,然后选择概率最大的类别。但深度学习最后显示的输出未必是一个概率,因此我们需要一个函数把输出值映射到0-1的概率上去,因此softmax出现了。其中的损失函数也不再是均方误差,而是改为概率里常用的交叉熵形式。
one-hot编码,算是加深理解了,以前都不明所以,现在了解了一丢,one-hot编码的目的是为了消除数字差异性,同样是三分类问题,标签用1,2,3和(0,0,1)(0,1,0)(1,0,0)相比,后者消除了自然数字间的差异性。
作业:
还是数学方面的推导,插眼
函数记录:
6、softmax回归代码从0开始(softmax-regression-scratch)
好像没什么特别需要注意的,有一个点是计算损失的时候,因为这里的标签类型是多分类问题,所以计算损失的时候,可以使用torch里面的切片来来进行计算损失。
例如:
y = torch.tensor([0, 2])
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
y_hat[[0, 1], y]
作业:
1、在本节中,我们直接实现了基于数学定义softmax运算的softmax函数。这可能会导致什么问题?提示:尝试计算 \exp(50) 的大小。
如果网络参数初始化不恰当,或者输入有数值较大的噪音,基于数学定义的softmax运算可能造成溢出(结果超过long类型的范围)
2、本节中的函数 cross_entropy 是根据交叉熵损失函数的定义实现的。这个实现可能有什么问题?提示:考虑对数的值域。
y_hat中若某行最大的值也接近0的话,loss的值会超过long类型范围。
3、你可以想到什么解决方案来解决上述两个问题?
设定一个阈值,使得loss处于long类型能表达得范围内。
抄了一下别人的作业。
函数记录:
7、softmax回归代码pytorch框架简洁实现(softmax-regression-concise)
这里的重点是上下溢问题
softmax为映射函数,当原本的数值过大时,经过softmax映射之后会出现上溢问题。会使得映射之后的数据变为0,inf甚至nan
解决这个问题是对原数据进行无量纲化,减去最大值作数据平移,但这样有可能会产生下溢问题,即分子有可能为0,从而使得原数据经过softmax之后变为0,可是在之后计算损失的时候,使用的log函数取0的时候会产生无穷小,也就是nan,这也是我们不想得到的。但好在如果直接跳过这个中间步骤,即直接对原数据无量纲化之后,把softmax过程直接加到表达式,之后直接求loss,可以抵消部分exp和ln的影响。具体推导如下:
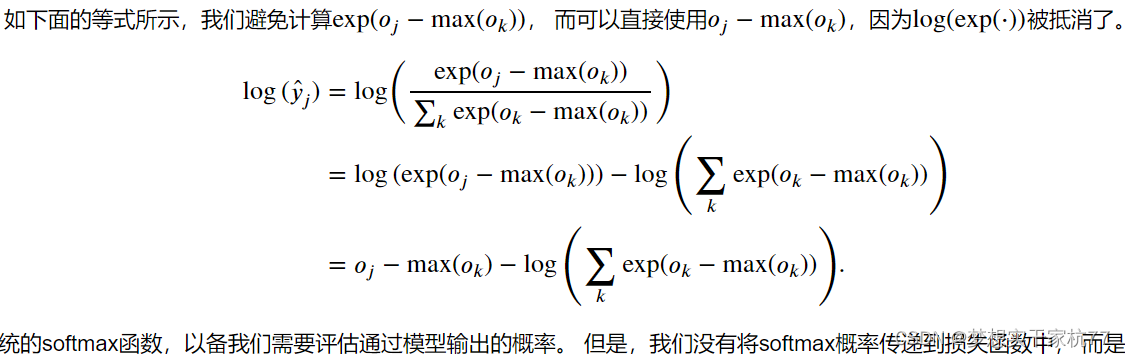
作业:
感觉作业有一点预习的内容,一个模型训练次数过多会发生过拟合。
函数记录: