Deep Residual Learning for Image Recognition
摘要:
背景:神经网络越深越难训练
解决:提出一个残差学习框架
要点:使得各个层根据输入学习残差函数F(x)而不是原始未参考的函数H(x)
结论:使得网络更容易优化,并且网络加深也不会影响准确率
1. Introduction介绍
0.plain网络
可以看到,网络越深,误差越大。
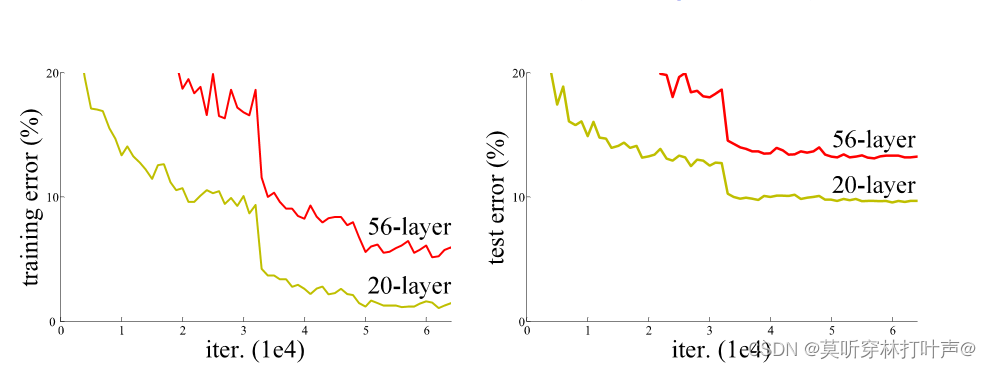
在深度学习的驱使下,一个新的问题产生了:想要训练一个更好的网络,是不是直接堆叠更多的层就行?当然不是。
网络变深了就会有梯度消失/爆炸的问题,阻止了模型的收敛。然而
- 归一初始化normalized initialzation
- 中间归一化intermedizte normalization
很大程度上解决了这一问题。
1.1 退化问题
当更深的网络能够开始收敛时,退化问题就暴露出来了:随着网络深度的增加,准确率会达到饱和(不足为奇),然后准确率迅速退化。但是这种退化不是由过拟合引起的,在一个合适的深度模型中增加更多的层会导致更高的训练误差。
解决方案:改变添加更多层网络的方式
- 增加的层使用恒等映射
得到两个网络,一个是较浅的普通的网络,一个是使用恒等映射的较深网络。
结果:
- 较深的模型误差更小
问题:
- 解算器无法找到与构建的解相当或者更好的解(或无法在可行的时间内找到)
直接学习H(x)比较困难,所以学习F(x)
1.2 梯度消失问题Vanishing Gradient Problem
梯度消失会阻止网络的进一步训练。
eg:sigmoid激活函数的偏导数最大值为0.25。当网络中有很多层时,导致乘积的值会减少,直到某个点损失函数的偏导数接近于0,导致偏导数消失,称之为梯度消失。
两种解决方式:
- 使用其他的激活函数ReLU()
- 构建残差块
1.3 Deep residual learning framework深度残差学习框架
构造深层网络的解决方案:
- 通过恒等映射identity mapping构建增加的层
深层模型不应该产生比浅层模型更高的训练误差。但是SGD找不到这个效果。不能直接学习H(x)。
- 本文中通过引入深度残差学习框架来解决退化问题
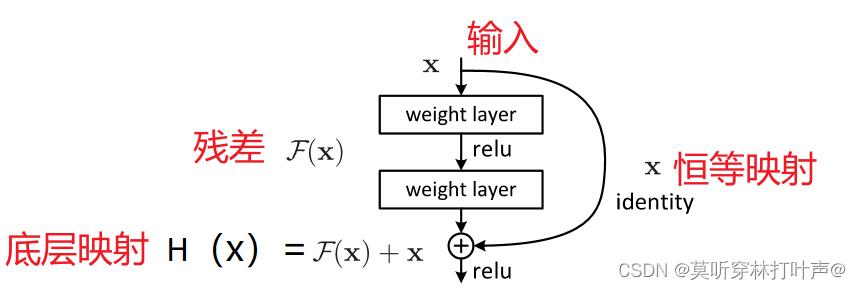
本文让网络层拟合残差映射residual mapping,而不是直接来拟合所需的底层映射desired underlying mapping。拟合F(x),而不是拟合H(x)。
将所需的底层映射表示为H(x),让堆叠的非线性层来拟合另一个映射F(x)=H(x)-x。原始映射被转化成F(x)+x。
我们现在是恒等映射,将x直接恒等映射过来。想要H(x)=x,即要将F(x)推至0。
Residual block把我们需要解决的问题从通过将x映射y(H(x))转变成根据x求x与y(H(x))之间的距离F(x)。所谓反向传播就是网络输出一个值,然后与真实值做比较得到的一个误差损失,同时将这个损失做差改变参数,返回的损失大小取决于原来的损失和梯度,既然目的是改变参数,而问题是改变参数的力度过小,则可以减少参数的值,使损失对参数改变的力度相对增大。
- 残差映射比原始未参考的映射unreferenced mapping更容易优化,我们要将残差推到零
F(x)+x,即为identity mapping,通过前馈神经网络的shortcut connection来实现。shortcut只执行恒等映射,不添加额外的参数和计算复杂度,整个网络仍然可以使用SGD进行计算,无需修改解算器。
152层的残差网络复杂性仍低于VGG网络。
结果:
- 残差网络更易于优化
- 相同深度的plain网络和残差网络相比,残差网络的训练误差更小
- 泛化能力更好
2.Related Work 相关工作
2.1 Residual Representations
残差向量编码比原始向量编码更加有效;
一些方法表明:良好的重构或预处理可以简化优化问题。
2.2 shortcut Connections
多层感知机、Goging、deeply都采用了shortcut Connections,解决了梯度消失/爆炸问题。
我们的公式总是学习残差函数,我们的shortcut Connections从来不关闭,所有的信息总是要通过的。
3.Deep Residual Learning 深度残差学习
3.1 Residual Learning 残差学习
假设输入维度和输出维度相同时,我们学习残差函数F(x)=H(x)-x,而不是学习H(x),因此原始函数变成F(x)+x,但是学习的难易程度不同。
- 学习F(x)=H(x)-x=0更加容易。并且模型不会变差,因为F(x)=0时,输入输出是相等的
- 如果添加的层可以被构造为恒等映射,那么更深的模型的训练误差应该不大于与其对应的浅层网络
3.2 通过shortcuts进行恒等映射

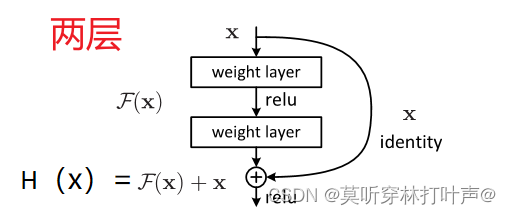
对于上面具有两层的残差块:
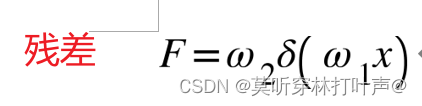
对于维度相同的映射:实线跳跃连接
残差F(x):输入x乘第一层的权重,经过一次非线性激活,再乘第二层的权重。
再将得到的F(x)加恒等映射x后得y,再执行一次非线性激活。

对于维度不同的映射:虚线跳跃连接

这个Ws是用来匹配维度的,并且仅用来匹配维度。通过快捷连结来执行线性投影Ws来匹配维度。

一般残差块是两层或者三层的效果比较好,一层的效果没有优势。
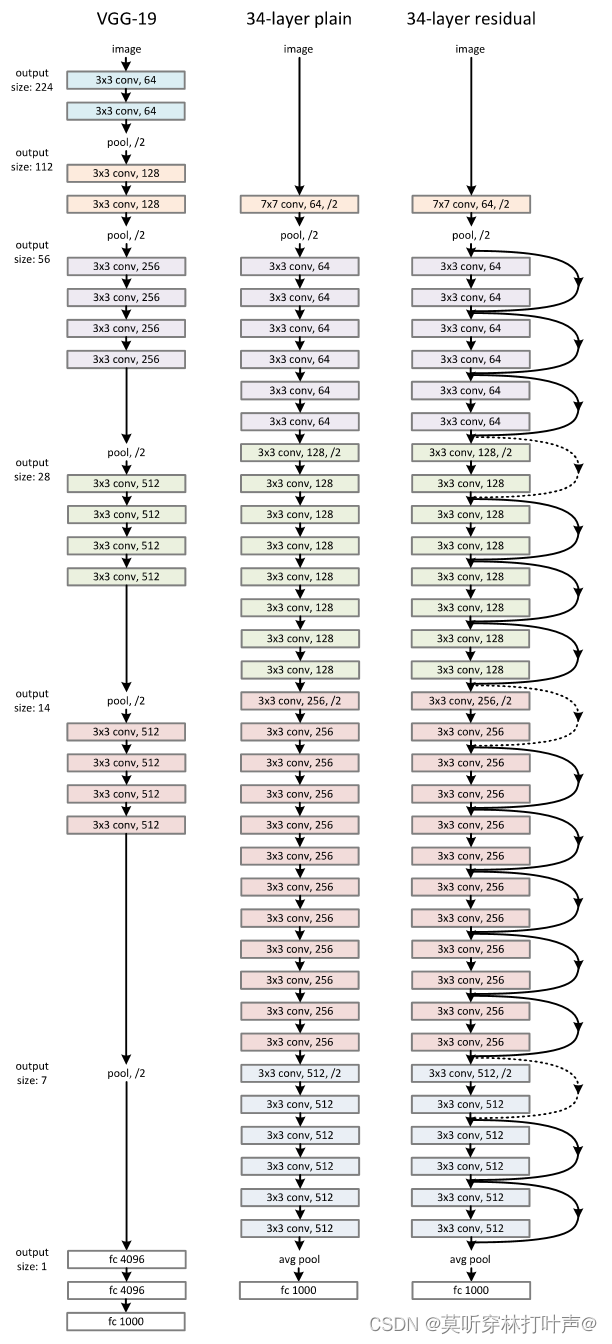
3.3 Network Architectures网络架构
受到VGG网络的启发,采用以下原则:比VGG网有更少的卷积核和更低的复杂性
这里的验证看后续的代码
- 对于相同的特征图大小,各层具有相同数量的l滤波器
- 特征图数量减半,则滤波器数量加一倍(如果通道数/卷积核的数量翻了两倍,输入的高和宽通常都会减半)
- 步长为2的卷积层直接执行下采样(每个残差块的第一个卷积层)
- 网络以一个全局平均池化层和具有1000路全连接层的softmax结束。加权层的总数是34
当输入和输出具有相同的维度的时候:
采用shortcut实现连接方式
当输入和输出具有不同维度的时候:
一般都采用后者。
- 在增加的维度上用0来填充,不会增加额外的参数
- Ws的方式,通过1×1的卷积做映射,stride=2,在空间无作用,主要为了改变通道的维度
具体做法:
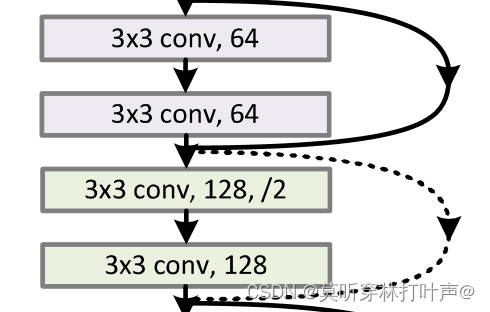
上图中的通道数从64变为128,采用的是步长为2,输出通道为128的1×1卷积来实现。
3.4 Implementation
224×224的图像,使用图像增强;
在卷积之后和激活之前都采用批量归一化(BN);
学习率从0.1开始,误差达到稳定水平的时候/10;
4.Experiments 实验
4.1图像分类
Plain Networks: 34层比18层的误差高。但是不是由于梯度消失引起的,因为采用的BN层(BN层保证了梯度),可能是因为收敛速度太慢,影响了训练误差。
ResNet: 只是增加了恒等映射,使用0填充(无参数),34就比18好。
证明了0填充(无参数)易于训练。再证明1×1卷积的方法比0填充更好,代码几乎使用这一种方法(增加维度的使用1×1的卷积,其余为恒等映射),代码验证在后面。
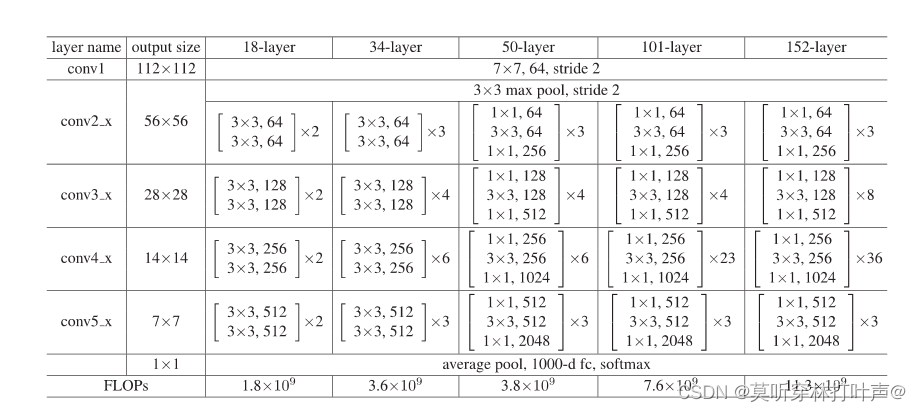
18,34采用两层的残差块,50,101,152采用三层的残差块,称为瓶颈设计bottenech design:
- 1×1 负责减少然后恢复维度
- 3×3具有较小输入/输出维度的瓶颈
4.2 在CIFAR10上的分类
不使用maxout/dropout,采用正则化来防止过拟合
展望: 结合更强的正则化来改善效果
4.3 目标检测
也有改善。
5.代码
下次再写。