[人工智能]填充与步幅(CNN卷积神经网络)

填充和步幅

由之前的学习，可以知道，假设输入形状为 $X_h\times X_w$ ，卷积核形状为 $K_h\times K_w$ ，那么输出形状将是 $(X_h?K_h+1)\times (X_w?K_w+1)$ 。因此，卷积的输出形状取决于输入形状和卷积核的形状。

还有什么因素会影响输出的大小呢？本节我们将介绍 填充（padding） 和 步幅（stride）。

填充(Padding)

在应用多层卷积时，我们常常丢失边缘像素。 由于我们通常使用小卷积核，因此对于任何单个卷积，我们可能只会丢失几个像素。 但随着我们应用许多连续卷积层，累积丢失的像素数就多了。

解决这个问题的简单方法即为填充（padding）：在输入图像的边界填充元素（通常填充元素是 $0$ ）。

例如，在下图中，我们将 $3\times 3$ 输入填充到 $5\times 5$ ，那么它的输出就增加为 $4\times 4$ 。阴影部分是第一个输出元素以及用于输出计算的输入和核张量元素：

$$0\times 0+0\times 1+0\times 2+0\times 3=0$$

通常，如果我们添加 $p_h$ 行填充（大约一半在顶部，一半在底部）和列 $p_w$ 填充（左侧大约一半，右侧一半），则输出形状将为

$$(n_h?k_h+p_h+1)\times (n_w?k_w+p_w+1)$$

这意味着输出的高度和宽度将分别增加 $p_h$ 和 $p_w$ 。

在许多情况下，我们需要设置 $p_h=k_h?1$ 和 $p_w=k_w?1$ ，使输入和输出具有相同的高度和宽度。

此外，使用奇数的核大小和填充大小也提供了书写上的便利。对于任何二维张量X，当满足： 1. 卷积核的大小是奇数； 2. 所有边的填充行数和列数相同； 3. 输出与输入具有相同高度和宽度 则可以得出：输出 $Y[i,j]$ 是通过以输入 $X[i,j]$ 为中心，与卷积核进行互相关计算得到的。

比如，在下面的例子中，我们创建一个高度和宽度为 3 的二维卷积层，并在所有侧边填充 1 个像素。给定高度和宽度为 8 的输入，则输出的高度和宽度也是 8 。

import torch                                   #引入torch包
from torch import nn                           #引入torch中的nn神经网络


#为了方便起见，我们定义了一个计算卷积层的函数
#此函数初始化卷积层权重，并对输入和输出提高和缩减相应的维度
def comp_conv2d(conv2d, X):
    #这里的 (1, 1) 表示批量大小和通道数都是1
    X = X.reshape((1, 1) + X.shape)
    Y = conv2d(X)
    #省略前两个维度: 批量大小和通道
    return Y.reshape(Y.shape[2:])

#请注意，这里每边都填充了1行或1列，因此总共填充了2行和2列
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1)
X = torch.rand(size=(8,8))
comp_conv2d(conv2d, X).shape

torch.Size([8, 8])

当卷积核的高度和宽度不同时，我们可以填充不同的高度和宽度，使输出和输入具有相同的高度和宽度。在如下示例中，我们使用高度为5，宽度为3的卷积核，高度和宽度两边的填充分别为2和1。

conv2d = nn.Conv2d(1, 1, kernel_size=(5, 3), padding=(2, 1))
comp_conv2d(conv2d, X).shape

torch.Size([8, 8])

步幅(Stride)

在计算互相关时，卷积窗口从输入张量的左上角开始，向下、向右滑动。 在前面的例子中，我们默认每次滑动一个元素。 但是，有时候为了高效计算或是缩减采样次数，卷积窗口可以跳过中间位置，每次滑动多个元素。

我们将每次滑动元素的数量称为 步幅（stride） 。

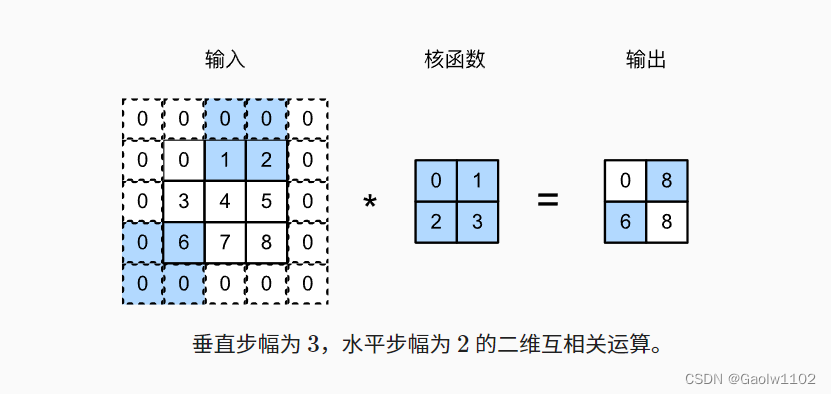
下图是垂直步幅为 $3$ ，水平步幅为 $2$ 的二维互相关运算。 着色部分是输出元素以及用于输出计算的输入和内核张量元素：

$$\begin{gathered} 0\times 0+0\times 1+1\times 2+2\times 3=8 \\ 0\times 0+6\times 1+0\times 2+0\times 3=6 \end{gathered}$$

通常，当垂直步幅为 $s_h$ 、水平步幅为 $s_w$ 时，输出形状为

$$?(n_h?k_h+p_h+s_h)/s_h?\times ?(n_w?k_w+p_w+s_w)/s_w?$$

如果我们设置了 $p_h=k_h?1$ 和 $p_w=k_w?1$，则输出形状将简化为

$$?(n_h+s_h?1)/s_h?\times ?(n_w+s_w?1)/s_w?$$

更进一步，如果输入的高度和宽度可以被垂直和水平步幅整除，则输出形状将为

$$(n_h/s_h)\times (n_w/s_w)$$

下面，我们将高度和宽度的步幅设置为2，从而将输入的高度和宽度减半。

#定义卷积核，输入输出管道分别为1、1，卷积核为(3,3)，行列均填充2，步数为2
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1, stride=2)
comp_conv2d(conv2d, X).shape

torch.Size([4, 4])

接下来，看一个稍微复杂的例子。

conv2d = nn.Conv2d(1, 1, kernel_size=(3, 5), padding=(0, 1), stride=(3, 4))
comp_conv2d(conv2d, X).shape

torch.Size([2, 2])

在实践中，我们很少使用不一致的步幅或填充，也就是说，我们通常有 $p_h=p_w$ 和 $s_h=s_w$ 。

小结

1. 填充可以增加输出的高度和宽度。这常用来使输出与输入具有相同的高和宽。

2. 步幅可以减小输出的高和宽，例如输出的高和宽仅为输入的高和宽的 $1/n$（ $n$ 是一个大于的整数）。

3. 填充和步幅可用于有效地调整数据的维度。