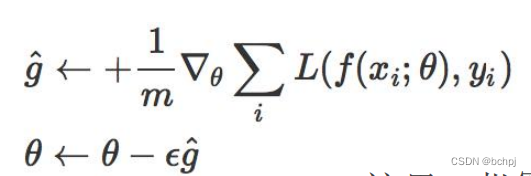神经网络
模拟了大脑的结构,利用大量神经元按照一定的体系架构连接成网状的结构。简单地讲就是通过神经网络在输入和输出之间建立联系。
人工神经元
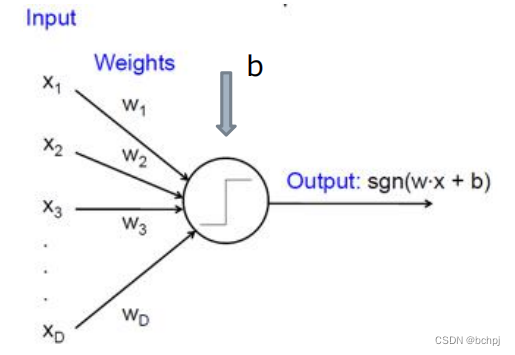
接受前一层传来的数据,并将这些数据的加权和输入非线性作用函数中,最后将非线性作用函数的输出结果传递给后一层。
输入向量
x
x
x
权重向量
w
w
w偏置标量
b
b
b
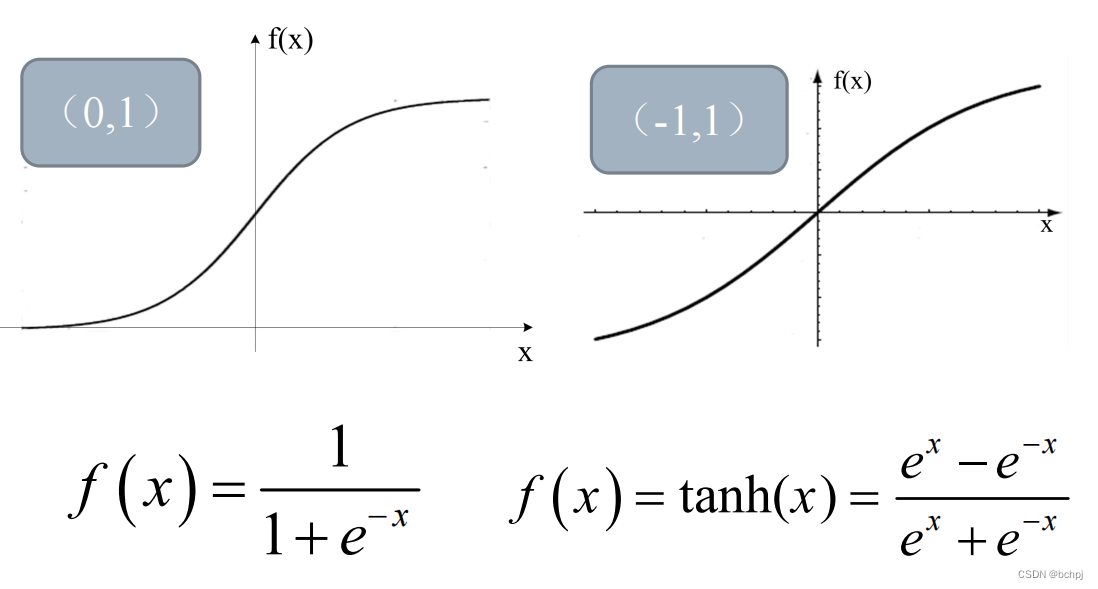
激活函数
s
i
g
m
o
i
d
sigmoid
sigmoid
激活函数
y
=
f
(
w
t
x
)
=
f
(
∑
i
=
1
d
w
i
x
i
)
y = f(w^{t}x)=f(\sum_{i=1}^dw_{i}x_{i})
y=f(wtx)=f(i=1∑d?wi?xi?)
非线性函数
f
f
f,称为激活函数。
前馈神经网络
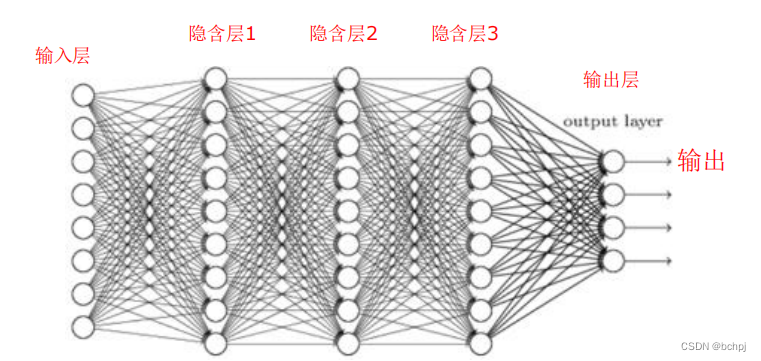
1、前馈神经网络,是人工神经网络的一种,各神经元从输入层开始,接收前一级输入,并输出到下一级,直至输出层。整个网络中无反馈,可用一个有向无环图表示。
2、前馈神经网络采用一种单向多层结构。其中每一层包含若干个神经元,同一层的神经元之间没有互相连接,层间信息的传送只沿一个方向进行。
3、其中第一层称为输入层。最后一层为输出层.中间为隐含层。隐含层可以是一层,也可以是多层。
目标函数
J
(
w
)
=
1
2
∣
∣
t
?
z
∣
∣
2
=
1
2
∑
k
=
1
c
(
t
k
?
z
k
)
2
J(w)=\frac{1}{2}||t-z||^{2}=\frac{1}{2}\sum_{k=1}^{c}(t_{k}-z_{k})^{2}
J(w)=21?∣∣t?z∣∣2=21?k=1∑c?(tk??zk?)2
对于一系列训练样本x,期望的输出是
t
=
(
t
1
,
t
2
,
,
,
t
c
)
t=(t_{1},t_{2},,,t_{c})
t=(t1?,t2?,,,tc?),网络的实际输出是
z
=
(
z
1
,
z
2
,
,
,
z
c
)
z=(z_{1},z_{2},,,z_{c})
z=(z1?,z2?,,,zc?)。共有c个样本。
梯度的反向传播
举例计算:
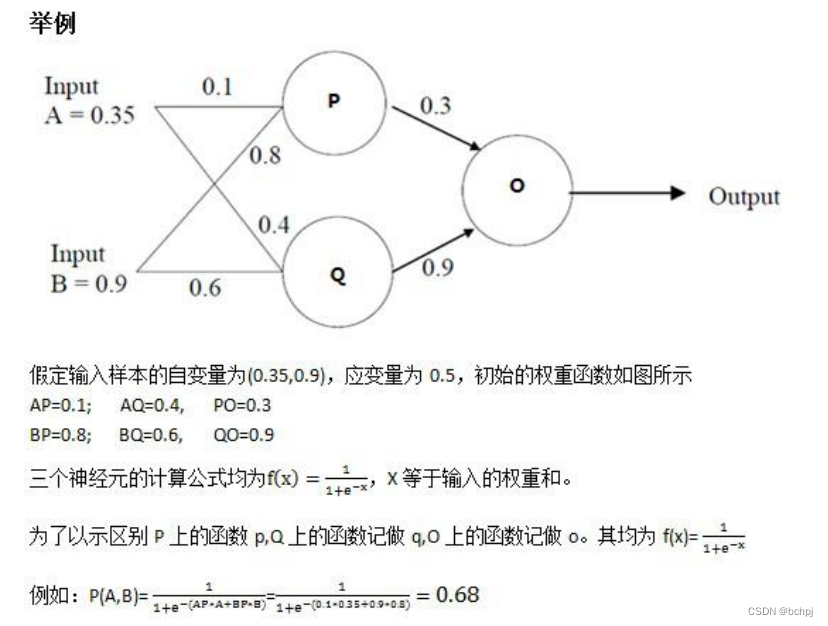

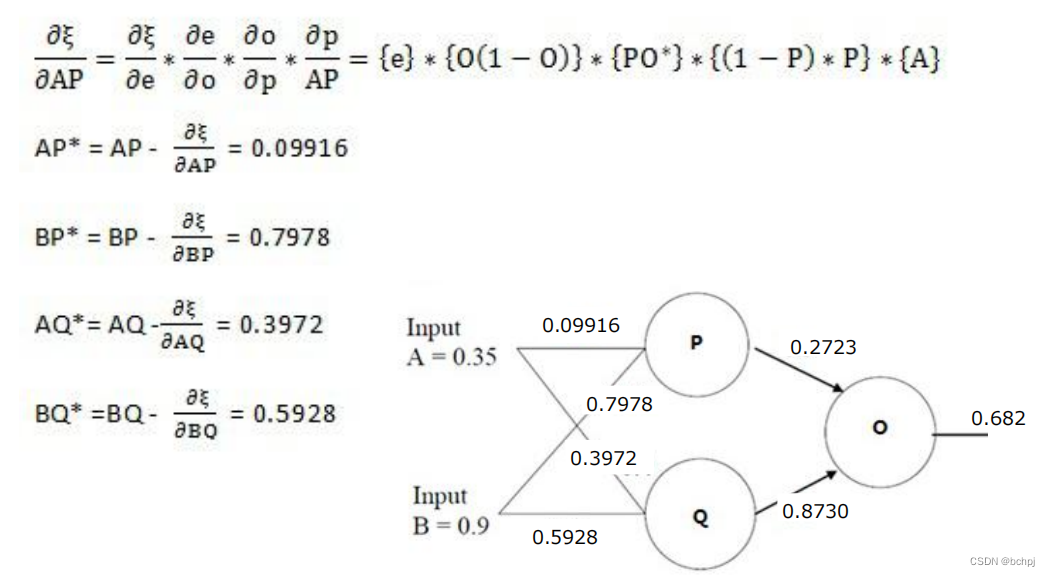
梯度下降的方法
批量梯度下降:每迭代一步,都要用到训练集所有的数据,它得到的是一个全局最优解,但是如果m很大,那么可想而知这种方法的迭代速度!!
随机梯度下降(SGD):通过每个样本来迭代更新一次,如果样本量很大的情况,那么可能只用其中部分的样本,就已经迭代到最优解了。但是,SGD伴随的一个问题是噪音较BGD要多,使得SGD并不是每次迭代都向着整体最优化方向。
Mini-batch Gradient Descent:mini-batch Gradient Descent的方法是在”批量梯度下降”和*随机梯度下降”两种方法中取折衷,每次从所有训练数据中取一个子集(mini-batch)用于计算梯度。广义条件下,SGD指的就是MBGD。