[人工智能]深度学习：Diffusion Models in Vision: A Survey视觉中的扩散模型:综述

论文下载

0.摘要

去噪扩散模型是计算机视觉领域的一个新兴课题，在生成建模领域取得了显著的成果。扩散模型是一种基于正向扩散和反向扩散两个阶段的深层生成模型。在正向扩散阶段，通过添加高斯噪声对输入数据进行逐步扰动。在反向阶段，模型的任务是通过学习逐步反向扩散过程来恢复原始输入数据。扩散模型因其生成的样本的质量和多样性而受到广泛赞赏，尽管它们已知的计算负担，如。由于采样过程中涉及的步骤较多，导致速度较低。在这个综述中，我们提供了在视觉中应用去噪扩散模型的文章的综合综述，包括在该领域的理论和实践贡献。首先，我们确定并提出了三种通用的扩散建模框架，它们基于去噪扩散概率模型、噪声条件评分网络和随机微分方程。我们进一步讨论了扩散模型和其他深层生成模型之间的关系，包括变分自编码器、生成对抗网络、基于能量的模型、自回归模型和归一化流。然后，介绍了计算机视觉中扩散模型的多视角分类。最后，我们说明了目前扩散模型的局限性，并展望了未来研究的一些有趣的方向

1.概述

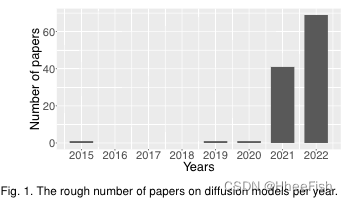
Diffusion Models [1] -[11]形成了一类深度生成模型，它最近成为计算机视觉领域最热门的话题之一，展示了令人印象深刻的生成能力，从高水平的细节到生成示例的多样性。我们甚至可以说，这些生成模型将生成建模领域的门槛提高到了一个新的水平，特别是参考了诸如Imagen[12]和潜扩散模型(LDM)[10]等模型。迄今为止，扩散模型已应用于各种生成建模任务，如图像生成[1]-[7]，[10]-[22]，图像超分辨率[10]，[12]，[23]-[26]，图像绘制[1]，[3]，[4]，[10]，[23]，[25]，[27]-[29]，图像编辑[30]-[32]，图像间翻译[31]，[33]-[37]等。此外，通过扩散模型学习到的潜在表征也被发现在辨别任务中是有用的。图像分割[38]-[41]，分类[42]，异常检测[43]-[45]。这证实了去噪扩散模型的广泛适用性，表明进一步的应用还有待发现。此外，学习强潜在表征的能力与表征学习[46]，[47]建立了联系，[47]是一个综合领域，研究学习强大数据表征的方法，涵盖多种方法，从设计新颖的神经结构[48]-[51]到发展学习策略[52]-[57]。
根据图1所示的图表，扩散模型的论文数量正以非常快的速度增长。为了概述这一快速发展的主题的过去和目前的成就，我们提出了一个全面的回顾文章去噪扩散模型在计算机视觉。更准确地说，我们调查了属于以下定义的生成模型类别的文章。扩散模型代表一类深度生成模型，它们基于(i)正向扩散阶段，在这个阶段中，输入数据通过添加高斯噪声在几个步骤中逐渐被扰动;(ii)反向(向后)扩散阶段，在这个阶段中，生成模型的任务是从扩散(噪声)数据中逐步学习反向扩散过程，以恢复原始输入数据。
我们强调，至少有三个子类别的扩散模型符合上述定义。第一类包括去噪扩散概率模型(DDPMs)[1]，[2]，这是受非平衡热力学理论的启发。DDPMs是一种潜在变量模型，它使用潜在变量来估计概率分布。从这个角度来看，DDPMs可以被看作是一种特殊的变分自动编码器(VAEs)[49]，其中正向扩散阶段对应于VAE内部的编码过程，而反向扩散阶段对应于解码过程。第二个子类别由噪声条件评分网络(NCSNs)[3]表示，它基于通过评分匹配训练共享神经网络来估计不同噪声水平下受扰数据分布的评分函数(定义为日志密度的梯度)。随机微分方程(SDEs)[4]代表了一种模拟扩散的替代方法，形成了扩散模型的第三个子类别。通过正向和反向SDEs建模扩散可以得到有效的生成策略和强有力的理论结果[58]。后一种提法(基于SDEs)可被视为对DDPMs和NCSNs的一般化。
我们确定了几个定义设计选择，并将它们合成为三个通用扩散建模框架，以响应上述三个子类别。为了将一般的扩散建模框架置于上下文环境中，我们进一步讨论了扩散模型与其他深层生成模型之间的关系。更具体地说，我们描述了它们与变分自编码器(vais)[49]、生成对抗网络(GANs)[51]、基于能量的模型(ems)[59]、[60]、自回归模型[61]和归一化流[62]、[63]的关系。然后，我们介绍了应用于计算机视觉的扩散模型的多视角分类，基于基础框架、目标任务或去噪条件等标准对现有模型进行分类。最后，我们说明了目前扩散模型的局限性，并展望了未来研究的一些有趣的方向。例如，最成问题的限制之一可能是推理过程中较差的时间效率，这是由非常多的评估步骤造成的。数千，生成一个样本[2]。当然，在不影响生成样本质量的前提下克服这一限制是未来研究的一个重要方向。
总之，我们的贡献是总结为以下两个方面：

• 由于最近在视觉中出现了许多基于扩散模型的贡献，我们提供了一个全面和及时的文献综述，用于计算机视觉降噪扩散模型的应用，旨在为我们的读者提供一个通用扩散建模框架的快速理解。
• 我们设计了扩散模型的多视角分类，旨在帮助其他研究扩散模型应用于特定领域的研究人员快速找到相应领域的相关工作

2.通用模型架构

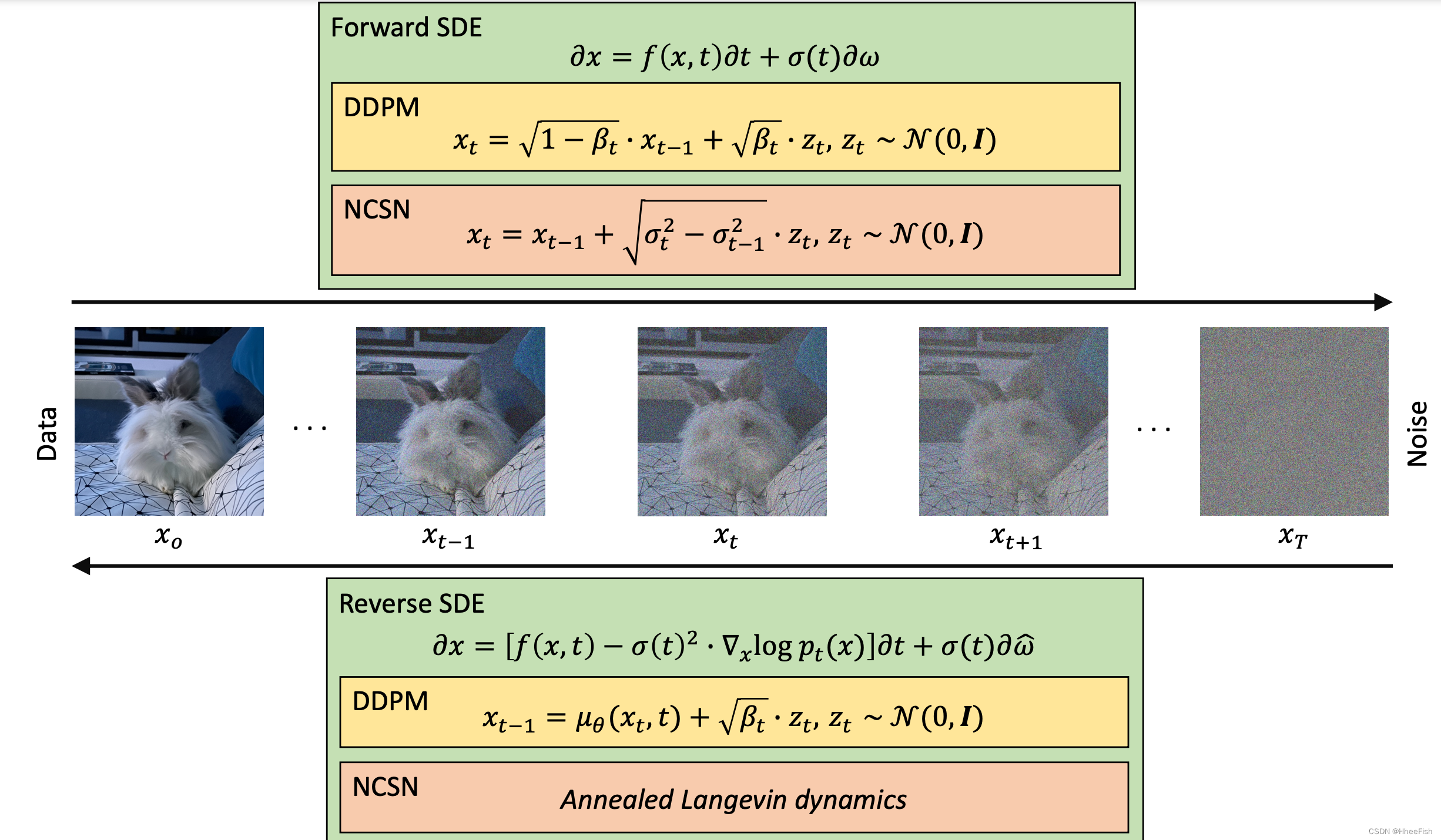
图2所示。一个通用框架，由三种可选扩散模型公式组成:去噪扩散概率模型(DDPMs)、噪声条件评分网络(NCSNs)和随机微分方程(SDEs)。基于SDEs的方程是对其他两种配方的推广。在正向过程中，高斯噪声逐渐添加到输入中。在反向过程中，模型学会通过逐渐去除噪声来恢复原始输入。在SDE公式中，正向过程基于Eq.(11)，反向过程基于Eq.(12)。在DDPM版本中，正向阶段基于Eq.(1)，反向阶段使用Eq.(5)。类似地，在NCSN版本中，正向过程由式(9)推导而来，而反向过程则使用退火的Langevin dynamics。

扩散模型是一类概率生成模型，它可以通过添加不同尺度的噪声来学习反向逐步退化训练数据结构的过程。在接下来的三个小节中，我们提出了三种扩散模型的公式，即去噪扩散概率模型、噪声条件评分网络和基于随机微分方程的方法，这是对前两个方法的概括。对于每个公式，我们描述了向数据添加噪声的过程，学习反转这个过程的方法，以及在推理时如何生成新的样本。在图2中，所有三个公式都作为一个通用框架加以说明。我们将在最后一小节讨论与其他深层生成模型的连接

2.1.Denoising Diffusion Probabilistic Models 去噪扩散概率模型(DDPMs)

DDPMs[1]，[2]使用高斯噪声慢慢破坏训练数据。设$p(x_0)$为数据密度，其中索引0表示数据未损坏(原始)的数据。给定一个未损坏的训练样本$x_{0}p(x_0)$，有噪声的版本$x_1,x_2\dots ，x_T$根据以下马尔可夫过程得到:
p ( x t ∣ x t ? 1 ) = N ( x t ; 1 ? β t ? x t ? 1 , β t ? I ) , ? t ∈ { 1 , . . . . . , T } ，（ 1 ） p(x_t|x_{t-1})=N(x_t;\sqrt{1-\beta_t}·x_{t-1},\beta_t·I),\forall t\in\{1,.....,T\}，（1） p(xt?∣xt?1?)=N(xt?;1?βt? ??xt?1?,βt??I),?t∈{1,.....,T}，（1）
其中，β₁，…，β_T∈[0,1)是表示扩散步骤方差表的超参数，$I$是与输入$x_0$具有相同维数的单位矩阵，$N(x;\mu ,\sigma )$表示满足具有均值μ和方差σ的正态分布的x。这个递归公式的一个重要性质是，当从均匀分布中提取x_t时，它还允许对x_t进行直接采样，即t～U({1，…，T}):
$$p(x_t|x_0)=N(x_t;\sqrt{\hat{\beta }}?x_0,(1?\widehat{{\beta }_t})?I)?$$$$x_t=\sqrt{\hat{\beta }}?x_0+z_t?\sqrt{1?\hat{\beta }}，（2）$$
其中，$z_t\backsim N(0,I),{\alpha }_t=1?{\beta }_t,\hat{\beta }={\prod }_{i=1}^t{\alpha }_i$
在应用Eq. (1)在T轮次中表示的递归过程后，如果添加到数据中的总噪声足够大，则分布$p(x_T)$应该很好地近似于标准高斯分布$\pi (x_T)=N(0,I)$。因此，如果我们从采样$x_{T}N(0,I)$开始，并遵循反向步骤$p(x_{t?1}|x_t)$，我们可以从$p(x_0)$生成新的样本。我们可以训练神经网络$p_{\theta }(x_{t?1}|x_t)$来近似这些步骤。此外,Sohl-Dickstein等人[1]观察到当β足够小时，神经网络$p(x_{t?1}|x_t)$可以被认为是高斯分布，这意味着神经网络$p_{\theta }(x_{t?1}|x_t)$只能估计均值${\mu }_{\theta }(x_t,t)$和协方差${\sum }_{\theta }(x_t,t)$。
训练神经网络的目标是分配给数据的密度的变分下界(variational lower-bound )使用模型$p_{\theta }(x_0)$:
$$L_{vlb}=?log{p}_{\theta }(x_0|x_1)+KL(p(x_T|x_0)||\pi (x_T))+\sum _{t>1}KL(p(x_{t?1}|x_t,x_0)||p_{\theta }(x_{t?1}|x_t))，（3）$$
其中KL表示两个概率分布之间的Kullback-Leibler散度
我们在下面介绍了[2]中采用的另一个目标，它似乎可以提高生成样本的质量。本质上，这个目标训练一个神经网络来估计根据公式（2）绘制的任意示例中的噪声，如下所示：
$$L_{simple}=E_{t～[1,T]}{E}_{x_0～N(0,I)}||z_t?z_{\theta }(x_t,t)|{|}^2，（4）$$
其中，E为期望值，$z_{\theta }(x_t,t)$为预测$x_t$中噪声的网络。在后一种情况下，Hoet al.[2]提出将协方差${\sum }_{\theta }(x_t,t)$固定为常值，并将均值${\mu }_{\theta }(x_t,t)$重写为噪声的函数，如下所示:
$${\mu }_{\theta }=\frac{1}{\sqrt{{\alpha }_t}}?(x_t?\frac{1?{\alpha }_t}{\sqrt{1?{\hat{\beta }}_t}}?z_{\theta }(x_t,t))，（5）$$

2.2.Noise Conditioned Score Networks噪音条件评分网络(NCSNs)

某些数据密度的评分函数p(x)定义为对数密度相对于输入的梯度${?}_{x}logp(x)$。Langevin dynamics方法在p(x)中生成样本时需要这个评分函数，如下所示:
$$x_i=x_{i?1}+\frac{\gamma }{2}{?}_{x}logp(x)+\sqrt{\gamma }?{\omega }_i，（6）$$
其中 i ∈ { 1 , , . . . . , N } , ω i ～ N ( 0 , I ) i\in\{1,,....,N\},\omega_i～N(0,I) i∈{1,,....,N},ωi?～N(0,I),$\gamma$控制分数方向上的更新幅度，x₀从先验分布中采样，该方法递归应用于N→∞步。因此，生成模型在神经网络$s_{\theta }(x)\approx {?}_{x}logp(x)$估计分数后，可以使用上述方法从p(x)采样。这个网络可以通过分数匹配来训练，这种方法需要对以下目标进行优化
$$L_{sm}=E_{x～p(x)}||s_{\theta }(x)?{?}_{x}logp(x)|{|}_2^2，（7）$$
在实践中，不可能直接最小化这一目标，因为${?}_{x}logp(x)$是未知的。然而，还有其他方法可以克服这个问题，如去噪评分匹配[64]和切片评分匹配[65]。
尽管所描述的方法可以用于数据生成，但Song[3]在将此方法应用于实际数据时强调了几个问题。大多数问题都与这多种假设有关。例如，当数据位于低维流形上时，θ(x)的评分估计是不一致的，除了其他影响外，这可能导致Langevin dynamics 永远不会收敛到高密度区域。在同样的工作[3]中，作者证明了这些问题可以通过在不同尺度上用高斯噪声扰动数据来解决。此外，他们提议通过一个单噪声条件评分网络(NCSN)来学习对由此产生的噪声分布的评分估计。
在抽样方面，他们采用了Eq(6)策略。并使用与每个噪声尺度相关的评分估计。形式上，给定一个高斯噪声尺度序列${\sigma }_1<{\sigma }_2<...<{\sigma }_T$，使$p_{{\sigma }_1}(x)\approx p(x_0)$和$p_{{\sigma }_T}(x)\approx N(0,I)$，我们可以训练一个NCSN $s_{\theta }(x,{\sigma }_t)$与去噪分数匹配，使$s_{\theta }(x,{\sigma }_t)\approx {?}_{x}log(p_{{\sigma }_t}(x))$，?t∈{1，…，t}。${?}_{x}log(p_{{\sigma }_t}(x))$可以推导为:
$${?}_{x_t}log{p}_{{\sigma }_t}(x_t|x)=?\frac{x_t?x}{{\sigma }_t}，（8）$$
前提是：$$p_{{\sigma }_t}(x_t|x)=n(x_t;x,{\sigma }_t^2?I)=\frac{1}{{\sigma }_t?\sqrt{2\pi }}?exp(?\frac{1}{2}?(\frac{x_t?x}{{\sigma }_t}{)}^2)，（9）$$
其中$x_t$是x的有噪声版本，exp是指数函数，因此根据Eq7，对所有的$({\sigma }_t{)}_{t=1}^T$使用Eq7，并将梯度替换为Eq.(8)中的形式，通过最小化以下目标训练$s_{\theta }(x_t，{\sigma }_t)$，?t∈{1，…，t}:
$$L_{dsm}=\frac{1}{T}\sum _{t=1}^T\lambda ({\sigma }_t)E_{p(x)}{E}_{x_t～p_{{\sigma }_t}(x_t|x)}||s_{\theta }(x_t,{\sigma }_t)+\frac{x_t?x}{{\sigma }_t}|{|}_2^2，（10）$$
其中$\lambda ({\sigma }_t)$是权重函数
在推理时，通过退火Langevin dynamics算法进行采样。从本质上讲，Eq(6)是适应的，它为每个尺度使用不同的γ值，同时将输出从一个尺度转移到下一个尺度。

2.3.Stochastic Differential Equations随机微分方程(SDEs)

与前两种方法类似，[4]中提出的方法逐渐将数据分布$p(x_0)$转换为噪声。然而，它推广了前两种方法，因为在这种情况下，扩散过程被认为是连续的，从而成为一个随机微分方程(SDE)的解。如[66]所示，这种扩散的反向过程可以用反向时间SDE来建模，该SDE需要每个时间步的密度评分函数。因此，song.[4]的生成模型使用神经网络来估计评分函数，并通过使用数值SDE求解器从$p(x_0)$中生成样本。
正向扩散过程$(x_t{)}_{t=0}^T,t\in [0,t]$的SDE有如下形式:
$$\frac{?x}{?t}=f(x,t)+\sigma (t){\omega }_t??x=f(x,t)??t+\sigma (t)??\omega ，（11）$$
其中$\omega$市高斯噪声，f是偏移系数，$\sigma$是扩散系数，相关的逆时相SDE定义如下：
$$?x=[f(x,t)?\sigma (t{)}^2?{?}_{x}log{p}_t(x)]?t+\sigma (t)?\hat{\omega }，（12）$$
其中$\hat{\omega }$表示当时间从T倒转到0时的 Brownian motion 。
我们可以对神经网络$s_{\theta }(x,t)\approx {?}_{x}log{p}_t(x)$进行训练，优化的目标与Eq.(10)相同，但适用于连续情况，如下:
$$L_{dsn}^{?}=E_t[\lambda (t)E_{p(x(0))}{E}_{p_t(x(t)|x(0))}||s_{\theta }(x,t)?{?}_{x}log{p}_x(x_t|x_0)|{|}_2^2]，（13）$$
其中λ为加权函数，$tU([0,T])$。我们强调，当漂移系数为仿射时，$p_t(x_t|x_0)$为高斯分布。当f不符合这个属性时，我们可以退回到评分匹配[65]。
这种方法的采样可以用公式(12)中SDE上应用的任何数值方法执行。值得注意的是，在[4]中，作者引入了Predictor-Corrector sampler，它可以生成更好的示例。该算法首先使用一种数值方法从当时的SDE中采样，然后使用一种基于分数的方法作为校正器，例如在前一小节中描述的退火朗日万动力学。此外,Song[4]表明常微分方程(ODE)也可以用来模拟反向过程。因此，由SDE解释解锁的另一种采样策略是基于应用于ode的数值方法。后一种策略的主要优点是它的效率。

2.4.与其他生成模型的关系

下面我们将讨论扩散模型和其他类型生成模型之间的联系。我们从基于可能性的方法开始，以生成式副词网络结束。
扩散模型与VAEs[49]有更多的共同点。例如，在这两种情况下，数据被映射到潜在空间，生成过程学习将潜在表示转换为数据。此外，在这两种情况下，都可以将目标函数导出为数据似然的下限，如式(3)所示。然而，两种方法之间存在本质差异，我们将进一步提及其中一些。隐图像的潜在表示包含原始图像的压缩信息，而扩散模型在前进过程的最后一步之后将数据完全销毁。扩散模型的潜在表现与原始数据具有相同的维数，而降低维数则使VAEs工作得更好。最终，映射到隐空间是可训练的，这对于扩散模型的正向过程是不成立的。上述的异同可以成为两种方法未来发展的关键。例如，已有一些工作将其应用于aVAE[17]、[18]的潜在空间，以建立更有效的扩散模型。
自回归模型[61]，[67]将图像表示为像素序列。他们的生成过程通过一个像素一个像素地生成一个图像，以先前生成的像素为条件生成新的样本。这种方法隐含着单向偏差，这明显代表了这类生成模型的局限性。Esser[27]认为扩散模型和自回归模型是互补的，并解决了上述问题。他们的方法学会了通过马尔可夫链来逆转多扩散过程，其中每个过渡都被实现为一个自回归模型。提供给自回归模型的全局信息是由马尔科夫链的上一步给出的。
与扩散模型类似，归一化流[62][63]将数据分布映射为高斯噪声。然而，这两种方法之间的相似性到此为止，因为规范化流程通过学习可逆可微函数以确定性的方式执行映射。与扩散模型相比，这些特性意味着对网络架构的附加约束和可学习的正向过程。连接这两种生成算法的方法是DiffFlow。DiffFlow扩展了扩散模型和归一化流，使反向和正向过程既可训练又随机。
基于能量的模型(ems)[59]，[60]，[69]，[70]侧重于提供密度函数的非归一化版本的估计，称为能量函数。用于训练这类模型的一种流行策略是分数匹配[69]，[70]。在抽样方面，有基于分数函数的马尔可夫链蒙特卡罗(MCMC)方法。因此，扩散模型第2.2小节的公式可以被认为是基于能量的框架的一种特殊情况，确切地说，进行训练和采样只需要需要score函数
在扩散模型[5]兴起之前，就生成样品的质量而言，GANs[51]被许多人认为是最先进的生成模型。由于反目标的存在，GAN也被认为是难以训练的[71]，并且经常遭受模式崩溃。相比之下，扩散模型具有稳定的训练过程，并提供更多的多样性，因为它们是基于似然的。尽管有这些优点，与GANs相比，扩散模型仍然效率不高，需要在推理过程中进行多网络评估。

3.扩散模型的分类

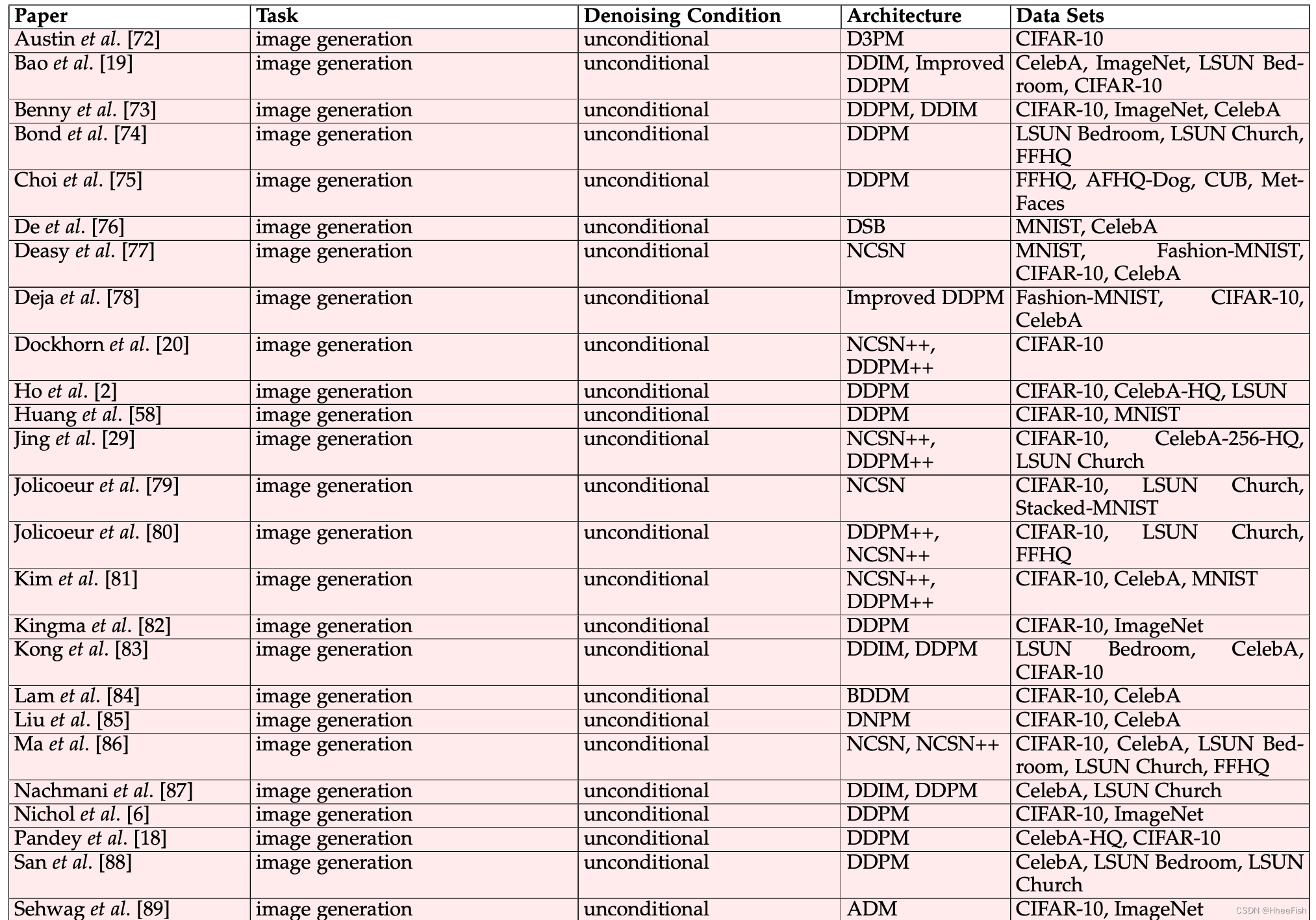
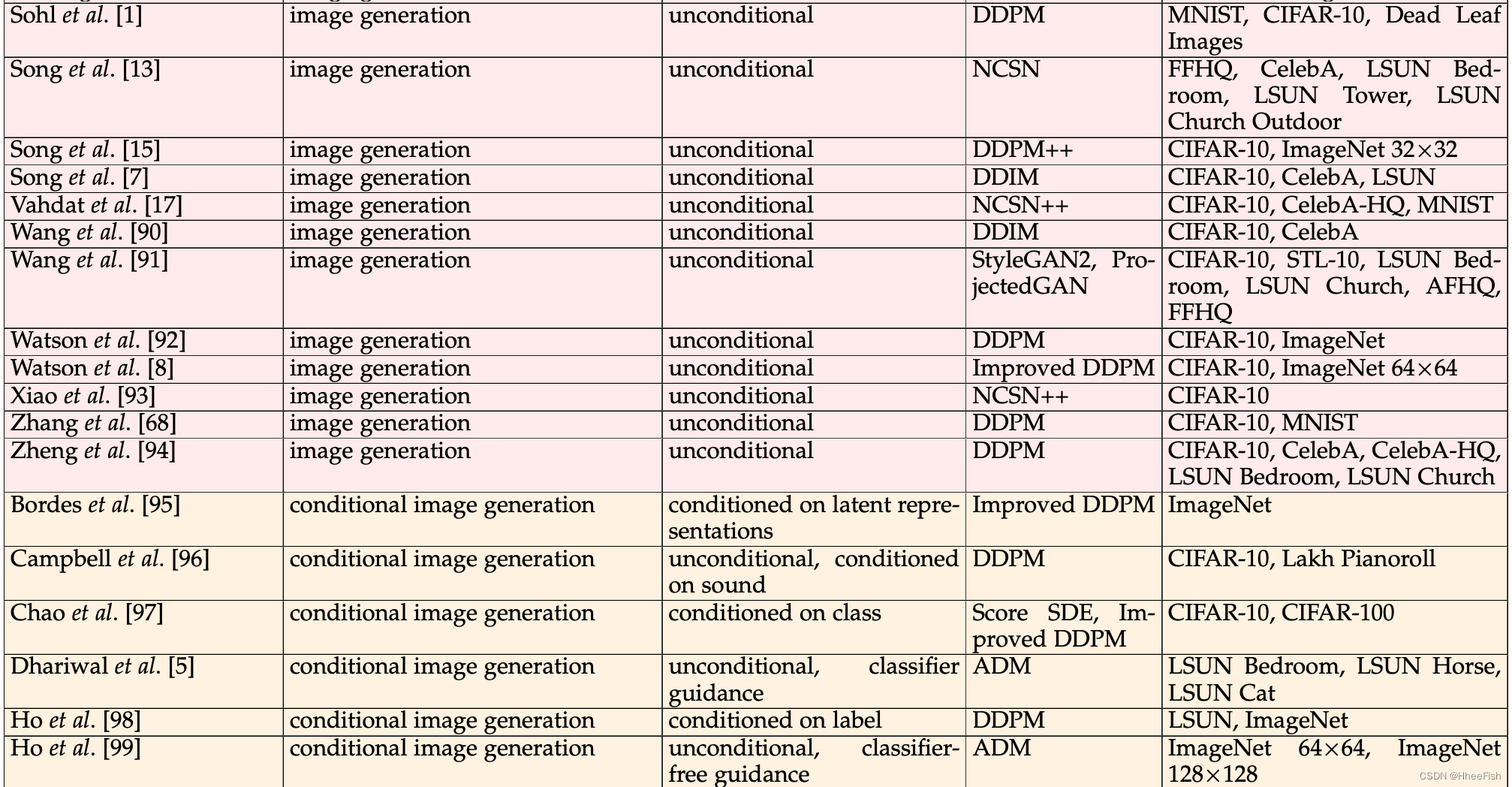
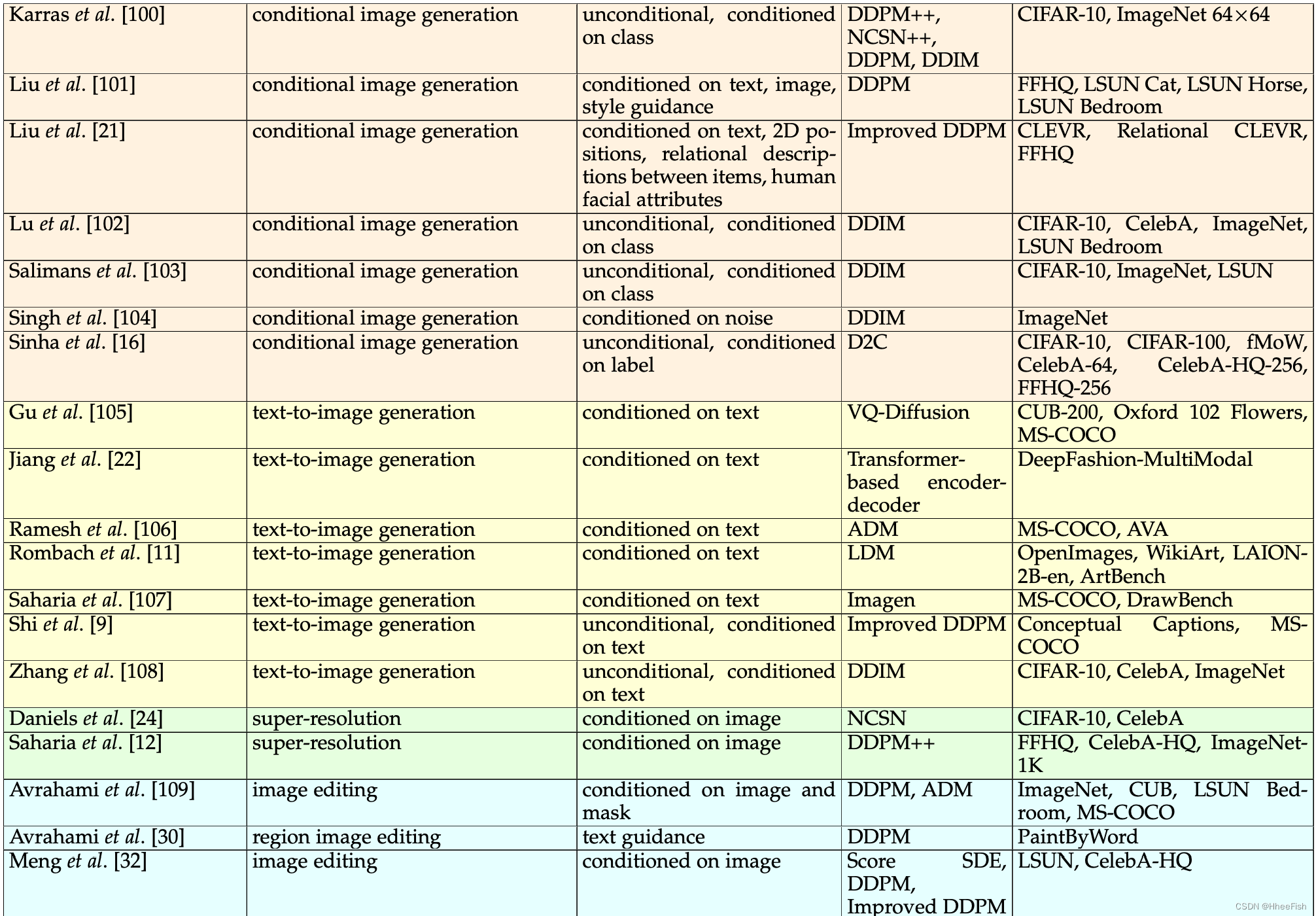
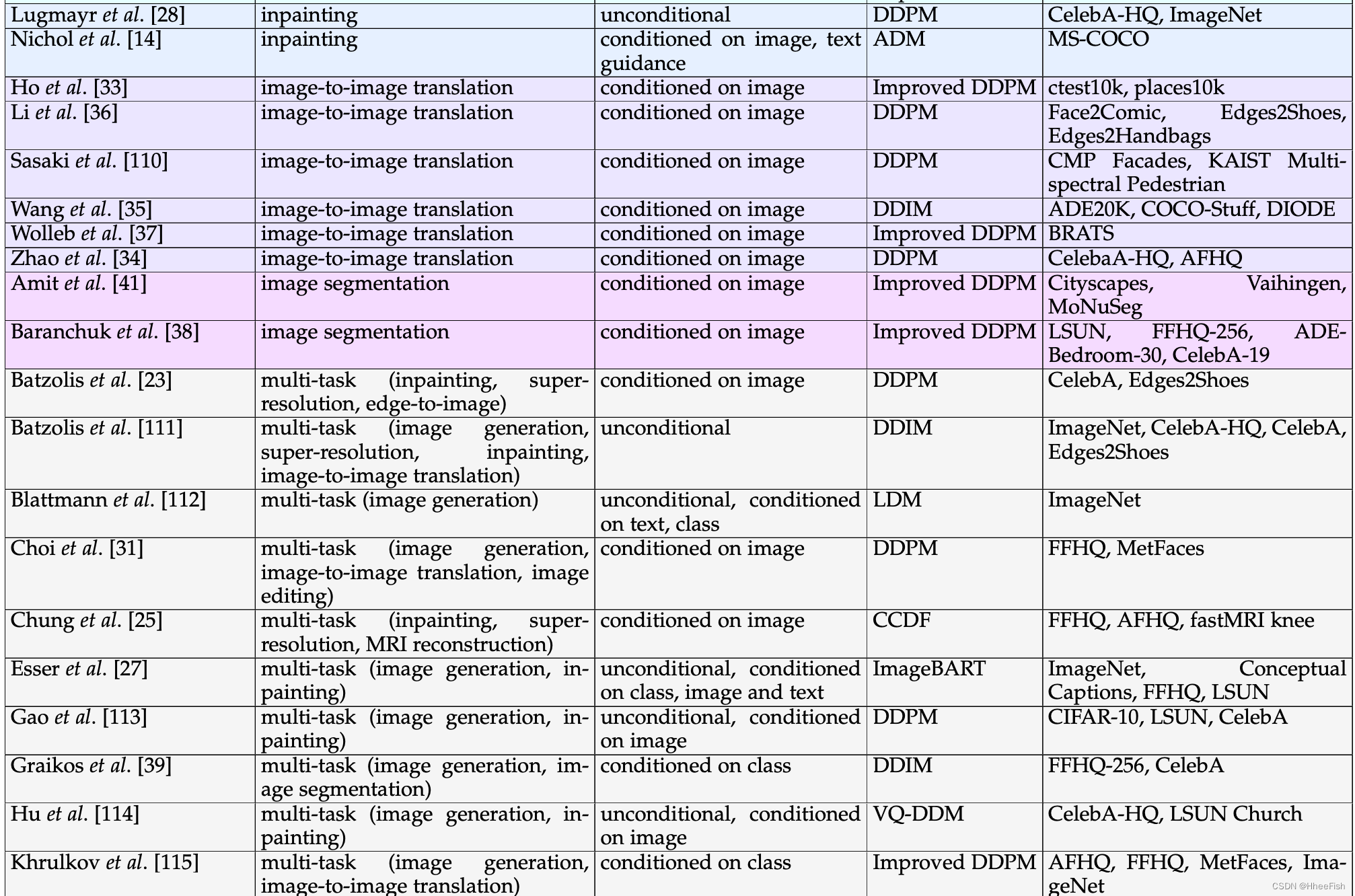
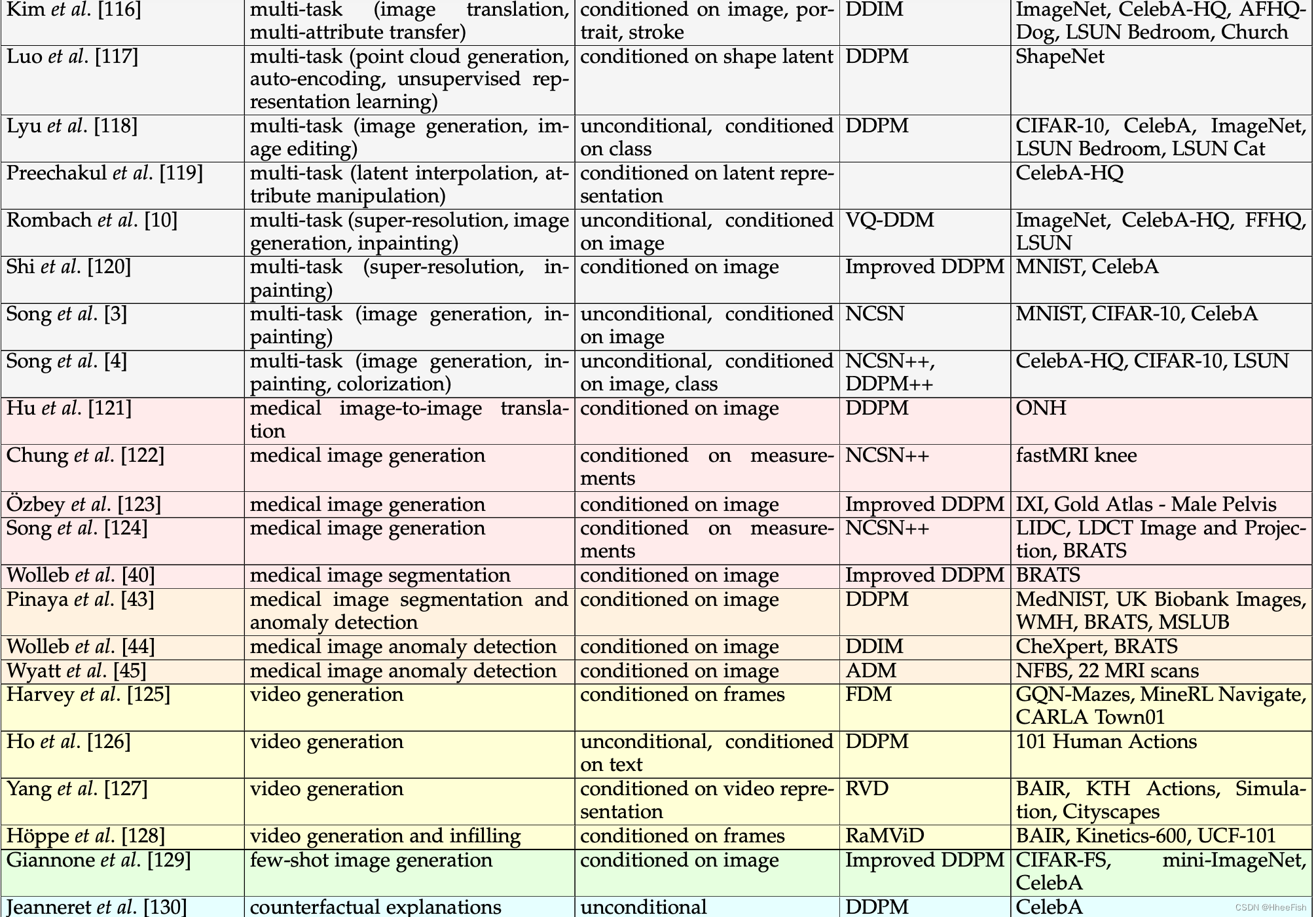
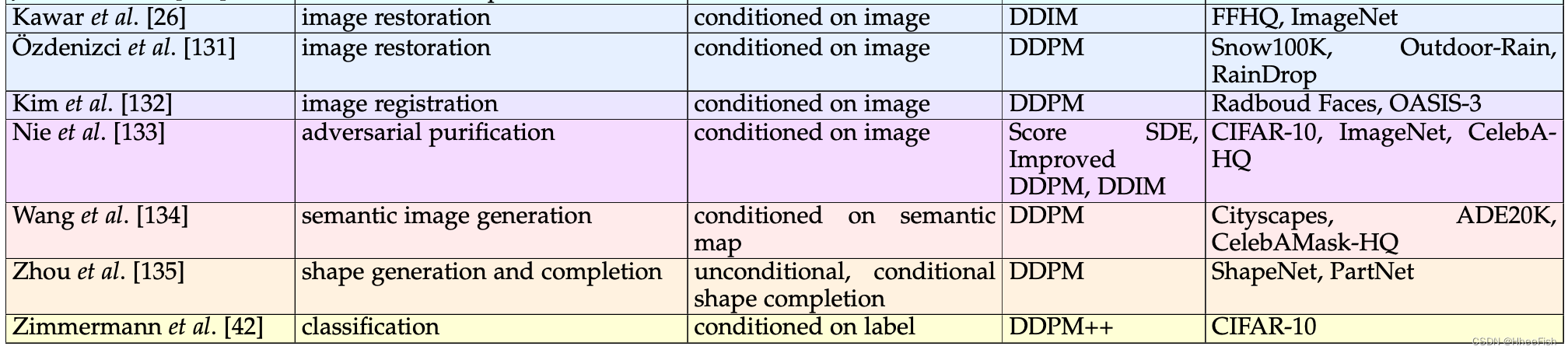
表1我们在计算机视觉中应用的扩散模型的多视角分类。为了对现有模型进行分类，我们考虑三个标准:任务、去噪条件和底层方法(体系结构)。此外，我们列出了应用调查模型的数据集。

我们将扩散模型分类为考虑不同分离标准的多视角分类法。也许分离模型最重要的标准是由(i)它们所应用的任务和(ii)它们所需的输入信号定义的。此外，由于制定扩散模型有多种方法，(iii)基础架构是对扩散模型进行分类的另一个关键因素。最后，在训练和评估中使用的数据集也非常重要，因为这有助于比较同一任务的不同基线。根据前面列举的标准，我们对扩散模型进行了分类，如表1所示。
在本节的其余部分中，我们提出了几个关于扩散模型的贡献，选择目标任务作为分离方法的主要标准。我们之所以选择这个分类标准，是因为它相当平衡，对扩散模型的研究具有代表性，便于从事特定任务的读者快速掌握相关工作。虽然主要任务通常与图像生成相关，但已经进行了大量的工作，以达到甚至超过GANs在其他方面的性能，如超分辨率、着色、图像编辑、图像间翻译或分割。

3.1.无条件图像生成

下面给出的扩散模型用于在无条件设置下生成样本。这种模型不需要监督信号，完全不受监督。我们认为这是图像生成的最基本和通用的设置
Sohlet等人的工作将扩散模型规范化为生成模型，学习反转马尔科夫链，将数据转换为高斯白噪声。他们的算法训练一个神经网络来预测反转马尔可夫链所需的高斯分布序列的均值和协方差。该神经网络基于一种包含多尺度卷积的卷积结构
Hoet al.[2]扩展了[1]中提出的工作，提议通过估计每一步图像中的噪声来学习反向过程。这一变化导致了一个类似于[3]中应用的去噪评分匹配的目标。为了预测图像中的噪声，作者使用了在[67]中介绍的Pixel-CNN+体系结构。
从相关工作[3]出发，Song等人提出了基于理论和实证分析的几个改进。他们解决了训练和采样两个阶段。在训练方面，作者展示了选择噪声尺度的新策略，以及如何将噪声条件纳入NCSNs[3]。对于采样，他们建议对参数应用指数移动平均，并选择Langevin dynamics的超参数，使步长验证某一方程。提出的变化解锁了NCSNs在高分辨率图像上的应用。
Jolicoeur-Martineau[79]引入了一个对抗目标和去噪分数匹配来训练基于分数的模型。此外，他们提出了一种新的采样方法，称为一致退火抽样，并证明了它比退火朗日文方法更稳定。他们的图像生成实验表明，新的目标在不影响多样性的情况下返回更高质量的示例。建议的更改在[2]、[3]、[13]中提出的体系结构上进行了测试。
Songet和[15]提高了基于分数的扩散模型的可能性。他们通过一个新的加权函数来实现这一目标，该函数将分数与损失相匹配。对于他们的图像生成实验，他们使用了[4]中引入的DDPM++体系结构。
Sinhaet等人[16]的工作提出了带有对比表示(D2C)的扩散解码模型，这是一种基于编码器产生的潜在表示训练扩散模型的生成方法。该框架基于[2]中提出的DDPM体系结构，通过将潜在表示映射到图像来生成图像。
DiffFlow是在[68]中引入的一种新的生成建模方法，它结合了归一化流和扩散概率模型。从扩散模型的角度来看，该方法的采样过程效率高达20倍，这得益于可学习的转发过程，跳过了不必要的噪声区域。作者使用与[2]中相同的体系结构进行了实验
在[76]中，作者提出了一个基于分数的生成视频模型作为迭代比例拟合(IPF)的实现，IPF是一种用于解决 Schrodinger（薛定谔） bridge问题的技术。这种新方法在图像生成和数据集插值上进行了测试，这是可能的，因为先验可以是任何分布。
Austin等人[72]在离散扩散模型上扩展了之前的方法[1]，研究了在正向过程中使用的过渡矩阵的不同选择。在图像生成任务中，他们的结果与之前的连续扩散模型具有竞争力。
Vahdat[17]训练潜在表征的扩散模型。他们使用一个隐空间编码和从隐空间解码。这项工作实现了高达56倍的采样速度。对于图像生成实验，作者采用了[4]中引入的NCSN++体系结构
在[2]中提出的工作之上，Nichol[6]引入了一些改进，发现线性噪声调度对于低分辨率来说是次优的。他们提出了一个新的选项，避免在转发过程结束时快速破坏信息。此外，他们还表明，为了提高扩散模型在对数似然方面的性能，需要学习方差。最后一个更改允许更快的采样，大约需要50个步骤
Song等[7]将[2]中使用的马尔可夫前进过程替换为非马尔可夫前进过程。生成过程的变化使模型首先预测正常样本，然后用来估计链的下一个步骤。这一变化导致了一个更快的采样过程，对生成的样本的质量影响很小。由此产生的框架被称为去噪扩散隐式模型(DDIM)。
Nachmani等人[87]的工作将扩散过程的高斯噪声分布替换为另外两个分布，即两个高斯分布和伽马分布的混合分布。结果表明，由于伽马分布具有较高的建模能力，其FID值更好，收敛速度更快。
Lam等人[84]学习了采样的噪声调度。训练的噪音时间表和以前一样保持线性。在对评分网络进行训练后，假设其接近最优值，以便将其用于噪声调度训练。推理由两个步骤组成。首先，通过固定两个初始超参数来确定调度。第二步是通常的反向过程，有确定的时间表。
Bond等人[74]提出了一个两阶段的过程，他们将矢量量化应用于图像以获得离散表示，并使用transformer[136]来逆转离散扩散过程，其中每个步骤的元素都是随机遮蔽的。采样过程更快，因为扩散应用于高度压缩的表示，这允许更少的去噪步骤(50-256)。
在[88]中，作者提出了一种估计推理时给定电流输入的噪声参数的方法。他们的改变改进了FID测量，同时需要更少的步骤。采用VGG-11估计噪声参数，DDPM[2]生成图像。
Jolicoeur-Martineau[80]引入了一种新的SDE解决方案，它介于的速度比Euler-Maruyama快2到5倍，它不影响生成的图像的质量。该求解器在一组用[3]预训练模型进行的图像生成实验中进行评估。
Watson[92]提出了一种动态规划算法，该算法能找到最优推理计划，时间复杂度为O(T)，其中T为步骤数。他们使用DDPM架构在cifar -10和ImageNet上进行了图像生成实验。
Wang等人[90]提出了一种基于 Schrodinger（薛定谔） bridge的新的深度生成模型。这是一个两阶段的方法，其中第一阶段学习目标分布的平滑版本，第二阶段派生实际目标。
Kingma等人[82]引入了一类扩散模型，可获得图像密度估计的最新似然。他们在网络的输入中加入傅立叶特征来预测噪声，并研究观察到的改进是否针对这类模型。他们的结果证实了这个假设，即。以前最先进的模型并没有从这种变化中受益。作为一项理论贡献，他们表明扩散损失仅通过其极值值受到信噪比函数的影响。
Dockhorn等[20]专注于基于分数的模型，通过在数据中添加另一个变量(速度)，利用临界阻尼朗之万扩散过程，这是该过程中唯一的噪音源。在新的扩散空间下，得到的分数函数被证明更容易学习。作者扩展了他们的工作，开发了一个更合适的分数目标称为混合分数匹配，以及一个抽样方法，通过集成解决SDE。作者采用了NCSN++和DDPM++体系结构来接受数据和速度，在无条件图像生成方面进行了评估，并优于类似的基于分数的扩散模型。
Xiao等人[93]试图提高采样速度，同时也保持了质量、覆盖率和多样性。他们的方法是在去噪过程中集成GAN，以区分真实样本(正向过程)和假样本(来自生成器的去噪样本)，目的是最小化被弱化的反向KL发散[137]。然而，通过直接生成干净的(完全去噪的)样本并在其上调节假样例来修改这一点。使用NCSN++体系结构和GAN发生器的自适应组归一化层，他们在图像合成和基于笔画的图像生成中实现了相似的Frechet起始距离(FID)值，采样速率比其他扩散模型快约20到2000倍。
由于高斯噪声分布导致高维基于分数的扩散模型存在局限性，Deasy等人[77]扩展了去噪分数匹配，以推广到正态噪声分布。通过增加更重的尾部分布，他们在几个数据集上的实验显示了有希望的结果，因为生成性能在某些情况下提高了(取决于分布的形状)。该方法擅长的一个重要场景是具有不平衡类的数据集
继文献[113]之后，Bao[19]提出了一个不需要使用非马尔可夫扩散过程进行训练的推理框架。首先推导出关于分数函数的最佳均值和方差的分析估计，并使用预先训练的基于分数的模型来获得分数值，他们展示了更好的结果，同时具有20到40倍的时间效率。用蒙特卡洛抽样逼近得分。然而，为了减少预训练的DPM模型的任何偏差，分数被裁剪在一些预先计算的边界内。
Watson等[8]首先介绍了如何在扩散模型的反向过程中集成重参数化技巧，以优化一系列快速采样器。他们使用核初始距离作为损失函数，展示了如何使用随机梯度下降进行优化。接下来，他们提出了一个特殊的参数化采样器家族，使用与以前相同的过程，它可以在较少的采样步骤下获得有竞争力的结果。使用FID和初始评分(IS)作为指标，该方法似乎优于一些扩散模型基线。
Zheng等人[94]建议在任意的步骤截断该过程，并提出了一种方法，通过放松将高斯随机噪声作为正向扩散的最终输出的约束，从该分布反扩散。为了解决从不可处理的分布开始反向过程的问题，使用隐式生成分布来匹配扩散数据的分布。代理分布适合通过GAN或条件传输。我们注意到生成器使用与扩散模型的采样器相同的U-Net模型，因此不添加额外的参数来训练。
Jing[29]试图通过减小扩散实现的空间本体，即减小扩散模型采样过程的持续时间。扩散过程的时间戳越大，子空间越小。数据被投射到有限的一组子空间，在特定的时间，每一个子空间都与一个分数模型相关联。在提高性能的同时，减少了计算成本。这项工作仅限于自然图像合成。对该方法在无条件图像生成中的性能进行了评价，结果表明，该方法在较低的推理时间下，与最先进的模型相比，取得了相似甚至更好的性能。该方法同样适用于inpaint任务。
Kim等人[81]提出将扩散过程改为非线性过程。这是通过使用一个可训练的规范化流模型来实现的，该模型在潜在空间中对图像进行编码，在那里它现在可以线性扩散到噪声分布。然后将类似的逻辑应用于去噪过程。该方法应用于NCSN++和DDPM++框架，而归一化流模型则基于ResNet。Deja等人[78]首先分析了扩散模型的逆向过程，并假设它有两个模型，一个产生器和一个降噪器。因此，他们建议将这个过程明确地分成两个部分:通过自动编码器的降噪器和通过扩散模型的生成器。这两个模型都使用相同的U-Net架构
Wang等人[91]从Arjovsky等人[138]和S?nderbye等人[139]提出的想法出发，通过添加噪声来增加鉴别器的输入数据。这是在[91]中通过从高斯混合分布注入噪声来实现的，高斯混合分布由不同时间步长的干净图像的加权扩散样本组成。噪声注入机制适用于真实图像和伪图像。实验在广泛的数据集上进行，以覆盖多分辨率和更高的分集
Ma等人[86]旨在使反向扩散过程更有效，同时保持合成性能。在基于分数的扩散模型家族中，他们开始分析频率域的反向扩散，随后在采样过程中应用空频滤波器，旨在整合初始噪声采样中目标分布的信息。作者使用NCSN[3]和NCSN++[4]进行了实验，在实验中，提出的方法清楚地显示了图像合成速度的提高(最多可减少20次采样步骤)，同时对低分辨率和高分辨率图像保持同样令人满意的生成质量

3.2.条件图像生成

接下来我们将展示应用于条件图像合成的扩散模型。这种情况通常基于各种源信号，在大多数情况下使用一些类标签。本文还讨论了执行无条件生成和条件生成的方法。
Dhariwal等[5]引入了一些架构更改来改进扩散模型的FID。他们还提出了分类器引导，在采样过程中使用分类器的梯度来引导扩散的策略。他们进行了无条件和有条件的图像生成实验。
Ho等人[99]介绍了一种不需要分类器的引导方法。它只需要一个条件扩散模型和一个无条件扩散模型，但他们使用相同的模型来学习这两种情况。在类标识符等于0的情况下训练无条件模型。该思想基于贝叶斯规则的隐式分类器。
Kong等人[83]定义了连续扩散步骤和噪声水平之间的双射。通过定义的双射，他们可以构建一个近似的扩散过程，所需的步骤更少。该方法使用之前的DDIM[7]和DDPM[2]架构对图像生成进行了测试。
Pandey[18]构建了一个生成器-细化器框架，其中生成器是一个VAE，细化器是一个受VAE输出制约的DDPM。由于DDPM只添加了细节，所以可以使用VAE的潜在空间来控制生成的图像的内容。经过对该框架的训练，得到的DDPM能够泛化到不同的噪声类型。更具体地说，如果反向过程不受不同噪声类型的影响，则DDPM能够重建初始图像。
liu等人[85]研究了使用常规数值方法求解反向过程的ODE公式。他们发现，与之前的方法相比，这些方法返回的样本质量更低。因此，他们引入了扩散模型的伪数值方法。他们的想法将数值方法分为两部分，梯度部分和转移部分。转移部分(标准方法有一个线性转移部分)被替换，以便结果尽可能接近目标流形。作为最后一步，他们展示了这种更改如何解决使用常规方法时发现的问题。
Ho等人[98]介绍了级联扩散模型(CDM)，这是一种以ImageNet类为条件生成高分辨率图像的方法。他们的框架包含多个扩散模型，其中来自管道的第一个模型生成基于图像类的低分辨率图像。后续的模型负责生成分辨率越来越高的图像。这些模型是有条件的类和低分辨率的图像。
Bordes等人[95]通过将自我监督任务可视化并将其与原始图像进行比较来检查其产生的表征。他们还会比较来自不同来源的表示。因此，使用扩散模型来生成以这些表示为条件的样本。作者对Dhariwal提出的U-Net架构进行了一些修改。[5]，例如添加条件批处理归一化层，并通过完全连接层映射向量表示。
Tachibana.[140]解决了ddpm的缓慢采样问题。他们建议通过增加随机微分方程求解器(去噪部分)的阶数(从1到2)来减少采样步骤的数量。在保留网络结构和分数匹配功能的同时，对采样器采用了Taylor展开格式，并代入了一些导数项，以简化计算。它们在保留性能的同时减少了后退步骤的数量。除了这些，另一个贡献是噪音时间表。
Benny等人[73]研究了在反向过程中预测图像而不是噪声的优缺点。他们得出结论，发现的一些问题可以通过插值两种类型的输出来解决。它们修改以前的体系结构，以返回噪声和图像，以及在执行插值时控制噪声重要性的值。该策略在DDPM和ddi体系结构之上进行评估。
文献[89]提出的方法允许扩散模型从数据集的低密度区域生成图像。他们使用两种新的损耗来引导反向过程。第一个损失引导扩散向低密度区域，而第二个损失强制扩散停留在流形上。此外，他们证明了扩散模型不能记住来自低密度社区的例子，生成新的图像。作者采用了一种类似于Dhariwal[5]的体系结构。
Choi等人[75]研究了噪声水平对通过扩散模型学习到的视觉概念的影响。他们将传统的目标函数加权方案修改为一种新的增强扩散模型以学习丰富的视觉概念的加权方案。该方法根据信噪比将噪声级分为三类(粗、含量和清理)。小信噪比为粗信噪比，中信噪比为含量信噪比，大信噪比为清理信噪比。权重函数将较低的权重分配给最后一组。
Karras等人[100]试图将基于扩散评分的模型分离为彼此独立的单个组件。这种分离允许在不影响其他单元的情况下修改单个部件，从而促进扩散模型的改进。在此框架下，作者首先提出了一个使用Heun方法作为ODE求解器的采样过程，在保持FID评分的同时减少了神经功能评估。他们进一步表明，随机抽样过程带来了巨大的性能效益。第二个贡献是通过对神经网络的输入和相应的目标进行预处理，以及使用图像增强来训练基于分数的模型。在无条件和类条件图像生成的背景下，
Salimans等人[103]提出了一种减少采样步骤数量的技术。他们将训练有素的教师模型的知识(用确定性DDIM表示)提取到学生模型中，该模型具有相同的体系结构，但采样步骤减少了一半。换句话说，学生的目标是走老师的两个连续步骤。此外，这个过程可以重复，直到达到所需的采样步骤数，同时保持相同的图像合成质量。最后，为了简化蒸馏过程并减少采样步骤(从8192步减少到4步)，研究了模型的三个版本和两个损失函数。
Song等人[4]和Dhariwal等人[5]基于分类器指导的基于分数的条件扩散模型的工作启发了Chao等人[97]开发了一个新的训练目标，以减少分数模型和真实分数之间的潜在差异。分类器的损失被修正为一个缩放的交叉熵，添加到修正的分数匹配损失。
Singh等人[104]提出了一种新的条件图像生成方法。他们提出了一种方法来调节噪声信号(从采样开始)，而不是在整个采样过程中调节信号。使用反演梯度[141]，噪声被注入关于有条件类的定位和方向的信息，同时保持相同的随机高斯分布。
Campbell等人[96]演示了一种连续时间的去噪扩散模型模拟，该模型能够处理离散数据。该工作通过一个跃迁率矩阵来模拟正向连续马尔可夫链扩散过程，通过反跃迁率矩阵的参数逼近来模拟反向去噪过程。进一步的贡献与训练目标、矩阵结构和优化采样器有关。
由Song等人[4]提出的将扩散模型解释为ODEs的方法被Lu等人[102]重新表述为一种可以用指数积分器求解的形式。这项工作的其他贡献是使用泰勒展开(一阶到三阶)近似新公式的积分项的ODE求解器，以及适应时间步计划的算法，速度是4到16倍。
Liu等人[21]描述了扩散模型和基于能量的模型的相似功能，并利用后者的复合结构，提出将多个扩散模型结合起来进行条件图像合成。在相反的过程中，多个扩散模型的组合，每个模型都与一个不同的条件相关联，可以通过连接或反连接来实现。

3.3.文本到图像的合成

到目前为止，已有相当数量的以文本为条件的扩散模型被开发出来，证明了文本到图像合成的任务是多么有趣。也许扩散模型最令人印象深刻的结果是在文本到图像的合成中获得的，在那里组合不相关的概念的能力，如物体，形状和纹理，产生不同寻常的例子。为了证实这一说法，我们使用Imagen[107]生成了一个“石兔雕像坐在月亮上”的图像，结果如图3所示。
Guet等人[105]介绍了VQ-Diffusion模型，这是一种文本到图像合成的方法，不具有以往方法的单向偏差。该方法利用其屏蔽机制，避免了推理过程中误差的累积。该模型分为两个阶段，第一个阶段是基于VQ-VAE学习通过离散标记来表示图像，第二个阶段是基于VQ-VAE的离散潜在空间的离散扩散模型。扩散模型的训练是以标题的嵌入为条件的。受掩码语言建模的启发，一些标记被替换为[掩码]标记。
Avrahami[30]提出了一种基于CLIP文本嵌入生成的图像嵌入的文本条件扩散模型[142]。这是一个两阶段的方法，其中第一阶段生成图像嵌入层，第二阶段(解码器)生成基于图像嵌入和文本标题的最终图像。为了实现图像的嵌入，作者使用了潜空间中的扩散模型。他们执行一个主观的人类评估来评估他们的生成结果。
Imagen在[107]中被引入作为文本到图像合成的一种方法。它由一个用于文本序列的编码器和一个用于生成高分辨率图像的扩散模型级联组成。这些模型也受编码器返回的文本嵌入的制约。此外，作者还介绍了一组新的标题(DrawBench)，用于文本到图像的评估。在该体系结构方面，作者开发了高效U-Net以提高效率，并将该体系结构应用于文本到图像生成的实验中。
为了解决扩散模型采样缓慢的不便，zhang等人[108]将工作重点放在了一种新的离散化方案上，该方案减少了误差并允许更大的步长，即。较低的采样步骤数。通过在评分函数中使用高阶多项式外推和指数积分器求解反向SDE，在保持生成能力的同时，大幅减少了网络评估的数量。
Shi[9]结合VQ-VAE[143]和扩散模型来生成图像。从VQ-VAE开始，编码功能被保留，而解码器被扩散模型取代。作者使用了来自[6]的u - network架构，将图像令牌注入到中间的块中。
在[112]中提出的工作基础上，Rombach等人引入了一种修改，使用相同的程序创建艺术图像:从数据库中提取图像的CLIP[142]潜在空间中的k近邻，然后通过使用这些嵌入引导反向去噪过程生成新图像。由于CLIP的潜在空间是由文字和图像共享的，所以扩散也可以通过文字提示进行引导。然而，在推断时，数据库被替换为另一个包含艺术图像的数据库。因此，模型在新数据库的样式内生成图像。
jiang等人[22]提出了一个框架来生成具有丰富服装表示的全身人体图像，并给出了三种输入:人体姿势、服装形状的文本描述和服装纹理的另一种文本。该方法的第一阶段将前一个文本提示符编码为一个嵌入向量，并将其注入生成表单映射的模块(基于编码器-解码器)。在第二阶段，基于扩散的转换器从多个多级代码本(每个特定于一个纹理)中对后一个文本提示符的嵌入表示采样，VQ-VAE[143]提出了一种机制。最初，对较粗级别的码本索引进行采样，然后使用前馈网络预测较细级别的索引。文本使用Sentence-BERT编码[144]。

3.4.图像超分辨率

Sahara等人[12]将扩散模型应用于超分辨率。他们的逆向过程学会了在低分辨率版本上生成高质量的图像。本研究采用[2]、[6]和以下数据集中的体系结构:CelebA-HQ、FFHQ和ImageNet。
Daniels等[24]使用基于分数的模型从两个分布的 Sinkhorn coupling 中取样。他们的方法是用神经网络对二元变量进行建模，然后解决最优运输问题。经过神经网络训练后，可以通过Langevin dynamics和基于分数的模型进行采样。他们使用U-Net架构进行图像超分辨率实验。

3.5.图像编辑

Meng[32]在各种引导图像生成任务中使用扩散模型，例如。笔画或以笔画为基础的写意和影像构图。从包含某种形式的引导的图像开始，它的属性(如形状和颜色)被保留下来，而变形通过逐步添加噪声(扩散模型的正向过程)被平滑掉。然后，对结果进行降噪(反向处理)，根据引导生成真实的图像。通过求解反向SDE，用通用扩散模型合成图像，不需要任何自定义数据集或修改训练。
[30]介绍了基于自然语言描述编辑图像特定区域的第一个方法之一。要修改的区域是由用户通过一个掩码指定的。该方法依赖于CLIP引导，根据文本输入生成图像，但作者观察到，将输出与原始图像结合在一起不能产生全局相干的图像。因此，他们修改去噪过程来解决这个问题。更精确地说，在每一步之后，作者在潜在图像上应用了maskon，同时添加了原始图像的噪声版本。
扩展[10]中提出的工作，Avrahami[109]将潜扩散模型应用于文本低水平编辑图像。一个VAE编码图像和自适应时间掩模(区域编辑)到潜在空间的扩散过程发生。每个样本都被迭代去噪，同时在感兴趣区域内的文本指导下。然而，受混合扩散[30]的启发，图像与当前时间步上被噪声干扰的潜在空间中的被屏蔽区域相结合。最后，对样本进行编码，生成新的图像。该方法演示了优越的性能，同时相对更快。

3.6.图像着色

Nichol[14]训练了一个以文本描述为条件的扩散模型，并研究了无分类器和基于clip的引导的有效性。他们用第一种选择获得了更好的结果。此外，他们微调模型的图像嵌入，解锁基于文本输入的图像修改。
Lugmay[28]提出了一种不确定掩模形式的嵌入方法。他们使用了一个无条件扩散模型，但是修改了它的反向过程。他们通过从掩模图像中采样已知区域来生成步进?1的图像，通过对步进图像进行去噪来生成未知区域。通过这个过程，作者观察到未知区域具有正确的结构，但语义也不正确。此外，他们通过多次重复提出的步骤来解决这个问题，在每次迭代中，他们用从步骤?1生成的去噪版本中获得的新样本替换之前的步骤中的图像。

3.7.图像到图像的翻译

Sahara等人[33]提出了一个使用扩散模型的图像间翻译框架，关注四个任务:着色、inpainting、un裁剪和JPEG恢复。建议的框架在所有四个任务中都是相同的，这意味着它不受每个任务的定制更改的影响。作者首先比较了L₁和L₂的损失，认为L₂是首选，因为它导致了更高的样本多样性。最后，他们再次确认了自我注意层在条件图像合成中的重要性。
为了翻译一组未配对的图像，Sasaki[110]提出了一种涉及两个联合训练的扩散模型的方法。在反向去噪过程中，每个模型在每一步都以另一个模型的中间样本为条件。此外，利用循环一致性损失对扩散模型的损失函数进行正则化[145]。
Zhao[34]的目的是通过利用具有同等重要意义的源域数据，改进当前基于图像到图像翻译得分的扩散模型。在源域和目标域上训练的基于能量的函数被用来指导SDE求解器。这导致生成的图像保留了域不可知的特征，同时将特定于源域的特征翻译到目标域。能量函数基于两个特征提取器，每个特征提取器特定于一个领域。
Wang[35]利用预训练的力量，使用GLIDE模型[14]进行训练，获得丰富的语义潜空间。从预先训练的版本开始，并替换头部以适应任何条件输入，模型在某些特定的下游图像生成任务上进行微调。这分两个步骤完成，第一步是冻结解码器，只训练新的编码器，第二步是同时训练它们。最后，采用对抗性训练和规范化无分类引导的方法来提高生成质量。
Li等人[36]介绍了一个基于布朗桥和GANs的图像到图像翻译的扩散模型。提出的过程首先用VQ-GAN编码图像[146]。在这个量化的潜空间中，扩散过程被表述为布朗桥，在源域和目标域的潜表示之间映射。最后，用另一种VQ-GAN对量化后的矢量进行解码，从而在新的域内合成图像。这两种GAN模型在各自的特定领域进行了独立训练。
继续他们之前在[44]中提出的工作，Wolleb等[37]扩展扩散模型，用特定于任务的另一个模型替换分类器。因此，在采样过程的每一步，都注入了任务特定网络的梯度。该方法使用回归器(基于编码器)或分割模型(使用U-Net架构)进行演示，而扩散模型基于现有框架[2]、[6]。这种设置的优点是，除了特定于任务的模型外，不需要再训练整个扩散模型。

3.8.图像语义分割

Baranchuk等[38]演示了如何在语义分割中使用扩散模型。从U-net的解码器(用于去噪过程)中获取不同尺度的特征映射(中间块)，并将它们连接起来(对特征映射进行上采样以获得相同的维度)，它们可以通过进一步附加多层感知器集成来对每个像素进行分类。作者表明，在去噪过程的后期提取的这些特征映射包含丰富的表示。实验表明，基于扩散模型的分割效果优于大多数基线
Amit[41]通过扩展U-Net编码器的架构，提出使用扩散概率模型进行图像分割。输入图像和当前估计图像经过两个不同的编码器，通过求和的方式组合在一起。然后将结果提供给U-Net的编码器-解码器。由于在每个时间步中都注入了随机噪声，对单个输入图像生成多个样本，并用于计算平均分割图。Unet架构基于之前的工作[6]，而输入功率生成器是用残差密集块(Residual density Blocks)构建的[147]。去噪样本发生器是一个简单的二维卷积层。

3.9.多任务方法

一系列扩散模型已被应用于多任务，显示出良好的跨任务泛化能力。我们将在下面讨论这种贡献。
Song等[3]提出了噪声条件评分网络(NCSN)，一种估计不同噪声尺度下评分函数的方法。对于采样，他们引入了一个退火版本的朗之万动力学，并使用它来报告图像生成和inpainting的结果。NCSN主要基于[148]中提出的工作，有一些小的变化，如用实例规范化替换批处理规范化。
[4]中引入的扩散模型SDE公式推广了以前的几种方法[1]-[3]。Song等[4]将正向和反向扩散过程作为sde的解。这种技术解锁了新的采样方法，如预测校正采样器，或基于ode的确定性采样器。作者对图像的生成、绘制和着色进行了实验。
Esser[27]提出了一种生成模型ImageBART，它学会在紧凑的图像表示上恢复多项式扩散过程。使用一个转换器对反向步骤进行自回归建模，其中编码器的表示是使用前一步的输出获得的。ImageBART在无条件、类条件和文本条件的图像生成以及本地编辑方面进行评估。
Gao等人[113]引入了扩散恢复似然，这是基于能量的模型的一种新的训练方法。他们学习一系列基于能量的扩散过程边缘分布模型。因此，他们从基于边缘能量的模型中推导出条件分布，而不是用正态分布近似相反的过程。作者进行了图像生成和inpainting两方面的实验。
Batzolis等人[23]分析了之前基于分数的条件图像生成扩散模型。此外，他们还提出了一种新的条件图像生成方法——条件多速度扩散估计(CMDE)。该方法是基于对目标图像和条件图像以相同速率扩散的观察，可能是次优的。因此，他们提出用SDE对两幅具有相同漂移和不同扩散率的图像进行扩散。该方法在嵌入、超分辨率和边缘图像合成等方面进行了评价。
Liu等人[101]引入了一个框架，允许从参考图像中进行文本、内容和风格指导。其核心思想是使用最大化图像和文本所学表示之间相似性的方向。图像和文本嵌入由CLIP模型[142]生成。为了满足在噪声图像上训练CLIP的需要，作者提出了一种不需要文本字幕的自我监督程序。该程序使用一对正常图像和一对带噪图像来最大化正片对之间的相似性，并最小化负片对（对比目标）
Choi[31]提出了一种不需要进一步训练的新方法，用于使用无条件扩散模型进行条件图像合成。给定一个referenceimage,即。在这种情况下，通过消除低频内容并将其替换为参考图像中的内容，每个样本都更接近它。低通滤波器由一个下采样操作表示，然后是一个相同因子的上采样滤波器。作者展示了该方法如何应用于各种图像到图像的翻译任务，例如。画到图像，并与涂鸦。
Hu.[114]建议将扩散模型应用于离散的VAE给出的离散表示。考虑到CelebA-HQ和LSUN Church的数据集，他们在图像生成和填充实验中评估了这个想法。
Rombach[10]引入了潜在扩散模型，其中正向和反向过程发生在自动编码器学习的潜在空间上。它们还包括在体系结构中的交叉注意，这带来了条件图像合成的进一步改进。该方法主要采用超分辨率、图像生成和图像修复技术。
Preechakul等人[119]介绍的方法包含一个学习描述性潜在空间的语义编码器。该编码器的输出用于约束DDIM的一个实例。该方法可以很好地完成插值或属性操作等任务。
Chung等[25]引入了一种采样算法，它减少了条件情况下所需的步骤数。与标准情况下的反向过程从高斯噪声开始相比，他们的方法首先执行一个向前的步骤来获得中间噪声图像，并从这一点开始继续采样。该方法在嵌入、超分辨率和mri重建上得到了验证。
在[116]中，作者微调了预训练的DDIM，以根据文本描述生成图像。他们提出了一个局部定向的CLIP丢失，基本上强制生成的图像和原始图像之间的方向尽可能接近参考(原始域)和目标文本(目标域)之间的方向。评价中考虑的任务是图像在不可见域之间的翻译和多属性转换。
从Meng等人[32]的扩散模型SDEs的制定开始，Khrulkovet等人[115]研究了潜在空间和由此产生的编码器映射。根据蒙格公式，它表明这些编码器映射是最优传输映射，但这只是证明了多变量正态分布。作者利用Dhariwal[5]的模型实现，通过数值实验和实际实验进一步支持这一观点。
Shi等人[120]首先观察了如何将一个基于分数的无条件扩散模型表述为Schrodinger bridge，该桥可以使用修正版的迭代比例拟合来求解。之前的方法被重新表述为接受一个条件，从而使条件综合成为可能。对迭代算法进行了进一步的调整，以优化收敛所需的时间。该方法首先用Kovachki等人[149]的合成数据进行了验证，显示出在估计地面真相方面改进了的能力。作者还进行了超分辨率、灌注和生化需氧量的实验，后者的任务受到Marzouk等人[150]的启发。
受到检索transformer[151]的启发，Blattmann等人[112]提出了一种训练扩散模型的新方法。首先，利用最近邻算法从数据库中提取一组相似的图像;图像由一个具有固定参数的编码器进一步编码，并投影到CLIP[142]特征空间。最后，扩散模型的反向过程取决于这个潜在空间。该方法可以进一步扩展到使用其他条件信号，如。文本，通过简单地用信号的编码表示增强潜在空间。
Lyu等人[118]引入了一种新的技术来减少扩散模型的采样步骤数，同时提高了性能。这个想法是阻止扩散过程在早期的步骤。由于采样不能从随机高斯噪声开始，因此使用GAN或VAE模型将最后的扩散图像编码到高斯潜空间中。然后将结果解码为一幅图像，该图像可扩散到向后处理的起始点。Graikoset al.[39]的目的是将扩散模型分离为两个独立的部分，一个先验(基础部分)和一个约束(条件)。这使得模型无需进一步训练就可以应用于各种任务。将DDPM的方程从[2]改为独立训练模型，并在条件设置中使用它，前提是约束变得可微。作者进行了条件图像合成和图像分割的实验。
Batzolis等人[111]在扩散模型中引入了一种新的正向过程，称为非均匀扩散。这是由每个像素用不同的sde扩散决定的。在这个过程中使用了多个网络，每个网络对应不同的扩散尺度。本文进一步论证了一种新的条件采样器，它将两种基于分数的去噪采样方法插在了一起。该模型的体系结构基于[2]和[4]，通过无条件合成、超分辨率、内嵌和边-像平移进行了评价。

3.10.医学图像生成与翻译

Wolleb等[40]介绍了一种基于扩散模型的脑肿瘤图像分割方法。训练过程包括对分割图进行扩散，然后去噪得到原始图像。在向后处理过程中，大脑MR图像被连接到中间去噪步骤，以便通过U-Net模型，从而使去噪过程以其为条件。此外，对于每个输入，作者建议生成多个样本，由于随机性，这些样本会有所不同。因此，集成可以生成一个平均分割映射及其方差(与映射的不确定性相关)。
Song等人[124]介绍了一种基于分数的模型方法，该方法能够解决医学成像中的逆问题，即。根据测量重建图像。首先，训练一个无条件评分模型。然后，推导了测量的随机过程，该过程可用于通过近端优化步骤向模型中注入条件信息。最后，将信号与测量之间的映射矩阵进行分解，以实现封闭形式的采样。作者对不同的医学图像类型进行了多次实验，包括CT、低剂量CTand MRI。在医学成像领域内，但主要关注从加速MRI扫描重建图像，
Chung等人[122]提出使用基于分数的扩散模型解决逆问题。评分模型只在无条件设置的震级图像上进行预训练。然后，在采样过程中采用方差爆炸SDE求解器[4]。通过采用预测校正算法[4]与数据一致性映射交织，分割图像(实部和虚部)通过馈入，使模型对测量进行调节。此外，作者提出了该方法的一种扩展，它可以对多个线圈变化的测量进行调节。
Ozbey等人[123]提出了一种带有对抗性推理的扩散模型。受[93]的启发，为了增加每个扩散步骤，从而减少步骤，作者在反向过程中使用GAN模型来估计每一步去噪后的图像。使用与[145]类似的方法，他们引入了一种周期一致的体系结构，以允许在未配对的数据集上进行训练。
Hu等[121]的目的是去除光学相干层析(OCT) b扫描中的散斑噪声。第一阶段由一种称为自融合的方法表示，如[152]所述，其中选择靠近输入OCT体积的给定2D切片的额外b扫描。第二阶段由扩散模型组成，其起点是原始b扫描及其邻近区域的加权平均值。因此，噪声可以通过采样一个干净的扫描来去除。

3.11.医学图像异常检测

自动编码器被广泛用于异常检测[153]。由于扩散模型可以被视为特殊类型的VAEs，似乎也很自然地使用扩散模型来完成相同的任务。到目前为止，扩散模型在检测医学图像中的异常方面显示出了有希望的结果，下文将进一步讨论。
Wyatt等[45]用健康的医疗图像训练DDPM。在推断时通过从原始图像中减去生成的图像来检测异常。研究还证明了用单纯形噪声代替高斯噪声对这类任务有更好的效果。
Wolleb等[44]提出了一种基于扩散模型的弱监督方法用于医学图像异常检测。给出两个未配对的图像，一个是健康的，一个是有病变的，前者被模型扩散。然后，利用二值分类器的梯度来引导去噪过程，以生成健康图像。最后，将样本健康图像与病灶图像相减得到异常图。
Pinaya[43]提出了一种基于扩散的方法来检测大脑扫描中的异常，并分割这些区域。用VQ-VAE[143]对图像进行编码，并从编码簿中获得量化的潜在表示。扩散模型在这个潜在空间中起作用。对反向过程中值步骤的中间样本进行平均，然后应用预计算的阈值映射，生成一个隐含异常位置的二元掩码。从中间开始反向处理，二进制掩码用于去噪异常区域，同时保持其余区域。最后，对最后一步的样本进行解码，得到健康的图像。将输入图像与合成图像相减，得到异常分割图

3.12.视频生成

最近的进展使扩散模型更有效，使其在视频领域的应用成为可能。接下来我们将介绍将扩散模型应用于视频生成的工作。Ho等人[126]将扩散模型引入到视频生成任务中。与2D情况相比，更改只应用于体系结构。作者采用了[154]中的3D U-Net，给出了非条件和文本条件视频生成的结果。较长的视频以自回归的方式生成，其中后一个视频块以前一个视频块为条件。
Yang[127]使用扩散模型逐帧生成视频。反向过程完全取决于卷积递归神经网络提供的上下文向量。作者进行了消融研究，以确定预测下一帧的残差是否比预测实际帧的结果更好。
Hoppe等人[128]提出了一种可用于视频生成和填充的随机掩膜视频扩散(RaMViD)方法。他们工作的主要贡献是一种新的训练策略，即随机地将帧划分为掩模帧和非掩模帧。未掩模帧用于调节扩散，掩模帧通过正向过程进行扩散。
Harvey等人[125]的工作引入了灵活的扩散模型，这是一种可用于长视频生成的多种采样方案的扩散模型。如[128]所述，作者通过随机选择用于扩散的帧和用于调节过程的帧来训练扩散模型。在训练模型之后，他们研究了多种采样方案的有效性，得出的结论是，采样的选择取决于数据集

3.13.其他任务

有一些开创性的工作将扩散模型应用到新的任务中，这些工作很少通过扩散模型进行探索。我们将在下面收集和讨论这些贡献。
luo等人[117]将扩散模型应用于3D点云生成、自动编码和无监督表示学习。他们从点云的可能性的变分下界推导出一个目标函数，该下界以形状潜势为条件。实验使用PointNet[155]作为底层架构进行。
zhou等人[135]介绍了点体素扩散(Point-Voxel Diffusion, PVD)，一种应用扩散点体素表示的形状生成新方法。该方法解决了在ShapeNet和PartNet数据集上的形状生成和完成任务。
Zimmermann[42]展示了一种应用基于分数的模型进行分类的策略。他们将图像标签作为条件变量添加到评分函数中，由于ODE公式，可以在推理时计算出条件似然。因此，预测被标记为最大似然。此外，他们研究了这种类型的分类器对非分布场景的影响，考虑到常见的图像损坏和对抗性扰动。
Kim等人[132]提出使用扩散模型解决图像配准任务。这是通过两个网络实现的，一个是根据[2]的扩散网络，一个是基于U-Net的变形网络，如[156]所述。给定两幅图像(一幅静态，一幅动态)，前者的作用是评估两幅图像之间的变形，并将结果反馈给后者，后者预测变形场，从而生成样本。该方法还具有综合整个过渡过程中的变形的能力。作者对不同的任务进行了实验，一个是2D面部表情，一个是3D大脑图像。结果表明，该模型能够产生定性和准确的配准场。
Jeanner等人[130]将扩散模型应用于反事实解释。该方法从一个有噪声的查询图像开始，并生成一个具有无条件ddpm的样本。用生成的样本，计算制导所需的梯度。然后，应用反引导过程的一个步骤。输出将在接下来的反向步骤中进一步使用。
Nie等人[133]论证了扩散模型如何被用作对抗攻击的防御机制。给定一个对抗性图像，它被扩散到一个最佳计算的时间步长。结果被模型逆转，最后产生一个提纯的样品。为了优化求解逆时SDE的计算，采用了Liet等人[157]的伴随灵敏度方法进行梯度评分计算。
在少镜头学习的背景下，Giannone提出了一种基于扩散模型的图像生成器。[129]。给定一小组图像作为合成的条件，一个视觉转换器对这些图像进行编码，然后产生的上下文表示(通过两种不同的技术)集成到去噪过程中使用的U-Net模型中。
Wang等人[134]提出了一种基于扩散模型的语义图像合成框架。利用扩散模型的u -网络体系结构，输入噪声被提供给编码器，而语义标签映射使用多层空间自适应规范化操作符传递给解码器[158]。为了进一步改善采样质量和语义标签映射上的条件，还为采样方法提供了一个空映射来产生无条件噪声。然后，最后的噪声使用这两个估计。
关于恢复受各种天气条件(如雪、雨)负面影响的图像的任务，Ozdenizci等人[131]演示了如何使用扩散模型。他们通过在每个时间步中将降级图像的通道连接到去噪样本，从而对降级图像的去噪过程进行条件化。为了处理不同大小的图像，在每一步，样本被分成重叠的小块，通过模型并行传递，并通过重叠像素的平均组合回来。所采用的扩散模型基于U-Net架构，如[2]，[4]所示，但修改为接受两个连接的图像作为输入。
Kawar等人[26]将图像恢复任务定义为线性逆问题，提出使用扩散模型。受Kawar等[159]的启发，采用奇异值分解法对线性退化矩阵进行分解，使得输入和输出都可以映射到进行扩散过程的矩阵的光谱空间上。利用[2]和[5]中预训练的扩散模型，对各种任务进行了评估:超分辨率、去模糊、着色和inpainting。

3.14.理论贡献

huang等人[58]演示了song等人[4]提出的方法是如何与最大化反向SDE边际似然的下界相联系的。此外，他们还通过CIFAR-10和MNIST上的图像生成实验验证了他们的理论贡献。

4.结束语和未来方向

本文综述了扩散模型在计算机视觉领域的研究进展。我们确定了三种主要的扩散建模公式:DDPM, NCSN和SDE。每个公式在图像生成方面都取得了显著的效果，在增加生成样本的多样性的同时，超过了ganss。扩散模型在研究尚处于早期阶段时就取得了突出的成果。虽然我们注意到主要的焦点是有条件和无条件的图像生成，但仍有许多任务需要探索和进一步的改进

4.1.局限

扩散模型最显著的缺点仍然是需要在推理时间内执行多个步骤来生成一个样本。尽管在这个方向上进行了大量的研究，但GANs在生成图像方面仍然更快。扩散模型的其他问题可以与使用剪辑嵌入进行文本到图像生成的常用策略联系起来。例如，rameset等人[106]强调，他们的模型很难在图像中生成可读的文本，并通过声明CLIP嵌入不包含关于拼写的信息来激发这种行为。因此,当这样的嵌入被用来调节去噪过程，模型可以继承这类问题。

4.2.未来方向

除了目前研究更有效扩散模型的趋势外，未来的工作可以研究扩散模型在其他计算机视觉任务中的应用，如图像去雾化、视频异常检测或视觉问题回答。即使我们发现了一些研究医学图像[43]-[45]异常检测的工作，这一任务也可以在其他领域进行探索，如视频监控或工业检查。
一个有趣的研究方向是评估扩散模型在辨别任务中学习到的表示空间的质量和效用。这至少可以通过两种不同的方式实现。直接的方法是在去噪模型提供的潜在表征上学习一些判别模型，以解决一些分类或回归任务。以一种间接的方式，通过用扩散模型生成的真实样本增强训练集。后一个方向可能更适合于诸如物体检测等任务，在这些任务中，嵌入扩散模型可以很好地融合图像中的新物体。
未来的另一个工作方向是利用条件扩散模型在视频中模拟可能的未来。生成的视频可以进一步作为强化学习模型的输入

参考文献

[1]J. Sohl-Dickstein, E. Weiss, N. Maheswaranathan, and S. Ganguli,“Deep unsupervised learning using non-equilibrium thermody-namics,” inProceedings of ICML, pp. 2256–2265, 2015.
[2]J. Ho, A. Jain, and P. Abbeel, “Denoising diffusion probabilisticmodels,” inProceedings of NeurIPS, vol. 33, pp. 6840–6851, 2020.
[3]Y. Song and S. Ermon, “Generative modeling by estimatinggradients of the data distribution,” inProceedings of NeurIPS,vol. 32, pp. 11918–11930, 2019.
[4]Y. Song, J. Sohl-Dickstein, D. P. Kingma, A. Kumar, S. Ermon, andB. Poole, “Score-Based Generative Modeling through StochasticDifferential Equations,” inProceedings of ICLR, 2021.
[5]P. Dhariwal and A. Nichol, “Diffusion models beat gans on imagesynthesis,” inProceedings of NeurIPS, vol. 34, pp. 8780–8794, 2021.
[6]A. Q. Nichol and P. Dhariwal, “Improved denoising diffusionprobabilistic models,” inProceedings of ICML, pp. 8162–8171,2021.
[7]J. Song, C. Meng, and S. Ermon, “Denoising Diffusion ImplicitModels,” inProceedings of ICLR, 2021.
[8]D. Watson, W. Chan, J. Ho, and M. Norouzi, “Learning fastsamplers for diffusion models by differentiating through samplequality,” inProceedings of ICLR, 2021.
[9]J. Shi, C. Wu, J. Liang, X. Liu, and N. Duan, “DiVAE: Photoreal-istic Images Synthesis with Denoising Diffusion Decoder,”arXivpreprint arXiv:2206.00386, 2022.
[10]R. Rombach, A. Blattmann, D. Lorenz, P. Esser, and B. Ommer,“High-Resolution Image Synthesis with Latent Diffusion Mod-els,” inProceedings of CVPR, pp. 10684–10695, 2022.
[11]R. Rombach, A. Blattmann, and B. Ommer, “Text-Guided Syn-thesis of Artistic Images with Retrieval-Augmented DiffusionModels,”arXiv preprint arXiv:2207.13038, 2022.
[12]C. Saharia, J. Ho, W. Chan, T. Salimans, D. J. Fleet, andM. Norouzi, “Image super-resolution via iterative refinement,”arXiv preprint arXiv:2104.07636, 2021.
[13]Y. Song and S. Ermon, “Improved techniques for training score-based generative models,” inProceedings of NeurIPS, vol. 33,pp. 12438–12448, 2020.
[14]A. Nichol, P. Dhariwal, A. Ramesh, P. Shyam, P. Mishkin, B. Mc-Grew, I. Sutskever, and M. Chen, “GLIDE: Towards PhotorealisticImage Generation and Editing with Text-Guided Diffusion Mod-els,” inProceedings of ICML, pp. 16784–16804, 2021.
[15]Y. Song, C. Durkan, I. Murray, and S. Ermon, “Maximum likeli-hood training of score-based diffusion models,” inProceedings ofNeurIPS, vol. 34, pp. 1415–1428, 2021.
[16]A. Sinha, J. Song, C. Meng, and S. Ermon, “D2C: Diffusion-decoding models for few-shot conditional generation,” inPro-ceedings of NeurIPS, vol. 34, pp. 12533–12548, 2021.
[17]A. Vahdat, K. Kreis, and J. Kautz, “Score-based generative model-ing in latent space,” inProceedings of NeurIPS, vol. 34, pp. 11287–11302, 2021.
[18]K. Pandey, A. Mukherjee, P. Rai, and A. Kumar, “VAEs meetdiffusion models: Efficient and high-fidelity generation,” inPro-ceedings of NeurIPS Workshop on DGMs and Applications, 2021.
[19]F. Bao, C. Li, J. Zhu, and B. Zhang, “Analytic-DPM: an AnalyticEstimate of the Optimal Reverse Variance in Diffusion Probabilis-tic Models,” inProceedings of ICLR, 2022.
[20]T. Dockhorn, A. Vahdat, and K. Kreis, “Score-based generativemodeling with critically-damped Langevin diffusion,” inProceed-ings of ICLR, 2022
[21]N. Liu, S. Li, Y. Du, A. Torralba, and J. B. Tenenbaum, “Composi-tional Visual Generation with Composable Diffusion Models,” inProceedings of ECCV, 2022.
[22]Y. Jiang, S. Yang, H. Qiu, W. Wu, C. C. Loy, and Z. Liu,“Text2Human: Text-Driven Controllable Human Image Genera-tion,”ACM Transactions on Graphics, vol. 41, no. 4, pp. 1–11, 2022.
[23]G. Batzolis, J. Stanczuk, C.-B. Sch ?onlieb, and C. Etmann, “Con-ditional image generation with score-based diffusion models,”arXiv preprint arXiv:2111.13606, 2021.
[24]M. Daniels, T. Maunu, and P. Hand, “Score-based generativeneural networks for large-scale optimal transport,” inProceedingsof NeurIPS, pp. 12955–12965, 2021.
[25]H. Chung, B. Sim, and J. C. Ye, “Come-Closer-Diffuse-Faster:Accelerating Conditional Diffusion Models for Inverse Prob-lems through Stochastic Contraction,” inProceedings of CVPR,pp. 12413–12422, 2022.
[26]B. Kawar, M. Elad, S. Ermon, and J. Song, “Denoising diffusionrestoration models,” inProceedings of DGM4HSD, 2022.
[27]P. Esser, R. Rombach, A. Blattmann, and B. Ommer, “ImageBART:Bidirectional Context with Multinomial Diffusion for Autoregres-sive Image Synthesis,” inProceedings of NeurIPS, vol. 34, pp. 3518–3532, 2021.
[28]A. Lugmayr, M. Danelljan, A. Romero, F. Yu, R. Timofte, andL. Van Gool, “RePaint: Inpainting using Denoising DiffusionProbabilistic Models,” inProceedings of CVPR, pp. 11461–11471,2022.
[29]B. Jing, G. Corso, R. Berlinghieri, and T. Jaakkola, “Subspacediffusion generative models,”arXiv preprint arXiv:2205.01490,2022.
[30]O. Avrahami, D. Lischinski, and O. Fried, “Blended diffusion fortext-driven editing of natural images,” inProceedings of CVPR,pp. 18208–18218, 2022.
[31]J. Choi, S. Kim, Y. Jeong, Y. Gwon, and S. Yoon, “ILVR: Condi-tioning Method for Denoising Diffusion Probabilistic Models,” inProceedings of ICCV, pp. 14347–14356, 2021.
[32]C. Meng, Y. Song, J. Song, J. Wu, J.-Y. Zhu, and S. Ermon, “SDEdit:Guided Image Synthesis and Editing with Stochastic DifferentialEquations,” inProceedings of ICLR, 2021.
[33]C. Saharia, W. Chan, H. Chang, C. Lee, J. Ho, T. Salimans, D. Fleet,and M. Norouzi, “Palette: Image-to-image diffusion models,” inProceedings of SIGGRAPH, pp. 1–10, 2022.
[34]M. Zhao, F. Bao, C. Li, and J. Zhu, “EGSDE: Unpaired Image-to-Image Translation via Energy-Guided Stochastic DifferentialEquations,”arXiv preprint arXiv:2207.06635, 2022.
[35]T. Wang, T. Zhang, B. Zhang, H. Ouyang, D. Chen, Q. Chen,and F. Wen, “Pretraining is All You Need for Image-to-ImageTranslation,”arXiv preprint arXiv:2205.12952, 2022.
[36]B. Li, K. Xue, B. Liu, and Y.-K. Lai, “VQBB: Image-to-image Trans-lation with Vector Quantized Brownian Bridge,”arXiv preprintarXiv:2205.07680, 2022.
[37]J. Wolleb, R. Sandk ?uhler, F. Bieder, and P. C. Cattin, “The SwissArmy Knife for Image-to-Image Translation: Multi-Task Diffu-sion Models,”arXiv preprint arXiv:2204.02641, 2022.
[38]D. Baranchuk, I. Rubachev, A. Voynov, V. Khrulkov, andA. Babenko, “Label-Efficient Semantic Segmentation with Diffu-sion Models,” inProceedings of ICLR, 2022.
[39]A. Graikos, N. Malkin, N. Jojic, and D. Samaras, “Diffusionmodels as plug-and-play priors,”arXiv preprint arXiv:2206.09012,2022.
[40]J. Wolleb, R. Sandk ?uhler, F. Bieder, P. Valmaggia, and P. C. Cattin,“Diffusion Models for Implicit Image Segmentation Ensembles,”inProceedings of MIDL, 2022.
[41]T. Amit, E. Nachmani, T. Shaharbany, and L. Wolf, “SegDiff:Image Segmentation with Diffusion Probabilistic Models,”arXivpreprint arXiv:2112.00390, 2021.
[42]R. S. Zimmermann, L. Schott, Y. Song, B. A. Dunn, and D. A.Klindt, “Score-based generative classifiers,” inProceedings ofNeurIPS Workshop on DGMs and Applications, 2021.
[43]W. H. Pinaya, M. S. Graham, R. Gray, P. F. Da Costa, P.-D. Tudo-siu, P. Wright, Y. H. Mah, A. D. MacKinnon, J. T. Teo, R. Jager,et al., “Fast Unsupervised Brain Anomaly Detection and Segmen-tation with Diffusion Models,”arXiv preprint arXiv:2206.03461,2022.
[44]J. Wolleb, F. Bieder, R. Sandk ?uhler, and P. C. Cattin, “Diffu-sion Models for Medical Anomaly Detection,”arXiv preprintarXiv:2203.04306, 2022.
[45]J. Wyatt, A. Leach, S. M. Schmon, and C. G. Willcocks, “AnoD-DPM: Anomaly Detection With Denoising Diffusion ProbabilisticModels Using Simplex Noise,” inProceedings of CVPRW, pp. 650–656, 2022.
[46]Y. Bengio, A. Courville, and P. Vincent, “Representation learning:A review and new perspectives,”IEEE Transactions on PatternAnalysis and Machine Intelligence, vol. 35, no. 8, pp. 1798–1828,2013.
[47]I. Goodfellow, Y. Bengio, and A. Courville,Deep Learning. MITPress, 2016.
[48]G. E. Hinton and R. R. Salakhutdinov, “Reducing the dimension-ality of data with neural networks,”Science, vol. 313, no. 5786,pp. 504–507, 2006.
[49]D. P. Kingma and M. Welling, “Auto-Encoding VariationalBayes,” inProceedings of ICLR, 2014.
[50]I. Higgins, L. Matthey, A. Pal, C. P. Burgess, X. Glorot, M. M.Botvinick, S. Mohamed, and A. Lerchner, “beta-VAE: LearningBasic Visual Concepts with a Constrained Variational Frame-work,” inProceedings of ICLR, 2017
[51]I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville, and Y. Bengio, “Generative adver-sarial nets,” inProceedings of NIPS, pp. 2672–2680, 2014.
[52]M. Caron, I. Misra, J. Mairal, P. Goyal, P. Bojanowski, andA. Joulin, “Unsupervised learning of visual features by con-trasting cluster assignments,” inProceedings of NeurIPS, vol. 33,pp. 9912–9924, 2020.
[53]T. Chen, S. Kornblith, M. Norouzi, and G. Hinton, “A simpleframework for contrastive learning of visual representations,” inProceedings of ICML, vol. 119, pp. 1597–1607, 2020.
[54]F.-A.Croitoru,D.-N.Grigore,andR.T.Ionescu,“Discriminability-enforcing loss to improve representationlearning,” inProceedings of CVPRW, pp. 2598–2602, 2022.
[55]A. van den Oord, Y. Li, and O. Vinyals, “Representationlearning with contrastive predictive coding,”arXiv preprintarXiv:1807.03748, 2018.
[56]S. Laine and T. Aila, “Temporal ensembling for semi-supervisedlearning,” inProceedings of ICLR, 2017.
[57]A. Tarvainen and H. Valpola, “Mean teachers are better rolemodels: Weight-averaged consistency targets improve semi-supervised deep learning results,” inProceedings of NIPS, vol. 30,pp. 1195–1204, 2017.
[58]C.-W. Huang, J. H. Lim, and A. C. Courville, “A variationalperspective on diffusion-based generative models and scorematching,” inProceedings of NeurIPS, vol. 34, pp. 22863–22876,2021.
[59]Y. LeCun, S. Chopra, R. Hadsell, M. Ranzato, and F. J. Huang, “Atutorial on energy-based learning,” inPredicting Structured Data,MIT Press, 2006.
[60]J. Ngiam, Z. Chen, P. W. Koh, and A. Y. Ng, “Learning DeepEnergy Models,” inProceedings of ICML, pp. 1105–1112, 2011.
[61]A. van den Oord, N. Kalchbrenner, L. Espeholt, K. Kavukcuoglu,O. Vinyals, and A. Graves, “Conditional Image Generation withPixelCNN Decoders,” inProceedings of NeurIPS, vol. 29, pp. 4797–4805, 2016.
[62]L. Dinh, D. Krueger, and Y. Bengio, “NICE: Non-linear Indepen-dent Components Estimation,” inProceedings of ICLR, 2015.
[63]L. Dinh, J. Sohl-Dickstein, and S. Bengio, “Density estimationusing Real NVP,” inProceedings of ICLR, 2017.
[64]P. Vincent, “A Connection Between Score Matching and Denois-ing Autoencoders,”Neural Computation, vol. 23, pp. 1661–1674,2011.
[65]Y. Song, S. Garg, J. Shi, and S. Ermon, “Sliced Score Matching: AScalable Approach to Density and Score Estimation,” inProceed-ings of UAI, p. 204, 2019.
[66]B. D. Anderson, “Reverse-time diffusion equation models,”Stochastic Processes and their Applications, vol. 12, no. 3, pp. 313–326, 1982.
[67]T. Salimans, A. Karpathy, X. Chen, and D. P. Kingma, “Pix-elCNN++: Improving the PixelCNN with Discretized LogisticMixture Likelihood and Other Modifications,” inProceedings ofICLR, 2017.
[68]Q. Zhang and Y. Chen, “Diffusion normalizing flow,” inProceed-ings of NeurIPS, vol. 34, pp. 16280–16291, 2021.
[69]K. Swersky, M. Ranzato, D. Buchman, B. M. Marlin, and N. Fre-itas, “On Autoencoders and Score Matching for Energy BasedModels,” inProceedings of ICML, pp. 1201–1208, 2011.
[70]F. Bao, K. Xu, C. Li, L. Hong, J. Zhu, and B. Zhang, “Variational(gradient) estimate of the score function in energy-based latentvariable models,” inProceedings of ICML, pp. 651–661, 2021.
[71]T. Salimans, I. Goodfellow, W. Zaremba, V. Cheung, A. Radford,and X. Chen, “Improved techniques for training gans,” inPro-ceedings of NeurIPS, pp. 2234–2242, 2016.
[72]J. Austin, D. D. Johnson, J. Ho, D. Tarlow, and R. van den Berg,“Structured denoising diffusion models in discrete state-spaces,”inProceedings of NeurIPS, vol. 34, pp. 17981–17993, 2021.
[73]Y. Benny and L. Wolf, “Dynamic Dual-Output Diffusion Models,”inProceedings of CVPR, pp. 11482–11491, 2022.
[74]S. Bond-Taylor, P. Hessey, H. Sasaki, T. P. Breckon, and C. G.Willcocks, “Unleashing Transformers: Parallel Token Predictionwith Discrete Absorbing Diffusion for Fast High-Resolution Im-age Generation from Vector-Quantized Codes,” inProceedings ofECCV, 2022.
[75]J. Choi, J. Lee, C. Shin, S. Kim, H. Kim, and S. Yoon, “PerceptionPrioritized Training of Diffusion Models,” inProceedings of CVPR,pp. 11472–11481, 2022.
[76]V. De Bortoli, J. Thornton, J. Heng, and A. Doucet, “DiffusionSchr ?odinger bridge with applications to score-based generativemodeling,” inProceedings of NeurIPS, vol. 34, pp. 17695–17709,2021.
[77]J. Deasy, N. Simidjievski, and P. Li`o, “Heavy-tailed denoisingscore matching,”arXiv preprint arXiv:2112.09788, 2021.
[78]K. Deja, A. Kuzina, T. Trzci ?nski, and J. M. Tomczak, “On Ana-lyzing Generative and Denoising Capabilities of Diffusion-BasedDeep Generative Models,”arXiv preprint arXiv:2206.00070, 2022.
[79]A. Jolicoeur-Martineau, R. Pich ?e-Taillefer, I. Mitliagkas, and R. T.des Combes, “Adversarial score matching and improved sam-pling for image generation,” inProceedings of ICLR, 2021.
[80]A. Jolicoeur-Martineau, K. Li, R. Pich ?e-Taillefer, T. Kachman, andI. Mitliagkas, “Gotta go fast when generating data with score-based models,”arXiv preprint arXiv:2105.14080, 2021.
[81]D. Kim, B. Na, S. J. Kwon, D. Lee, W. Kang, and I.-C. Moon,“Maximum Likelihood Training of Implicit Nonlinear DiffusionModels,”arXiv preprint arXiv:2205.13699, 2022.
[82]D. Kingma, T. Salimans, B. Poole, and J. Ho, “Variational diffu-sion models,” inProceedings of NeurIPS, vol. 34, pp. 21696–21707,2021.
[83]Z. Kong and W. Ping, “On Fast Sampling of Diffusion Probabilis-tic Models,” inProceedings of INNF+, 2021.
[84]M. W. Lam, J. Wang, R. Huang, D. Su, and D. Yu, “Bilateral de-noising diffusion models,”arXiv preprint arXiv:2108.11514, 2021.
[85]L. Liu, Y. Ren, Z. Lin, and Z. Zhao, “Pseudo Numerical Methodsfor Diffusion Models on Manifolds,” inProceedings of ICLR, 2022.
[86]H. Ma, L. Zhang, X. Zhu, J. Zhang, and J. Feng, “AcceleratingScore-Based Generative Models for High-Resolution Image Syn-thesis,”arXiv preprint arXiv:2206.04029, 2022.
[87]E. Nachmani, R. S. Roman, and L. Wolf, “Non-Gaussian denois-ing diffusion models,”arXiv preprint arXiv:2106.07582, 2021.88]R. San-Roman, E. Nachmani, and L. Wolf, “Noise estimationfor generative diffusion models,”arXiv preprint arXiv:2104.02600,2021.
[89]V. Sehwag, C. Hazirbas, A. Gordo, F. Ozgenel, and C. Canton,“Generating High Fidelity Data from Low-density Regions usingDiffusion Models,” inProceedings of CVPR, pp. 11492–11501, 2022.
[90]G. Wang, Y. Jiao, Q. Xu, Y. Wang, and C. Yang, “Deep gener-ative learning via Schr ?odinger bridge,” inProceedings of ICML,pp. 10794–10804, 2021.
[91]Z. Wang, H. Zheng, P. He, W. Chen, and M. Zhou,“Diffusion-GAN: Training GANs with Diffusion,”arXiv preprintarXiv:2206.02262, 2022.
[92]D. Watson, J. Ho, M. Norouzi, and W. Chan, “Learning toefficiently sample from diffusion probabilistic models,”arXivpreprint arXiv:2106.03802, 2021.
[93]Z. Xiao, K. Kreis, and A. Vahdat, “Tackling the generative learn-ing trilemma with denoising diffusion GANs,” inProceedings ofICLR, 2022.
[94]H. Zheng, P. He, W. Chen, and M. Zhou, “Truncated diffusionprobabilistic models,”arXiv preprint arXiv:2202.09671, 2022.
[95]F. Bordes, R. Balestriero, and P. Vincent, “High fidelity visualiza-tion of what your self-supervised representation knows about,”Transactions on Machine Learning Research, 2022.
[96]A. Campbell, J. Benton, V. De Bortoli, T. Rainforth, G. Deligianni-dis, and A. Doucet, “A Continuous Time Framework for DiscreteDenoising Models,”arXiv preprint arXiv:2205.14987, 2022.
[97]C.-H. Chao, W.-F. Sun, B.-W. Cheng, Y.-C. Lo, C.-C. Chang,Y.-L. Liu, Y.-L. Chang, C.-P. Chen, and C.-Y. Lee, “DenoisingLikelihood Score Matching for Conditional Score-Based DataGeneration,” inProceedings of ICLR, 2022.
[98]J. Ho, C. Saharia, W. Chan, D. J. Fleet, M. Norouzi, and T. Sal-imans, “Cascaded Diffusion Models for High Fidelity ImageGeneration,”Journal of Machine Learning Research, vol. 23, no. 47,pp. 1–33, 2022.
[99]J. Ho and T. Salimans, “Classifier-Free Diffusion Guidance,” inProceedings of NeurIPS Workshop on DGMs and Applications, 2021.
[100] T. Karras, M. Aittala, T. Aila, and S. Laine, “Elucidating the De-sign Space of Diffusion-Based Generative Models,”arXiv preprintarXiv:2206.00364, 2022.
[101] X. Liu, D. H. Park, S. Azadi, G. Zhang, A. Chopikyan, Y. Hu,H. Shi, A. Rohrbach, and T. Darrell, “More control for free!Image synthesis with semantic diffusion guidance,”arXiv preprintarXiv:2112.05744, 2021.
[102] C. Lu, Y. Zhou, F. Bao, J. Chen, C. Li, and J. Zhu, “DPM-Solver:A Fast ODE Solver for Diffusion Probabilistic Model Sampling inAround 10 Steps,”arXiv preprint arXiv:2206.00927, 2022.
[103] T. Salimans and J. Ho, “Progressive distillation for fast samplingof diffusion models,” inProceedings of ICLR, 2022.
[104] V. Singh, S. Jandial, A. Chopra, S. Ramesh, B. Krishnamurthy,and V. N. Balasubramanian, “On Conditioning the Input Noisefor Controlled Image Generation with Diffusion Models,”arXivpreprint arXiv:2205.03859, 2022.
[105] S. Gu, D. Chen, J. Bao, F. Wen, B. Zhang, D. Chen, L. Yuan,and B. Guo, “Vector quantized diffusion model for text-to-imagesynthesis,” inProceedings of CVPR, pp. 10696–10706, 2022.
[106] A. Ramesh, P. Dhariwal, A. Nichol, C. Chu, and M. Chen, “Hi-erarchical text-conditional image generation with CLIP latents,”arXiv preprint arXiv:2204.06125, 2022.
[107] C. Saharia, W. Chan, S. Saxena, L. Li, J. Whang, E. Denton,S. K. S. Ghasemipour, B. K. Ayan, S. S. Mahdavi, R. G. Lopes,et al., “Photorealistic Text-to-Image Diffusion Models with DeepLanguage Understanding,”arXiv preprint arXiv:2205.11487, 2022.
[108] Q. Zhang and Y. Chen, “Fast Sampling of Diffusion Models withExponential Integrator,”arXiv preprint arXiv:2204.13902, 2022.
[109] O. Avrahami, O. Fried, and D. Lischinski, “Blended latent diffu-sion,”arXiv preprint arXiv:2206.02779, 2022.
[110] H. Sasaki, C. G. Willcocks, and T. P. Breckon, “UNIT-DDPM: UN-paired Image Translation with Denoising Diffusion ProbabilisticModels,”arXiv preprint arXiv:2104.05358, 2021.
[111] G. Batzolis, J. Stanczuk, C.-B. Sch ?onlieb, and C. Etmann, “Non-Uniform Diffusion Models,”arXiv preprint arXiv:2207.09786,2022.
[112] A. Blattmann, R. Rombach, K. Oktay, and B. Ommer, “Retrieval-Augmented Diffusion Models,”arXiv preprint arXiv:2204.11824,2022.
[113] R. Gao, Y. Song, B. Poole, Y. N. Wu, and D. P. Kingma, “LearningEnergy-Based Models by Diffusion Recovery Likelihood,” inProceedings of ICLR, 2021.
[114] M. Hu, Y. Wang, T.-J. Cham, J. Yang, and P. N. Suganthan, “GlobalContext with Discrete Diffusion in Vector Quantised Modellingfor Image Generation,” inProceedings of CVPR, pp. 11502–11511,2022.
[115] V. Khrulkov and I. Oseledets, “Understanding DDPM La-tentCodesThroughOptimalTransport,”arXivpreprintarXiv:2202.07477, 2022.
[116] G. Kim, T. Kwon, and J. C. Ye, “DiffusionCLIP: Text-GuidedDiffusion Models for Robust Image Manipulation,” inProceedingsof CVPR, pp. 2426–2435, 2022.
[117] S. Luo and W. Hu, “Diffusion probabilistic models for 3D pointcloud generation,” inProceedings of CVPR, pp. 2837–2845, 2021.
[118] Z. Lyu, X. Xu, C. Yang, D. Lin, and B. Dai, “Accelerating DiffusionModels via Early Stop of the Diffusion Process,”arXiv preprintarXiv:2205.12524, 2022.
[119] K. Preechakul, N. Chatthee, S. Wizadwongsa, and S. Suwa-janakorn, “Diffusion Autoencoders: Toward a Meaningful andDecodable Representation,” inProceedings of CVPR, pp. 10619–10629, 2022.
[120] Y. Shi, V. De Bortoli, G. Deligiannidis, and A. Doucet, “Con-ditional Simulation Using Diffusion Schr ?odinger Bridges,” inProceedings of UAI, 2022.
[121] D. Hu, Y. K. Tao, and I. Oguz, “Unsupervised denoising of retinalOCT with diffusion probabilistic model,” inProceedings of SPIEMedical Imaging, vol. 12032, pp. 25–34, 2022.
[122] H. Chung and J. C. Ye, “Score-based diffusion models for accel-erated MRI,”Medical Image Analysis, vol. 80, p. 102479, 2022.
[123] M. ?Ozbey, S. U. Dar, H. A. Bedel, O. Dalmaz, S ? . ?Ozturk,A. G ?ung ?or, and T. C ? ukur, “Unsupervised Medical ImageTranslation with Adversarial Diffusion Models,”arXiv preprintarXiv:2207.08208, 2022.
[124] Y. Song, L. Shen, L. Xing, and S. Ermon, “Solving inverse prob-lems in medical imaging with score-based generative models,” inProceedings of ICLR, 2022.
[125] W. Harvey, S. Naderiparizi, V. Masrani, C. Weilbach, and F. Wood,“Flexible Diffusion Modeling of Long Videos,”arXiv preprintarXiv:2205.11495, 2022.
[126] J. Ho, T. Salimans, A. A. Gritsenko, W. Chan, M. Norouzi, andD. J. Fleet, “Video diffusion models,” inProceedings of DGM4HSD,2022.
[127] R. Yang, P. Srivastava, and S. Mandt, “Diffusion ProbabilisticModeling for Video Generation,”arXiv preprint arXiv:2203.09481,2022.
[128] T. H ?oppe, A. Mehrjou, S. Bauer, D. Nielsen, and A. Dittadi,“Diffusion Models for Video Prediction and Infilling,”arXivpreprint arXiv:2206.07696, 2022.
[129] G. Giannone, D. Nielsen, and O. Winther, “Few-Shot DiffusionModels,”arXiv preprint arXiv:2205.15463, 2022.
[130] G. Jeanneret, L. Simon, and F. Jurie, “Diffusion Models for Coun-terfactual Explanations,”arXiv preprint arXiv:2203.15636, 2022.
[131] O. ?Ozdenizci and R. Legenstein, “Restoring Vision in AdverseWeather Conditions with Patch-Based Denoising Diffusion Mod-els,”arXiv preprint arXiv:2207.14626, 2022.
[132] B. Kim, I. Han, and J. C. Ye, “DiffuseMorph: Unsupervised De-formable Image Registration Along Continuous Trajectory UsingDiffusion Models,”arXiv preprint arXiv:2112.05149, 2021.
[133] W. Nie, B. Guo, Y. Huang, C. Xiao, A. Vahdat, and A. Anandku-mar, “Diffusion models for adversarial purification,” inProceed-ings of ICML, 2022.
[134] W. Wang, J. Bao, W. Zhou, D. Chen, D. Chen, L. Yuan, and H. Li,“Semantic image synthesis via diffusion models,”arXiv preprintarXiv:2207.00050, 2022.
[135] L. Zhou, Y. Du, and J. Wu, “3D shape generation and completionthrough point-voxel diffusion,” inProceedings of ICCV, pp. 5826–5835, 2021.
[136] A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N.Gomez, ?. Kaiser, and I. Polosukhin, “Attention is all you need,”inProceedings of NIPS, vol. 30, pp. 6000–6010, 2017.
[137] M. Shannon, B. Poole, S. Mariooryad, T. Bagby, E. Batten-berg, D. Kao, D. Stanton, and R. Skerry-Ryan, “Non-saturatingGAN training as divergence minimization,”arXiv preprintarXiv:2010.08029, 2020.
[138] M. Arjovsky and L. Bottou, “Towards principled methods fortraining generative adversarial networks,” inProceedings of ICLR,2017.
[139] C. K. S?nderby, J. Caballero, L. Theis, W. Shi, and F. Husz ?ar,“Amortised map inference for image super-resolution,” inPro-ceedings of ICLR, 2017.
[140] H. Tachibana, M. Go, M. Inahara, Y. Katayama, and Y. Watan-abe, “It?o-Taylor Sampling Scheme for Denoising DiffusionProbabilistic Models using Ideal Derivatives,”arXiv preprintarXiv:2112.13339, 2021.
[141] J. Geiping, H. Bauermeister, H. Dr ?oge, and M. Moeller, “Invertinggradients – How easy is it to break privacy in federated learn-ing?,” inProceedings of NeurIPS, vol. 33, pp. 16937–16947, 2020.
[142] A. Radford, J. W. Kim, C. Hallacy, A. Ramesh, G. Goh, S. Agar-wal, G. Sastry, A. Askell, P. Mishkin, J. Clark, G. Krueger, andI. Sutskever, “Learning transferable visual models from naturallanguage supervision,” inProceedings of ICML, vol. 139, pp. 8748–8763, 2021.
[143] A. Van Den Oord, O. Vinyals, and K. Kavukcuoglu, “Neuraldiscrete representation learning,”Proceedings of NIPS, vol. 30,pp. 6309–6318, 2017.
[144] N. Reimers and I. Gurevych, “Sentence-BERT: Sentence Embed-dings using Siamese BERT-Networks,” inProceedings of EMNLP,pp. 3982–3992, 2019.
[145] J.-Y. Zhu, T. Park, P. Isola, and A. A. Efros, “Unpaired image-to-image translation using cycle-consistent adversarial networks,”inProceedings of ICCV, pp. 2223–2232, 2017.
[146] P. Esser, R. Rombach, and B. Ommer, “Taming transformersfor high-resolution image synthesis,” inProceedings of CVPR,pp. 12873–12883, 2021.
[147] X. Wang, K. Yu, S. Wu, J. Gu, Y. Liu, C. Dong, Y. Qiao, andC. Change Loy, “ESRGAN: Enhanced Super-Resolution Genera-tive Adversarial Networks,” inProceedings of ECCVW, pp. 63–79,2018.
[148] G. Lin, A. Milan, C. Shen, and I. Reid, “RefineNet: Multi-PathRefinement Networks for High-Resolution Semantic Segmenta-tion,” inProceeding of CVPR, pp. 5168–5177, 2017.
[149] N. Kovachki, R. Baptista, B. Hosseini, and Y. Marzouk,“Conditional sampling with monotone GANs,”arXiv preprintarXiv:2006.06755, 2020.
[150] Y. Marzouk, T. Moselhy, M. Parno, and A. Spantini, “Samplingvia Measure Transport: An Introduction,” inHandbook of Uncer-tainty Quantification, (Cham), pp. 1–41, Springer, 2016.
[151] S. Borgeaud, A. Mensch, J. Hoffmann, T. Cai, E. Rutherford,K. Millican, G. B. Van Den Driessche, J.-B. Lespiau, B. Damoc,A. Clark, D. De Las Casas, A. Guy, J. Menick, R. Ring, T. Hen-nigan, S. Huang, L. Maggiore, C. Jones, A. Cassirer, A. Brock,M. Paganini, G. Irving, O. Vinyals, S. Osindero, K. Simonyan,J. Rae, E. Elsen, and L. Sifre, “Improving Language Models byRetrieving from Trillions of Tokens,” inProceedings of ICML,vol. 162, pp. 2206–2240, 2022.
[152] I. Oguz, J. D. Malone, Y. Atay, and Y. K. Tao, “Self-fusion forOCT noise reduction,” inProceedings of SPIE Medical Imaging,vol. 11313, p. 113130C, SPIE, 2020.
[153] R. T. Ionescu, F. S. Khan, M.-I. Georgescu, and L. Shao, “Object-Centric Auto-Encoders and Dummy Anomalies for AbnormalEvent Detection in Video,” inProceedings of CVPR, pp. 7842–7851,2019.
[154] ?O. C ? ic ?ek, A. Abdulkadir, S. S. Lienkamp, T. Brox, and O. Ron-neberger, “3D U-Net: Learning Dense Volumetric Segmentationfrom Sparse Annotation,” inProceedings of MICCAI, pp. 424–432,2016.
[155] R. Q. Charles, H. Su, M. Kaichun, and L. J. Guibas, “PointNet:Deep Learning on Point Sets for 3D Classification and Segmenta-tion,” inProceedings of CVPR, pp. 77–85, 2017.
[156] G. Balakrishnan, A. Zhao, M. R. Sabuncu, J. Guttag, and A. V.Dalca, “An unsupervised learning model for deformable medicalimage registration,” inProceedings of CVPR, pp. 9252–9260, 2018.
[157] X. Li, T.-K. L. Wong, R. T. Chen, and D. Duvenaud, “Scalablegradients for stochastic differential equations,” inProceedings ofAISTATS, pp. 3870–3882, 2020.
[158] T. Park, M.-Y. Liu, T.-C. Wang, and J.-Y. Zhu, “Semantic imagesynthesis with spatially-adaptive normalization,” inProceedingsof CVPR, pp. 2337–2346, 2019.
[159] B. Kawar, G. Vaksman, and M. Elad, “Snips: Solving noisy in-verse problems stochastically,” inProceedings of NeurIPS, vol. 34,pp. 21757–21769, 2021