[人工智能]LIFELONG LEARNING WITH DYNAMICALLY EXPANDABLE NETWORKS论文阅读+代码解析

论文地址点这里
本篇论文来自2018年ICML上的一篇论文。

一. 介绍

终身学习(持续学习)，即任务按顺序到达的持续学习问题，是迁移学习中的一个重要主题。终身学习的主要目标是利用早期任务中的知识，以获得更好的性能，或加快后期任务模型的收敛速度。虽然有许多不同的方法来解决这个问题，但我们考虑在深度学习下的终身学习，以利用深度神经网络的能力。幸运的是，对于深度学习，可以通过学习的网络权重直接存储和传输知识。学习的权重可以作为现有任务的知识，而新任务可以通过简单地共享这些权重来利用这些知识。
本文提出了一种新的深度网络模型以及一种高效的增量学习算法，称之为动态可扩展网络（DEN）。在终身学习场景中，DEN最大限度地利用在所有先前任务中学习到的网络，有效地学习预测新任务，同时在必要时通过添加或拆分神经元来动态增加网络容量。我们的方法适用于任何一般的深网络，包括卷积网络。

二. 动态可扩展网络的增量学习

我们考虑终身学习场景下深度神经网络的增量训练问题，其中训练数据分布未知的未知任务数依次到达模型。具体来说，有一个任务序列$T$，$t=1,...,t,...,T$，每个任务在不同的时间点$t$到来，其对应着数据集 D t = { x i , y i } i = 1 N t \mathcal{D}_t=\{x_i,y_i\}^{N_t}_{i=1} Dt?={xi?,yi?}i=1Nt??。终身学习环境下，所有值钱的训练数据都不可用，具体来说，在时刻$t$时终身学习通过解决一下问题来学习模型参数$W_t$：
$$\underset{{\mathbf{W}}^t}{\mathrm{minimize}}\mathcal{L}\left({\mathbf{W}}^t;{\mathbf{W}}^{t?1},{\mathcal{D}}_t\right)+\lambda \Omega \left({\mathbf{W}}^t\right),t=1,\dots$$
其中$\mathcal{L}$表示为特定的损失函数，$W^t$表示为任务$t$的参数，$\Omega (W^t)$表示为正则化的公式，使得参数不会过度漂移。在这里，我们假设神经网络 W t = { W l } l = 1 L W^t=\{W_l\}^L_{l=1} Wt={Wl?}l=1L?。为了应对终身学习的这些挑战，我们让网络最大限度地利用从以前的任务中获得的知识，同时允许网络在积累的知识不能充分解释新任务时动态扩展其能力。下面的算法和图描述了我们的增量学习过程。


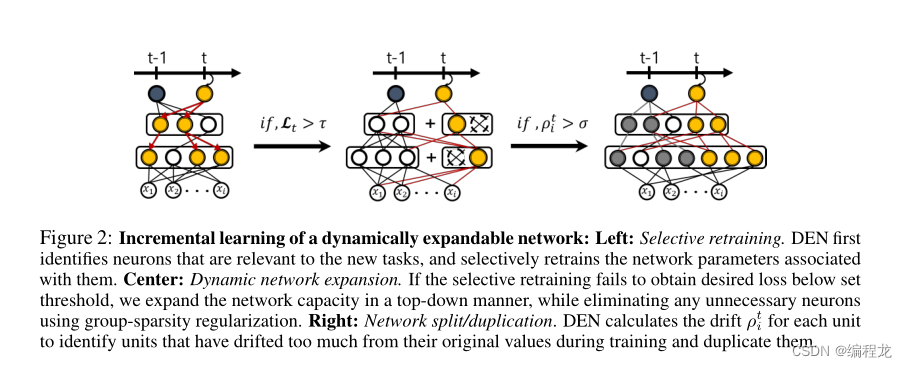
选择性地重新训练： 为一系列任务训练模型的最简单方法是每次新任务到来时重新训练整个模型。然而，这样的再培训对于深度神经网络来说将是非常昂贵的。因此，本文只对接受新任务影响的权重进行再培训。为了达到这样的效果，我们首先使用l1正则化训练模型，以提高权重的稀疏性，从而使得每个神经元连接下层中的少数神经元：
$$\underset{{\mathbf{W}}^{t=1}}{\mathrm{minimize}}\mathcal{L}\left({\mathbf{W}}^{t=1};{\mathcal{D}}_t\right)+\mu \sum _{l=1}^L{\Vert {\mathbf{W}}_l^{t=1}\Vert }_1$$
其中$1\le l\le L$表示为第$l$层的网络, $\mu$表示为正则化的超参数。
在整个增量学习过程中，保持$W^{t?1}$是稀疏的，这就能够专注于子网连接的新任务，从而大大减少计算开销。为此，当一个新任务$t$到达模型时，我们首先拟合一个稀疏线性模型，通过解决以下问题，使用神经网络的最顶层隐藏单元预测任务$t$：
$$\underset{{\mathbf{W}}_{L,t}^t}{\mathrm{minimize}}\mathcal{L}\left({\mathbf{W}}_{L,t}^t;{\mathbf{W}}_{1:L?1}^{t?1},{\mathcal{D}}_t\right)+\mu {\Vert {\mathbf{W}}_{L,t}^t\Vert }_1$$
这里${\mathbf{W}}_{1:L?1}^{t?1}$表示整个参数除了${\mathbf{W}}_{L,t}^t$，这也就是说，此公式只是优化了最后一个隐藏层和$o_t$。一旦在此层建立稀疏连接就可以识别网络中受训练影响的所有单位和权重，同时保持网络中未连接的部分不变。具体来说，从那些选定的节点开始，在网络上执行广度优先搜索，以识别所有具有$o_t$路径的单元（和输入特征）。然后，只训练选定子网络S的权重，表示为$W_S^t$：
$$\underset{{\mathbf{W}}_S^t}{\mathrm{minimize}}\mathcal{L}\left({\mathbf{W}}_S^t;{\mathbf{W}}_{S^c}^{t?1},{\mathcal{D}}_t\right)+\mu {\Vert {\mathbf{W}}_S^t\Vert }_2$$
由于稀疏的连接已经建立，直接食用l2正则再次降低训练开销，下面描述了算法的过程：

动态网络扩展： 如果新任务与旧任务高度相关，或者从每个任务中获得的部分知识汇总足以解释新任务，则仅进行选择性再培训就足以完成新任务。然而，当学习到的特征不能准确地表示新任务时，需要向网络中引入额外的神经元，以说明新任务所需的特征。为了克服这些限制，我们提出了一种有效的方法，即使用组稀疏正则化来动态决定在哪一层为每个任务添加多少神经元，而无需对每个单元的网络进行重复再训练。假设我们扩展了第l层的网络（扩展量为一个常数，假设为$k$）那就包括了两个部分：${\mathbf{W}}_l^t=\left[{\mathbf{W}}_l^{t?1};{\mathbf{W}}_l^{\mathcal{N}}\right]$以及${\mathbf{W}}_{l?1}^t=\left[{\mathbf{W}}_{l?1}^{t?1};{\mathbf{W}}_{l?1}^{\mathcal{N}}\right]$，其中${\mathbf{W}}_l^{\mathcal{N}}$表示为扩展的参数。由于我们并不总是希望添加所有k个单员（取决于新任务和旧任务之间的相关性），因此我们对添加的参数执行组稀疏性正则化，如下所示：
$$\underset{{\mathbf{W}}_l^{\mathcal{N}}}{\mathrm{minimize}}\mathcal{L}\left({\mathbf{W}}_l^{\mathcal{N}};{\mathbf{W}}_l^{t?1},{\mathcal{D}}_t\right)+\mu {\Vert {\mathbf{W}}_l^{\mathcal{N}}\Vert }_1+\gamma \sum _g{\Vert {\mathbf{W}}_{l,g}^{\mathcal{N}}\Vert }_2$$
选择性再训练完成后，网络会检查损失是否低于特定阈值。如果不是，那么在每一层，我们用k个神经元扩展其容量，并求解上面等式。由于等式中的群稀疏正则化，被认为是训练中不必要的隐藏单元（或卷积）将被完全删除。下面是算法的过程：

网络拆分/复制： 终身学习中的一个关键挑战是语义偏移问题，即灾难性遗忘，它描述了模型逐渐适应后来学习的任务的问题，从而忘记了它为早期任务所学的内容，从而导致它们的性能退化。防止语义漂移的最流行但最简单的方法是使用l2-正则化将参数正则化，使其不会偏离其原始值太多，如下所示：
$$\underset{{\mathbf{W}}^t}{\mathrm{minimize}}\mathcal{L}\left({\mathbf{W}}^t;{\mathcal{D}}_t\right)+\lambda {\Vert {\mathbf{W}}^t?{\mathbf{W}}^{t?1}\Vert }_2^2$$
其中$\lambda$为正则化的超参数。虽然使用这种方法可以有效缓解参数偏移情况，但依旧很难平衡好这个尺度。
最好的方式是分割神经元，这样就有两个任务的最佳特征。在执行了上述的等式之后，可以测量每一个神经元的偏移量：${\rho }_i^t$，然后根据偏移量来确定是否裂解这些神经元，给新分裂的神经元两份参数（旧任务和新任务），具体算法如下：

三. 代码解析

本文的官方代码在这里：添加链接描述，是按照tensorflow写的，本次我参考的是另一个人在github投稿的pytorch代码，点击这里（遗憾的是他的代码有残缺，一些地方没写完，之后有空我把它补齐）

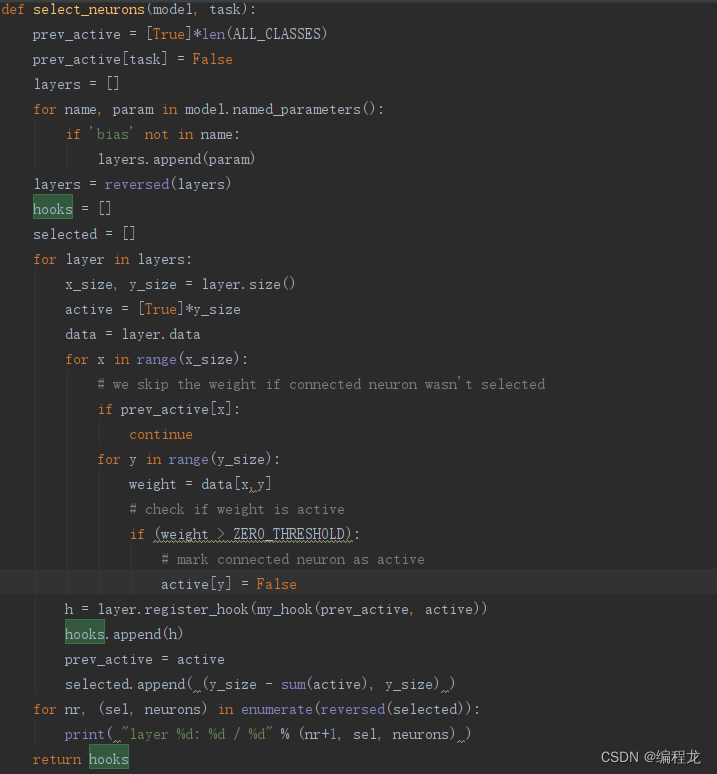
这里展示的是选择重新训练的神经元，在新任务到来后，先对最后一层参数稀疏处理然后依次从最后一层选择不为0的（大于1e-4），然后再往前推，这里的hook是存了个掩码，主要是方便控制求导的内容。