1.简介
通道注意力在计算机视觉领域取得了重大成功,许多工作都致力于设计更加高效的通道注意力模块,而忽略了一个问题,使用全局平均池化作为预处理。
基于频率分析,本文从数学上证明了全局平均池化是频域特征分解的特例。在此基础上,推广了频域中的通道注意力预处理机制,并提出了全新的多谱通道注意力的FcaNet。
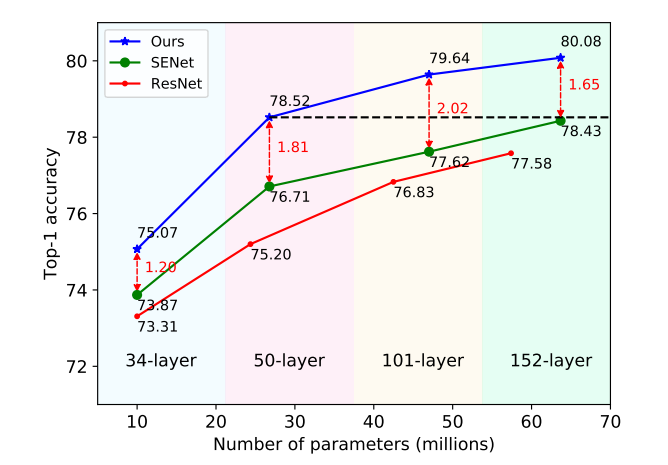
只需改变原始SENet??中的一行代码,在图像分类、目标检测和实例分割任务上与其他信道关注方法相比取得了最先进的结果。所提出方法与基线SENet?50 相比,在参数数量和计算成本相同的情况下,在ImageNet? 上的Top?1 精度可以提高1.8%
传统的通道注意方法致力于构建各种通道重要性权重函数,这种权重函数要求每个通道都有一个标量来进行计算,由于计算开销有限,简单有效的全局平均池化(G A P GAPGAP)成为了他们的不二之选。
但是一个潜在的问题是G A P GAPGAP?是否能够捕获丰富的输入信息,也就是说,仅仅平均值是否足够表示通道注意力中的各个通道。
因此做了以下分析:
1)不同的通道可能拥有相同的平均值,而其代表的语义信息是不相同的;
2)从频率分析的角度,可以证明GAP等价于DCT??的最低频率,仅仅使用GAP相当于丢弃了其他许多包含着通道特征的信息;
3)CBAM还表示,仅使用GAP是不够的,因此额外引入了GMP?。?
分析了GAP的有效性和不足之后,根据DCT提出了FcaNet。?
2.DCT(离散余弦变换)
DCT,即离散余弦变换,常用图像压缩算法,步骤如下
1)分割,首先将图像分割成8x8或16x16的小块;
2)DCT变换,对每个小块进行DCT变换;
3)舍弃高频系数(AC系数),保留低频信息(DC系数)。高频系数一般保存的是图像的边界、纹理信息,低频信息主要是保存的图像中平坦区域信息。
4)图像的低频和高频,高频区域指的是空域图像中突变程度大的区域(比如目标边界区域),通常的纹理丰富区域。
二维DCT变换就是将二维图像从空间域转换到频率域。形象的说,就是计算出图像由哪些二维余弦波构成,其主要用于数据或图像的压缩,能够将空间域的信号转换到频域上,具有良好的去相关性的性能。二维的DTC??公式如下:
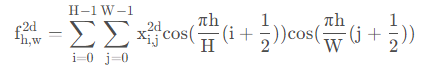
二维的逆DTC公式如下:
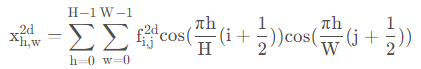
我们称二者的共有项为基函数:
![]()
当h、w都为0时,就等价于GAP
根据公式????我们可以知道特征可以被分解为不同频率分量的组合,自然而然地,可以将其在通道注意力上进行推广——使用多个频率分量。
2.1 分块进行DCT变换
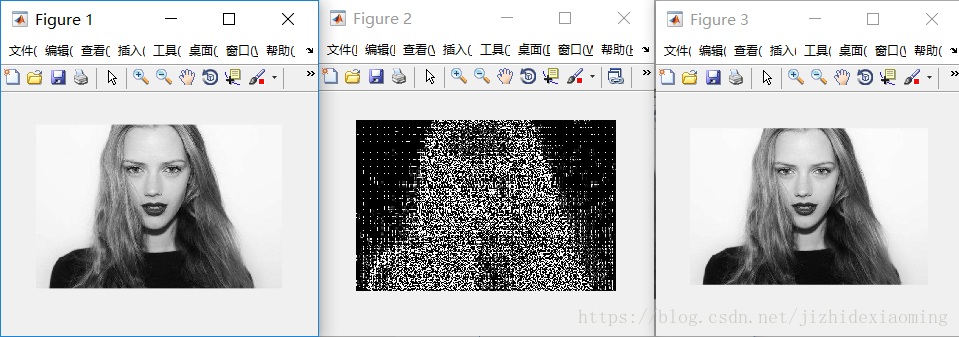
效果图,分别是原图,所有dct系数小块组成图,反dct变换回来的图:
?将图像分成8x8的小块,对每个小块依次进行dct变换,反变换回来时,也是依次处理每个小块。
放大后的dct系数块组成的图像:
1)发现每个小块的左上角,即一个DC系数,最亮,保存的是原图像低频信息,反应的是空域图像中平坦区域的信息;
2)小块的其他地方,即63个AC系数,保存的是高频信息,反应的是空域图像中的突变区域的信息;
3)对整个图像而言,背景区域是平坦区域,没有纹理信息,所以AC系数很小,而代表亮度信息的DC系数很大;
4)头发区域不仅含有亮度信息,纹理信息也丰富,所以AC系数值很大。
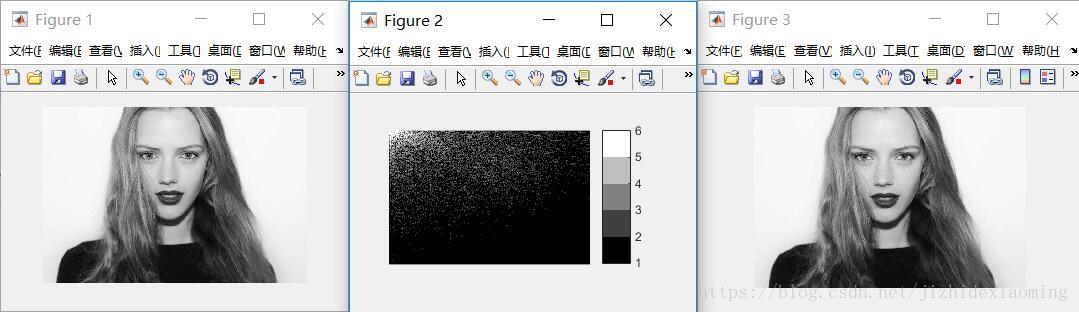
2.2 对整个图像进行DCT变换
?效果图,分别是原图、整个图像变换后系数图、反变换得到的图:
3.Multi-Spectral Attention Module
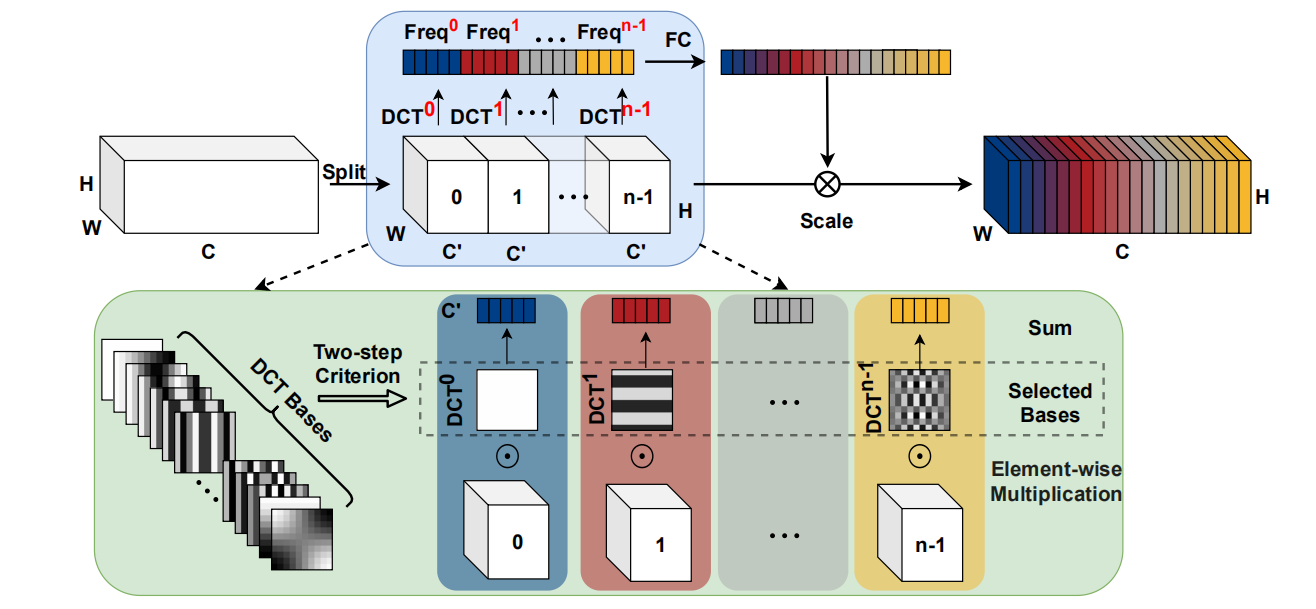
主要分为以下两个步骤:
将输入分组,选取不同频率分量
与SENet????两层的MLP得到通道注意力权重
并且只要修改一行代码就可以实现:
?4.Fcanet代码
# c2wh为生成的字典,字典名为输入Fca模块的通道数,字典值为通道数对应的输入特征图大小
c2wh = dict([(16,112),(64,112),(72,56),(120,28),(240,28),(200,14),(184,14),(480,14),(672,14),(960,7)])
# input_c为输入通道数
self.att = MultiSpectralAttentionLayer(input_c, c2wh[input_c], c2wh[input_c], reduction=reduction, freq_sel_method = 'top16')如何获得DCT权重
首先获得选取的频率分量的“坐标”:
import math
import torch
import torch.nn as nn
def get_freq_indices(method):
# 获得分量排名的坐标
assert method in ['top1', 'top2', 'top4', 'top8', 'top16', 'top32',
'bot1', 'bot2', 'bot4', 'bot8', 'bot16', 'bot32',
'low1', 'low2', 'low4', 'low8', 'low16', 'low32']
num_freq = int(method[3:])
if 'top' in method:
all_top_indices_x = [0, 0, 6, 0, 0, 1, 1, 4, 5, 1, 3, 0, 0, 0, 3, 2, 4, 6, 3, 5, 5, 2, 6, 5, 5, 3, 3, 4, 2, 2,
6, 1]
all_top_indices_y = [0, 1, 0, 5, 2, 0, 2, 0, 0, 6, 0, 4, 6, 3, 5, 2, 6, 3, 3, 3, 5, 1, 1, 2, 4, 2, 1, 1, 3, 0,
5, 3]
mapper_x = all_top_indices_x[:num_freq]
mapper_y = all_top_indices_y[:num_freq]
elif 'low' in method:
all_low_indices_x = [0, 0, 1, 1, 0, 2, 2, 1, 2, 0, 3, 4, 0, 1, 3, 0, 1, 2, 3, 4, 5, 0, 1, 2, 3, 4, 5, 6, 1, 2,
3, 4]
all_low_indices_y = [0, 1, 0, 1, 2, 0, 1, 2, 2, 3, 0, 0, 4, 3, 1, 5, 4, 3, 2, 1, 0, 6, 5, 4, 3, 2, 1, 0, 6, 5,
4, 3]
mapper_x = all_low_indices_x[:num_freq]
mapper_y = all_low_indices_y[:num_freq]
elif 'bot' in method:
all_bot_indices_x = [6, 1, 3, 3, 2, 4, 1, 2, 4, 4, 5, 1, 4, 6, 2, 5, 6, 1, 6, 2, 2, 4, 3, 3, 5, 5, 6, 2, 5, 5,
3, 6]
all_bot_indices_y = [6, 4, 4, 6, 6, 3, 1, 4, 4, 5, 6, 5, 2, 2, 5, 1, 4, 3, 5, 0, 3, 1, 1, 2, 4, 2, 1, 1, 5, 3,
3, 3]
mapper_x = all_bot_indices_x[:num_freq]
mapper_y = all_bot_indices_y[:num_freq]
else:
raise NotImplementedError
return mapper_x, mapper_y
class MultiSpectralAttentionLayer(torch.nn.Module):
def __init__(self, channel, dct_h, dct_w, reduction=16, freq_sel_method='top16'):
# c2wh = dict([(64,56), (128,28), (256,14) ,(512,7)])
# dct_h = c2wh[planes], dct_w = c2wh[planes]
super(MultiSpectralAttentionLayer, self).__init__()
self.reduction = reduction
self.dct_h = dct_h
self.dct_w = dct_w
# mapper_x = [0,0,6,0,0,1,1,4,5,1,3,0,0,0,3,2]
# mapper_y = [0,1,0,5,2,0,2,0,0,6,0,4,6,3,5,2]
mapper_x, mapper_y = get_freq_indices(freq_sel_method)
self.num_split = len(mapper_x) # 16
mapper_x = [temp_x * (dct_h // 7) for temp_x in mapper_x]
mapper_y = [temp_y * (dct_w // 7) for temp_y in mapper_y]
# make the frequencies in different sizes are identical to a 7x7 frequency space
# eg, (2,2) in 14x14 is identical to (1,1) in 7x7
self.dct_layer = MultiSpectralDCTLayer(dct_h, dct_w, mapper_x, mapper_y, channel)
self.fc = nn.Sequential(
nn.Linear(channel, channel // reduction, bias=False),
nn.ReLU(inplace=True),
nn.Linear(channel // reduction, channel, bias=False),
nn.Sigmoid()
)
def forward(self, x):
n, c, h, w = x.shape
x_pooled = x
if h != self.dct_h or w != self.dct_w:
x_pooled = torch.nn.functional.adaptive_avg_pool2d(x, (self.dct_h, self.dct_w))
# If you have concerns about one-line-change, don't worry. :)
# In the ImageNet models, this line will never be triggered.
# This is for compatibility in instance segmentation and object detection.
y = self.dct_layer(x_pooled)
y = self.fc(y).view(n, c, 1, 1)
return x * y.expand_as(x)
class MultiSpectralDCTLayer(nn.Module):
"""
Generate dct filters
"""
def __init__(self, height, width, mapper_x, mapper_y, channel):
super(MultiSpectralDCTLayer, self).__init__()
assert len(mapper_x) == len(mapper_y)
# assert channel % len(mapper_x) == 0
self.num_freq = len(mapper_x)
# fixed DCT init
# 对应于公式中的H,W,i,j,C
self.register_buffer('weight', self.get_dct_filter(height, width, mapper_x, mapper_y, channel))
# fixed random init
# self.register_buffer('weight', torch.rand(channel, height, width))
# learnable DCT init
# self.register_parameter('weight', self.get_dct_filter(height, width, mapper_x, mapper_y, channel))
# learnable random init
# self.register_parameter('weight', torch.rand(channel, height, width))
# num_freq, h, w
def forward(self, x):
assert len(x.shape) == 4, 'x must been 4 dimensions, but got ' + str(len(x.shape))
# n, c, h, w = x.shape
print(x.shape) # [24, 72, 56, 56]
print(self.weight.shape) # [288, 56, 56]
x = x * self.weight
result = torch.sum(x, dim=[2, 3]) # 在空间维度上求和
return result
def build_filter(self, pos, freq, POS): # 对应i/j, h/w, H/W
result = math.cos(math.pi * freq * (pos + 0.5) / POS) / math.sqrt(POS) # 基函数公式的一半
if freq == 0:
# 对应gap的形式
return result
else:
return result * math.sqrt(2)
def get_dct_filter(self, tile_size_x, tile_size_y, mapper_x, mapper_y, channel):
dct_filter = torch.zeros(channel, tile_size_x, tile_size_y) # 对于每一个BATCH都是相同的
# c_part = channel // len(mapper_x) # 每一份的通道长度
c_part = 1
for i, (u_x, v_y) in enumerate(zip(mapper_x, mapper_y)):
for t_x in range(tile_size_x):
for t_y in range(tile_size_y):
dct_filter[i * c_part: (i + 1) * c_part, t_x, t_y] = self.build_filter(t_x, u_x,tile_size_x) * self.build_filter(t_y, v_y, tile_size_y)
# dct_filter[i: (i + 1), t_x, t_y] = self.build_filter(t_x, u_x,tile_size_x) * self.build_filter(t_y, v_y, tile_size_y)
return dct_filter