文章发表于2016年

文章链接:
1、概述
随着深度网络在目标检测领域的发展,网络的性能和准确率都在不断提升。但是存在的一个问题,深度网络很容易被一些图片(在人类看来没有意义)所欺骗,即使我们觉得该图像并不属于某一类别,但是深度网络还是会以高置信度将其分为该类。究其原因,这是因为我们训练网络时,使用的是封闭的数据集(有多少类别已经提前规定好,所以深度网络的选择只会在这些特定类别中去选择)。
作者在此强调更多的应该是:模型应该拒绝未知类,而不是以高置信度将其辨认为已知类。
但是在现实世界中,大多数检测任务都是开放的,在动态和不断变化的现实世界中部署识别系统时,绝大多数的识别系统是为静态封闭世界设计的,其中主要的假设是所有类别都是已知的。深度网络,就像许多经典的机器学习工具一样,被设计用于执行封闭集识别。作者认为深度网络应该具有识别已知类和未知类的能力。因此作者提出了一种新的方法–用于使深度网络识别开放数据集,通过引入一个新的模型层–OpenMax,它可以估计一个输入来自未知类的概率。而估计未知类的一个关键就是将元识别(Meta-Recognition)概念应用于网络倒数第二层的激活模式。基于此方法,深度网络可以拒绝欺骗性的图片以及与系统不相关的图像集。OpenMax大大减少了由深度网络造成的明显错误的数量。证明了OpenMax概念提供了有界开空间风险,从而正式提供了一个开集识别解决方案。
总结:
(1)当前的模型存在错误识别问题,无法处理开放数据集
(2)提出了openmax方法,可以使模型拒绝欺骗类以及不相关类图像,从而降低错误率
(3)与OWOD论文相比,该论文没有解决怎么识别新类的问题。
2、当前待解决的问题(2016年)
--------为何深度网络识别开放数据仍然是一个待解决的问题?
主要的问题出在了softmax层上,在大多数网络中,最后一层全连接层的输出被输入到softmax层中,从而在N个已知类别中产生一个概率分布,这就造成了在给定一个未知类作为输入时,网络总会找到一个最有可能的已知类。而在实际中,人们希望假设输入为未知类,那么输出的所有已知类概率都很低,这样可以通过一个阈值来拒绝这个未知类。同时因为softmax层的封闭性,网络没办法增量学习新的类别。如果单独训练新类别,还会造成遗忘问题。
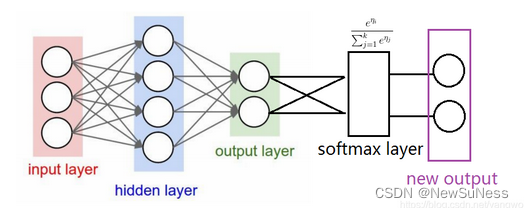
3、本论文的创新点—OpenMax层(扩展softmax层使其可以预测未知类别)
通过扩展softmax层,使其可以预测给定输入属于未知类的可能性。同时,将元学习的概念加入深度网络中,使用网络倒数第二层(Softmax层前面的全连接层)的分数来评估当前的输入是否远离已知类别。该层的分数称为–激活向量(activation vector(AV))。
主要贡献:
*利用激活向量的多类元识别来估计深度网络故障的概率
*利用元识别和OpenMax形成开放集深度网络,并证明了所提出的方法可以管理深度网络的开放空间风险
*开放集深度网络在保持测试图像准确性的同时,拒绝未知类、欺骗图像、对抗图像明显错误的有效性
4、关于activation vector
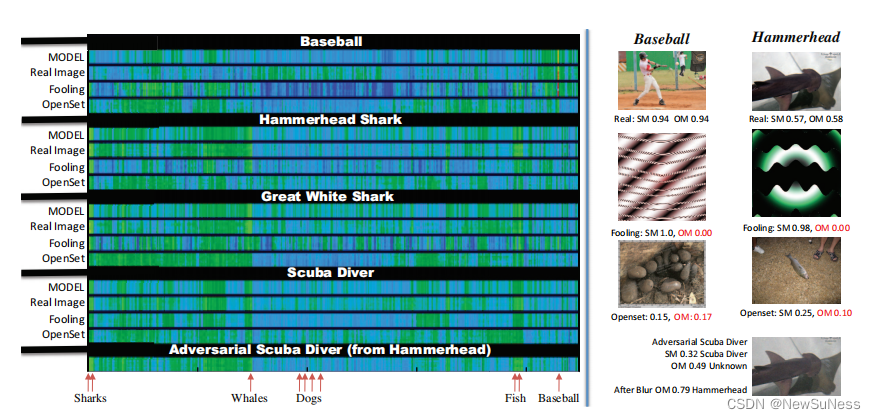
上图展示了激活向量模型如何为元识别和深度网络的OpenMax扩展提供足够的信息,以支持开放集识别。OpenMax算法测量输入的激活向量(AV)和前几个类的模型向量之间的距离,调整分数并提供未知概率的估计。图片中的左边部分展示了不同图片的激活向量,不同的向量之间用黑线隔开。每个输入对应一个激活向量,竖直方向上表示(这块还没搞懂),水平方向表示对ImageNet上前450个类别的响应。
左边的部分展示了真实图片与欺骗图片和开放集图片之间的区别,当OM为红色即表示网络人为该类是未知类。
5、开放集深度网络
将一个深度模型变为可识别开放集,首先想到的就是对输出的概率应用一个阈值来进行过滤,这种方法可以拒绝不确定的预测(比如预测出来所有类别分数都不高),进而再一定程度上使模型可以拒绝未知类别。但是该方法只适合在小部分数据集上使用而不具有泛化能力。Scheirer等人将开放空间风险定义为与标记数据与已知训练样本“很远”相关的风险。这项工作只提供了一个一般的定义,并没有规定如何测量距离,也没有规定要测量这种距离的空间。为了使深度网络能够处理开放集识别,我们必须确保它们能够管理/最小化其开放空间风险,并具有拒绝未知输入的能力。
在此基础上,作者尝试寻找某一层的输出(又称为特征空间)来建立一个紧凑的减弱概率模型,可以通过阈值来限制开放空间风险。模型通过估计已知训练数据距离的空间和元识别方法,然后将这种距离纳入深度网络决策函数。作者称该方法为OpenMax,作为SoftMax功能的替代品。作者证明了整个模型是一个紧致的减弱概率模型,因此,它满足一个开集识别的定义。
6、多类元识别(Multi-class Meta-Recognition)
首先,需要确定模型的输入是否是来自一个未知类别,作者在此使用了元识别的方法来分析系统所给出的分数是否正确。先前的工作中使用了最终的系统分数,基于极值理论(EVT)分析了它们的分布,发现这些分布遵循威布尔分布。虽然人们可以独立使用每个类的分数并使用EVT考虑它们的分布,但这不会产生一个紧凑的减弱概率,因为欺骗图像显示分数本身不是来自一个近距离的已知输入训练数据的紧凑空间。此外,SoftMax层输出的直接EVT拟合对于深度网络没有意义,因为最终的SoftMax层被有意地正则化以遵循逻辑分布。因此,我们分析倒数第二层,它通常被视为每类的估计。这个每类的估计被SoftMax函数转换为最终的输出概率。
(1)EVT理论与元识别算法

(2)OpenMax层工作原理
在EVT拟合完成后,OpenMax层工作流程如下:
