声明:文章参考数学建模清风的网课编写。
最小二乘法
多元线性回归,假设 x 1 , x 2 , . . . , x p x_{1},x_{2},...,x_{p} x1?,x2?,...,xp?是自变量, y y y是因变量,且满足如下线性关系: y i = β 0 + ∑ j β j ? x i j + μ i , ?? i = 1 , 2 , . . . , n ; ?? j = 1 , 2 , . . . , p ; y_{i} = \beta _{0} + \sum_{j}\beta _{j} \ x_{ij} + \mu _{i}, \ \ i = 1, 2, ..., n; \ \ j = 1, 2, ..., p; yi?=β0?+j∑?βj??xij?+μi?,??i=1,2,...,n;??j=1,2,...,p;其中 β 0 , β 1 , . . . , β p \beta _{0},\beta _{1},...,\beta _{p} β0?,β1?,...,βp?为回归系数, μ i \mu_{i} μi?为无法观测且满足一定条件的扰动项。
一般求解多元线性回归系数使用的方法为:普通最小二乘法(OLS)。
那么,最小二乘法是如何求解回归系数呢?
β
^
\hat{\beta}
β^?的取值依赖于,预测值与真实值的偏差
∑
i
=
1
n
∣
y
i
?
y
i
^
∣
\sum_{i=1}^{n} |y_{i} - \hat{y_{i}}|
∑i=1n?∣yi??yi?^?∣。预测值与真实值的偏差最小时取得
β
^
\hat{\beta}
β^?。
μ
i
\mu_{i}
μi?被称为残差
∣
y
i
?
y
i
^
∣
|y_{i} - \hat{y_{i}}|
∣yi??yi?^?∣。
可以理解为:线性回归就是从对原始数据拟合的多条直线中取了偏差最小的一条。
最小二乘法求解回归系数步骤:
1.建立方程,即误差与系数之间的方程。当误差值取最小时的系数即为回归系数:
设有n个因变量
Y
Y
Y以及n列自变量
X
X
X:
Y
=
[
y
1
y
2
?
y
n
]
,
X
=
[
X
1
,
X
2
,
.
.
.
,
X
n
]
=
[
x
11
x
12
…
x
1
n
x
21
x
22
…
x
2
n
?
?
?
?
x
p
1
x
p
2
…
x
p
n
]
Y = \begin{bmatrix} y_{1}\\ y_{2}\\ \vdots \\ y_{n} \end{bmatrix}, X = \begin{bmatrix} X_{1}, X_{2} , ... , X_{n} \end{bmatrix} = \begin{bmatrix} x_{11}& x_{12}& \dots & x_{1n}\\ x_{21}& x_{22}& \dots & x_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ x_{p1}& x_{p2}& \dots & x_{pn} \end{bmatrix}
Y=?
??y1?y2??yn???
??,X=[X1?,X2?,...,Xn??]=?
??x11?x21??xp1??x12?x22??xp2??……?…?x1n?x2n??xpn???
??我们可以找到一组系数:
β
=
[
β
1
β
2
?
β
p
]
\beta = \begin{bmatrix} \beta_{1}\\ \beta_{2}\\ \vdots \\ \beta_{p} \end{bmatrix}
β=?
??β1?β2??βp???
??使得
X
′
β
X'\beta
X′β(矩阵运算)的值尽可能接近
Y
Y
Y:
Y
^
=
X
′
β
=
[
X
1
′
β
X
2
′
β
?
X
n
′
β
]
\hat{Y} = X' \beta = \begin{bmatrix} X_{1}'\beta \\ X_{2}'\beta\\ \vdots \\ X_{n}'\beta \end{bmatrix}
Y^=X′β=?
??X1′?βX2′?β?Xn′?β??
??定义误差(接近程度)为:
Y
?
Y
^
=
Y
?
X
′
β
=
[
Y
1
?
X
1
′
β
Y
2
?
X
2
′
β
?
Y
n
?
X
n
′
β
]
Y - \hat{Y} = Y - X' \beta = \begin{bmatrix} Y_{1} - X_{1}'\beta \\ Y_{2} - X_{2}'\beta\\ \vdots \\ Y_{n} - X_{n}'\beta \end{bmatrix}
Y?Y^=Y?X′β=?
??Y1??X1′?βY2??X2′?β?Yn??Xn′?β??
??进一步消除误差的符号,对每一项平方再相加。得到接近程度的最终表示式:
L
=
(
Y
?
Y
^
)
′
(
Y
?
Y
^
)
=
[
Y
1
?
X
1
′
β
,
???
Y
2
?
X
2
′
β
,
.
.
.
,
???
Y
n
?
X
n
′
β
]
[
Y
1
?
X
1
′
β
Y
2
?
X
2
′
β
?
Y
n
?
X
n
′
β
]
\begin{align*} L &= (Y - \hat{Y})'(Y - \hat{Y}) \\ &= \left [ Y_{1} - X_{1}'\beta, \ \ \ Y_{2} - X_{2}'\beta,..., \ \ \ Y_{n} - X_{n}'\beta\right ]\begin{bmatrix} Y_{1} - X_{1}'\beta \\ Y_{2} - X_{2}'\beta\\ \vdots \\ Y_{n} - X_{n}'\beta \end{bmatrix} \end{align*}
L?=(Y?Y^)′(Y?Y^)=[Y1??X1′?β,???Y2??X2′?β,...,???Yn??Xn′?β]?
??Y1??X1′?βY2??X2′?β?Yn??Xn′?β??
???
2.对建立的方程求导。利用一阶导数为0,二阶导数大于零求最小值:
对
L
L
L求导涉及对矩阵求导,因此这里只给出求导结果(这里使用
β
^
\hat{\beta}
β^?,因为求解出的是系数的估计值):
?
L
?
β
^
=
?
2
X
′
Y
+
2
X
′
X
β
^
\frac{\partial L}{\partial \hat{\beta} } = -2X'Y + 2X'X\hat{\beta}
?β^??L?=?2X′Y+2X′Xβ^?
可以求出并证明二阶导数是大于0的,由一阶导数可以得到: β ^ = ( X ′ X ) ? 1 Y \hat{\beta} = (X'X)^{-1}Y β^?=(X′X)?1Y时误差最小,此时取得回归系数的估计值。
最小二乘法存在的问题:
由回归系数表达式
β
^
=
(
X
′
X
)
?
1
Y
\hat{\beta} = (X'X)^{-1}Y
β^?=(X′X)?1Y,其中
(
X
′
X
)
?
1
(X'X)^{-1}
(X′X)?1读作:X的转置乘X的逆。
可知使用最小二乘法估计回归系数必须要求X的转置乘X的逆存在,而当自变量存在完全多重共线性时会导致X的转置乘X的逆不存在。
那么,如何解决这一问题呢?
岭回归
岭回归通过调整误差方程: L = ( Y ? Y ^ ) ′ ( Y ? Y ^ ) + λ ∑ i = 1 p β i 2 , ???? λ > 1 L = (Y - \hat{Y})'(Y - \hat{Y}) + \lambda \sum_{i=1}^{p} \beta _{i}^{2}, \ \ \ \ \lambda> 1 L=(Y?Y^)′(Y?Y^)+λi=1∑p?βi2?,????λ>1经过调整后,对方程求导: ? L ? β ^ = ? 2 X ′ Y + 2 X ′ X β ^ + 2 λ β ^ \frac{\partial L}{\partial \hat{\beta} } = -2X'Y + 2X'X\hat{\beta}+2\lambda\hat{\beta} ?β^??L?=?2X′Y+2X′Xβ^?+2λβ^?可以求出并证明二阶导数是大于0的,由一阶导数可以得到: β ^ = ( X ′ X + λ I ) ? 1 X ′ Y \hat{\beta} = (X'X+\lambda I)^{-1}X'Y β^?=(X′X+λI)?1X′Y可以证明:当 λ > 1 \lambda> 1 λ>1时, ( X ′ X + λ I ) ? 1 (X'X+\lambda I)^{-1} (X′X+λI)?1总是存在的问题迎刃而解。
岭回归需要选择合适的 λ \lambda λ值:
使用最小化均方误差的方式估计 λ \lambda λ值:我们使? K 折交叉验证的?法来选择最佳的调整参数。所谓的K 折交叉验证,是说将样本数据随机分为 K 个等分。将第 1 个?样本作为 “验证集”(validation set)?保留不?,?使?其余 K-1 个?样本作为 “训练集”(training set)来估计此模型,再以此预测第 1 个?样本,并计算第1个?样本的 “均?预测误差”(Mean Squared Prediction Error)。其次,将第 2 个?样本作为验证集,?使?其余 K-1 个?样本作为训练集来预测第2个?样本,并计算第 2 个?样本的 MSPE。以此类推,将所有?样本的 MSPE 加总,即可得整个样本的 MSPE。最后,选择调整参数 ,使得整个样本的 MSPE 最?,故具有最佳的预测能?。
Lasso回归
与岭回归基本相同,此时: L = ( Y ? Y ^ ) ′ ( Y ? Y ^ ) + λ ∑ i = 1 p ∣ β i ∣ L = (Y - \hat{Y})'(Y - \hat{Y}) + \lambda \sum_{i=1}^{p} |\beta _{i}| L=(Y?Y^)′(Y?Y^)+λi=1∑p?∣βi?∣Lasso回归与相比,最大特点是可以将不重要的变量回归系数压缩至0(可以用来筛选变量,相当于高级逐步回归),岭回归虽然也对原本的系数进行了一定程度上的压缩,但不会压缩为0,最终会保留所有变量。
缺点是:无显式解,只能使用近似估计算法,估计结果不稳定存在误差。
Stata进行Lasso回归
-
安装lassopack(已安装可忽略这一步):
输入findit lassopack并回车;点击蓝色链接:

点击安装:

等待安装完毕即可。 -
对变量进行标准化,即统一量纲。
岭回归和Lasso回归的调整项是直接相加的,因此如果量纲不统一,则计算结果是无意义的。可以使用matlabzscore()命令,或excel对数据进行预处理。 -
Lasso回归命令:
cvlasso y x1 x2 ... xn, lopt seed(520)lopt表示选择使MSPE最小的 λ \lambda λ;
选项seed(520)表示将随机数种子设为520(可以变动),以便结果具有可重复性;
默认K=10即10折交叉验证。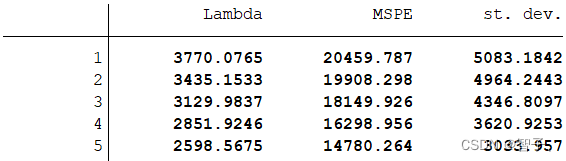
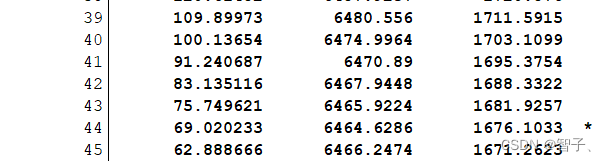
打星号处的 λ=69.02,这是使 MSPE 最小的调整参数。
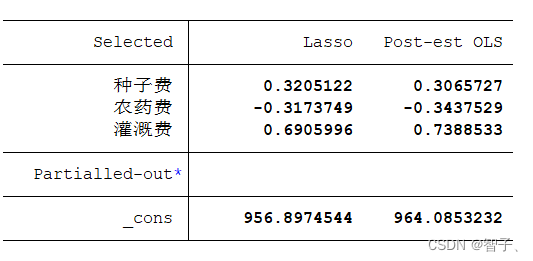
上表右边第 1 列即为 Lasso 所估计的变量系数。其中,除常数项外,只有 3 个变量的系数为非零,而其余变量(未出现在表中)的系数则为 0。考虑到作为收缩估计量的 Lasso 存在偏差(bias),上表右边第 2 列汇报了 “Post Lasso” 估计量的结果,即仅使用 Lasso 进行变量筛选,然后扔掉 Lasso 的回归系数,再对筛选出来的变量进行 OLS 回归。注意:以上结果可能随着我们之前设置的随机数种子变化,因为lasso回归的估计是近似算法,且剔除的多重共线性变量是相对的。
什么情况使用Lasso回归
当变量存在多重共线性时,方差膨胀因子VIF>10则说明存在多重共线性的问题,此时我们需要对变量进行筛选。
使用Lasso回归得到了重要变量后,我们实际上就完成了变量筛选,此时我们只将这些重要变量视为自变量,然后进行回归,并分析回归结果即可。(注意:此时的变量可以是标准化前的,也可以是标准化后的,因为lasso只起到变量筛选的目的)。