[人工智能]13-无监督学习概论

1. 无监督学习基本原理

无监督学习：从无标注数据中学习数据的统计规律或内在结构的机器学习。

• 输入：无标注数据
• 模型：函数 $z=g_{\theta }(x)$，条件概率分布$P_{\theta }(z|x)$,或者条件概率分布$P_{\theta }(x|z)$
• 输出：表示对样本的分析结果，如类别，转换，概率
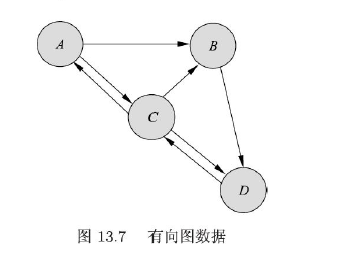
• 基本思想：对给定数据（矩阵数据）进行某种“压缩”，找到数据的潜在结构，假定损失最小的压缩得到的结果就是最本质的结构。其中主要分为聚类，降维，概率模型。
• 聚类：发掘数据纵向结构，把相似样本进行归类。
• 降维：发掘数据横向结构，把高维空间向量转换为低维空间
• 概率模型：发掘数据纵向和横向结构，从数据中学习概率模型。
  

2 基本问题

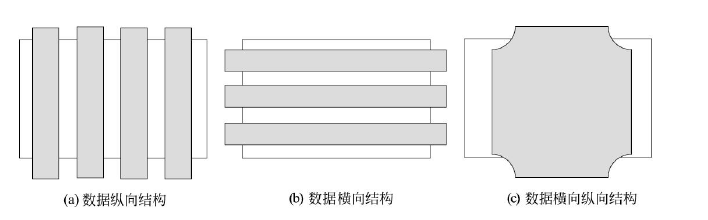
2.1 聚类

聚类(clustering)：是将样本集合中相似的样本分配到相同的类，不相似的样本分配到不同的类。

• 输入：欧式空间的向量，以及给定类别个数
• 模型：
  • 聚类(hard clustering)-一个样本只属于一类，模型是函数$z=g_{\theta }(x)$，确定为某一类
  • 软聚类{soft clustering}-一个样本可以属于多类，模型是$P_{\theta }(z|x)$，确定为某一类的概率
• 其他：层次聚类，K均值聚类
  

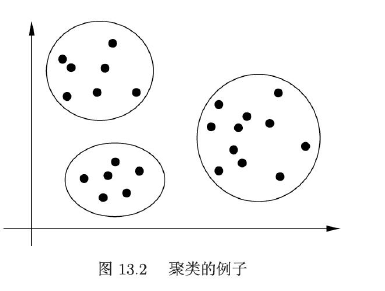
2.2 降维

降维-dimensionality reduction :将样本从高维空间转换到低维空间。

• 降维可以帮助发现数据中隐藏的横向结构
• 通过降维可以更好地表示样本数据的结构，更好地表示样本之间的关系
• 降维有线性降维和非线性降维，降维方法有主成分分析
  -

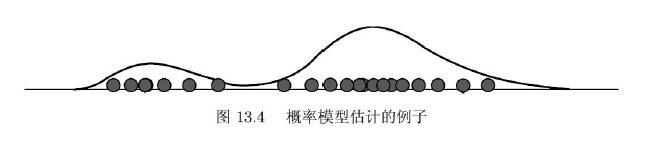
2.3 概率模型估计

概率模型估计-probability model estimation：假设训练数据由一个概率模型生成，由训练数据学习概率模型的结构和参数。

• 学习目标：找到最有可能生成数据的结构和参数
• 概率模型估计可以帮助发现数据中隐藏的横向纵向结构
• 概率模型包括混合模型、概率图模型等
  • 概率图模型又包括有向图模型和无向图模型
    

3 机器学习三要素

无监督学习三要素：模型、策略、算法

模型：就是函数 $z=g_{\theta }(x)$，条件概率分布 $P_{\theta }(z|x)$，或$P_{\theta }(x|z)$，在聚类、降维、概率模型估计中拥有不同的形式

• 聚类模型的输出是类别
• 降维 中模型的输出是 低维向量
• 概率模型估计 中的模型可以是混合概率模型，也可以是有向概率图模型和无向概率图模型

策略：在不同的问题中有不同的形式，但都可以表示为目标函数的优化

• 聚类中样本与所属类别中心距离的最小化
• 降维中样本从高维空间转换到低维空间过程中信息损失的最小化
• 概率模型估计中模型生成数据概率的最大化

算法: 通常是迭代算法，通过迭代达到目标函数的最优化，比如，梯度下降法。

• 层次聚类法，K均值聚类是硬聚类方法
• 高斯混合模型，EM算法是软聚类方法
• 主成分分析，潜在语义分析是降维方法
• 概率潜在语义分析、潜在狄利克雷分配 是概率模型估计方法

4 无监督学习方法

4.1 聚类

聚类：主要用于数据分析，也可以用于监督学习的前处理

• 可以帮助发现数据中的统计规律
• 数据通常是连续变量表示的，也可以是离散变量表示的
• 包括层次聚类和K均值聚类

详细内容可参考第14章内容。

4.2 降维

降维：主要用于数据分析，也可以用于监督学习的前处理。

• 降维可以帮助发现高维数据中的统计规律
• 数据是连续变量的

具体方法可参考第16章主成分分析，以及第15章奇异值分解

4.3 话题分析

话题分析：是文本分析的一种技术。给定一个文本集合，话题分析旨在发现文本集合中每个文本的话题，而话题由单词的集合表示。

• 且假设有足够数量的文本
• 话题分析可以形式化为概率模型估计问题，或降维问题

话题分析方法具体可以参考第17，18，20章的潜在语义分析、概率潜在语义分析、潜在狄利克雷分配，以及19章的马尔可夫链蒙特卡罗法。

4.4 图分析

图分析-graph analytics：发掘隐藏在图中的统计规律或潜在结构。

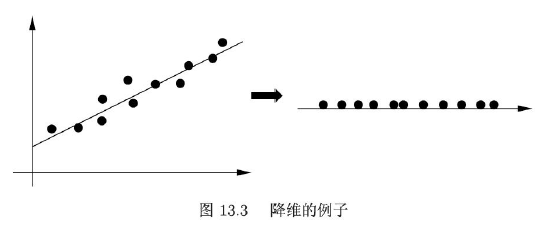
• 数据以图的形式存在，图数据表示实体之间的关系，包括有向图、无向图、超图。
• 链接分析link analysis:发现有向图中的重要节点，包括pagerank算法
• pagerank算法：
  • 一种无监督学习算法
  • 原理：给定有向图，定义马尔可夫链作为随机游走者，不断迭代，根据马尔科夫链的平稳概率得到节点重要性PageRank值。 被指向的结点越多，PageRank值越大，结点越重要。
  • PageRank算法是最初为互联网搜索而提出，将互联网看作是一个巨大的有向图，网页是结点，网页的超链接是有向边。
  • PageRank 算法可以算出网页的PageRank值，表示其重要度，搜索引擎的排序中网页的重要度起着重要作用。