文章目录
Dive into deep learning(05)[动手学深度学习]———————第五章,卷积神经网络
前言:和别的深度学习教学相比,李沐老师的视频真的是。相见恨晚呐
本章摘要:
1、从全连接层到卷积(why-conv)
这里主要是概念的引出。
由于真实图片像素巨大,像之前感知机里面把图片展平做全连接显然不可能,而且图片有空间信息,这也意味着展平会损失这些信息,因此我们的输入应该仍旧是一个矩阵。
矩阵的全连接层是可以实现的。
但是,现在一张图片的像素动不动就千万级别,光是输入层到隐藏层就有千万级别的输入,更别提后面的模型训练了,因此需要先把图片压缩。由此引出了卷积。
在矩阵的全连接层的基础上,基于两个图片拥有的性质。一个是平移不变性,还有一个是局部性,这两个性质让原本的数据得以压缩。使得全连接层的参数大大减少。
(关于具体推导可以看李沐老师的视频,但我自己打算有空的时候额外写一篇记录一下,这里插个眼)
作业:
为什么平移不变性可能也不是好主意呢?
卷积层也适合于文本数据吗?为什么?
(这两个问题记录一下)
函数记录:
2、图像卷积(conv-layer)
卷积的名称其实是引用了傅里叶变换里的卷积,好像还有什么滤波器,深度学习里的卷积公式其实与傅里叶变换中的卷积公式不同。但两者相差不大,且直接用傅里叶变换里的卷积公式也是一样的效果,只不过为了方便,简化了公式,其为互相关计算公式。
之前的神经网络是为了计算权重w和偏置b,而这里的卷积是为了计算卷积核和偏置,卷积核可以看作是权重w的矩阵。卷积核最后可以从提取图片特征这一个点上理解。例如一个关于猫的卷积分类器,一张图片经过卷积可能提取出了有胡须,有鼻子,有眼睛或者更小的类似瞳孔毛发等这些特征信息。在经过多层卷积后,这些细微的特征会不断被放大。最后再通过全连接层,这里的全连接层可以理解为特征的线性组合,可能从图片里提取出来的特征还有狗脚什么的,经过权重分配,最后计算概率。
作业:
函数记录:
3、填充和步幅(padding-and-strides)
这是两个超参数
填充的目的是可以更多的提取边缘信息。
步幅的作用是调节数据维度,并且可以减小数据量。
作业:
对于音频信号,步幅 2 说明什么?
函数记录:
``
4、多输入多输出通道(channels)
在最流行的神经网络架构中,随着神经网络层数的加深,我们常会增加输出通道的维数,通过减少空间分辨率以获得更大的通道深度。直观地说,我们可以将每个通道看作是对不同特征的响应。而现实可能更为复杂一些,因为每个通道不是独立学习的,而是为了共同使用而优化的。因此,多输出通道并不仅是学习多个单通道的检测器。
更直白的说就是不断减小数据矩阵形状大小,不断增多通道,通道可以看出提取出来的图片特征。
作业:
Q1: 假设我们有两个卷积核,大小分别为k_1和k_2(中间没有非线性激活函数)。
- 证明运算可以用单次卷积来表示。
答:参见Google的Inception v3的论文:Rethinking the Inception Architecture for Computer Vision - 这个等效的单个卷积核的维数是多少呢?
答:假设这两个卷积核不是1×1卷积核,且stride=1, padding=0,则可得该等效的单个卷积核的维数k = k_1 + k_2 - 1(如果卷积核k_h和k_w不同,则分别计算)。 - 反之亦然吗?
答:反之亦然,即单个卷积核也可以用两个卷积核等价表示(此时1×1卷积核也成立)。
Q2: 假设输入为c_i×h×w,卷积核大小为c_o×c_i×k_h×k_w,填充为(p_h, p_w),步幅为(s_h, s_w)。
- 前向传播的计算成本(乘法和加法)是多少?
答:c_o×c_i×(?(??𝑘_?+𝑝_?+𝑠_?)/𝑠_??×?(𝑤?𝑘_𝑤+𝑝_𝑤+𝑠_𝑤)/𝑠_𝑤?)×(k_h×k_w + k_h×k_w-1)。 - 内存占用是多少?(是指参数所占的内存?还是指参数以及数据的内存占用?)
答:前者:c_i×h×w+c_o×c_i×k_h×k_w+c_o×?(??𝑘_?+𝑝_?+𝑠_?)/𝑠_??×?(𝑤?𝑘_𝑤+𝑝_𝑤+𝑠_𝑤)/𝑠_𝑤? - 反向传播的内存占用是多少?
答:不会算 - 反向传播的计算成本是多少?
答:不会算
Q3: 如果我们将输入通道c_i和输出通道c_o的数量加倍,计算数量会增加多少?如果我们把填充数量翻一番会怎么样?
A3: 如果输入通道c_i和输出通道c_o的数量加倍,则计算量变为原来的4倍;如果填充数量翻一番,则计算量增加c_o×c_i×(p_w/s_w)×(p_h/s_h)。
Q4: 如果卷积核的高度k_h=k_w=1和宽度是,前向传播的计算复杂度是多少?
A4: c_o×(2×c_i-1)×(h×w)
Q5: 本节最后一个示例中的变量Y1和Y2是否完全相同?为什么?
A5: 因为浮点数计算有误差,所以两者不完全相同,这个我在6.1底下的reply已经通过代码验证过,详情请看https://zh.d2l.ai/chapter_convolutional-neural-networks/why-conv.html
(作业是抄别人的,第一个感觉挺重要的,说明各个卷积层之间得加激活函数,否则就没什么意义)
函数记录:
K = torch.stack((K, K + 1, K + 2), 0)##这里是在K的第0维度上增加一个维度,对K,K+1,K+2这三个矩阵进行拼接(K原本是3阶矩阵,这步操作完之后K变为4阶)
5、汇聚层(pooling)
同时也称为池化层。
降低卷积层对位置的敏感性,同时降低对空间降采样表示的敏感性
汇聚层分为两种
最大汇聚层和平均汇聚层
作业:
Q3: 假设汇聚层的输入大小为c×h×w,则汇聚窗口的形状为p_h×p_w,填充为(p_h,p_w),步幅为(s_h,s_w)。这个汇聚层的计算成本是多少?
A3: 计算成本:c×(?(?+𝑠_?)/𝑠_??×?(𝑤+𝑠_𝑤)/𝑠_𝑤?)×p_h×p_w
Q4: 为什么最大汇聚层和平均汇聚层的工作方式不同?
A4: 没看懂题目啥意思…
Q5: 我们是否需要最小汇聚层?可以用已知函数替换它吗?
A5:
不需要。因为在pooling层之前一般都是activation function,例如relu层,它会将特征值全部转换为大于等于0的值,如果使用min pooling,那么得到的特征图很可能是一大堆的0,当你多次进行min pooling之后,几乎所有的激活值都变为0,造成梯度消失,网络就无法通过bp进行更新了。
可以对数据先×(-1),然后用最大汇聚层,最后再×(-1),得到最小汇聚层。
Q6: 除了平均汇聚层和最大汇聚层,是否有其它函数可以考虑(提示:回想一下softmax)?为什么它不流行?
A6: 将softmax引入汇聚层也可以,但softmax并不改变各个pixel之间的大小关系,在某种程度上与最大汇聚层的效果类似(最终选出的pixel和最大汇聚层选出的pixel一样,只是值不同),但增加了不少的计算量(指数运算),最终效果却不一定比最大汇聚层好。
函数记录:
pool2d = nn.MaxPool2d((2, 3), stride=(2, 3), padding=(0, 1))##最大汇聚层
6、卷积神经网络(LeNet)(lenet)
主要是lenet的构造
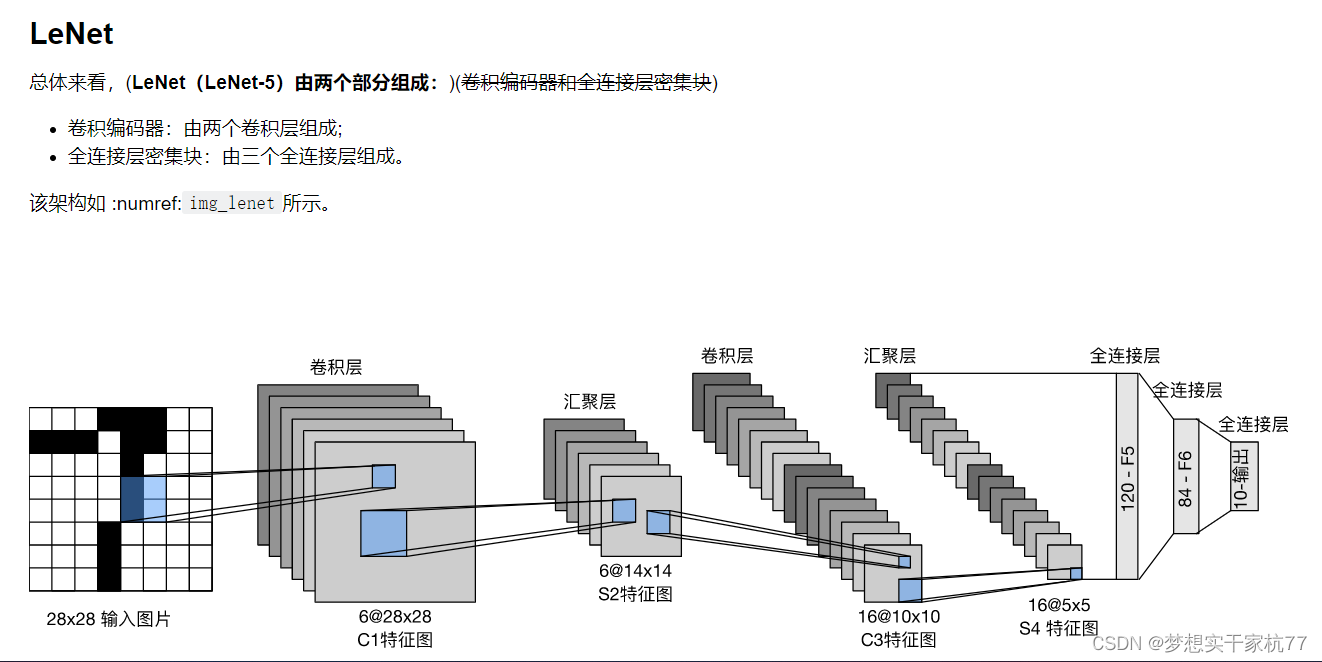
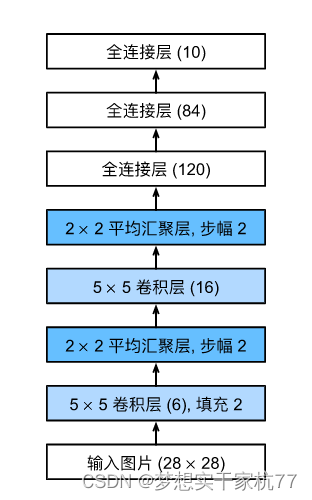
net = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Flatten(),
nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
nn.Linear(120, 84), nn.Sigmoid(),
nn.Linear(84, 10))
作业:
函数记录:
nn.AvgPool2d(kernel_size=2, stride=2)##平均池化层
nn.Conv2d(6, 16, kernel_size=5)##普通的卷积,表示6通道变为16通道