【李宏毅机器学习2021】本系列是针对datawhale《李宏毅机器学习-2022 10月》的学习笔记。本次是对误差和梯度下降的学习总结。本节通过视频学习到对模型调优中面临的系列问题，李宏毅老师列出常见问题树状图，从train的loss开始，到test loss问题，引出训练中的问题并讲解原因，介绍改进方法。
目录
误差和梯度下降
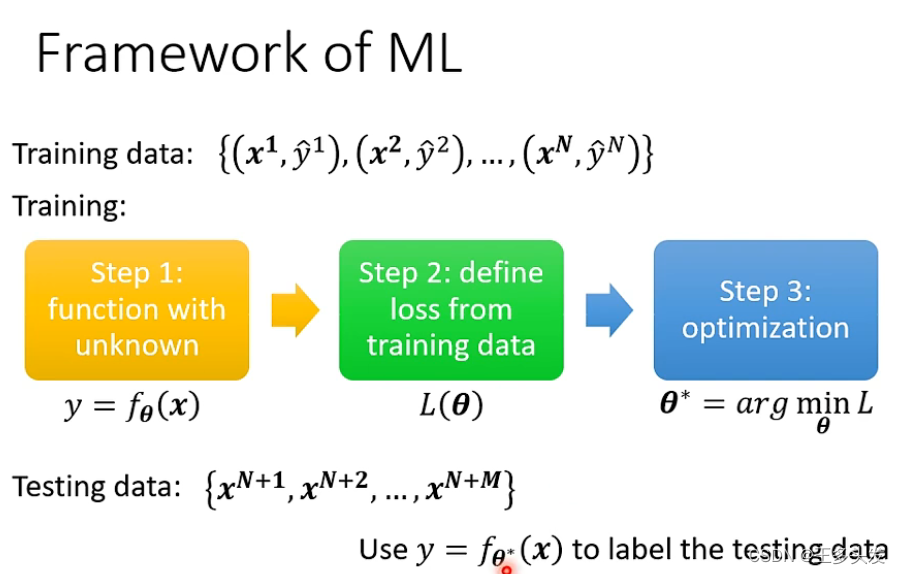
在输入各种数据求得方程的过程中，必不可少的就是让方程计算的y和实际y相差最小，就是loss。从loss入手解决模型问题。?
解决loss问题的大纲如下~
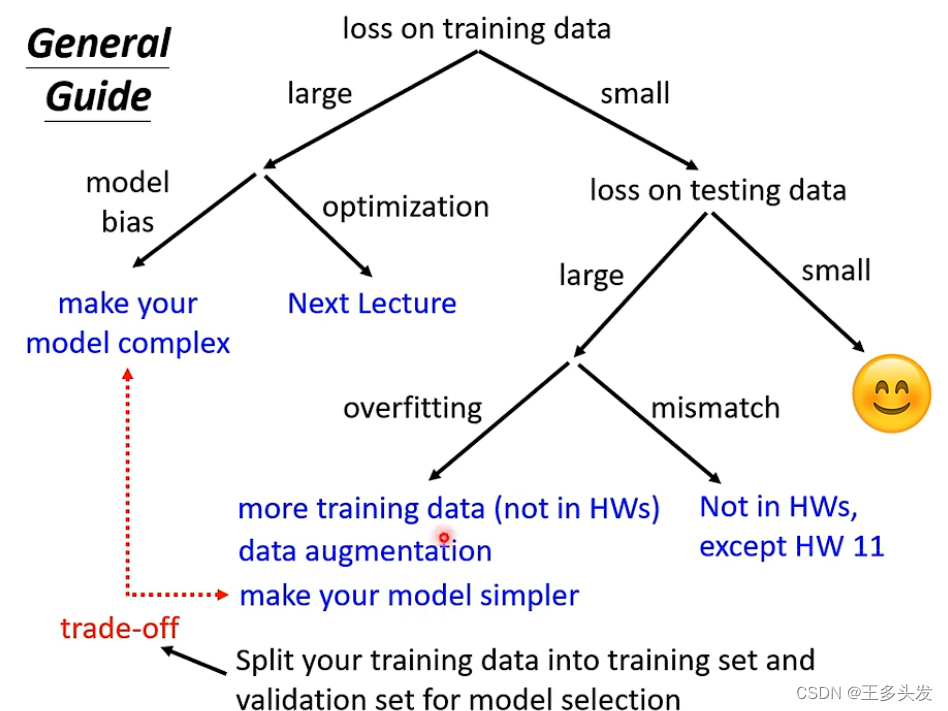
Train data loss
?Model Bias
?模型参数选择的太简单就会导致loss下降过低，可以尝试增加模型复杂度，让模型更具有弹性。有更好的适应性让训练loss下降。
Optimization?
在做梯度下降操作不当也会导致loss不下降的情况。
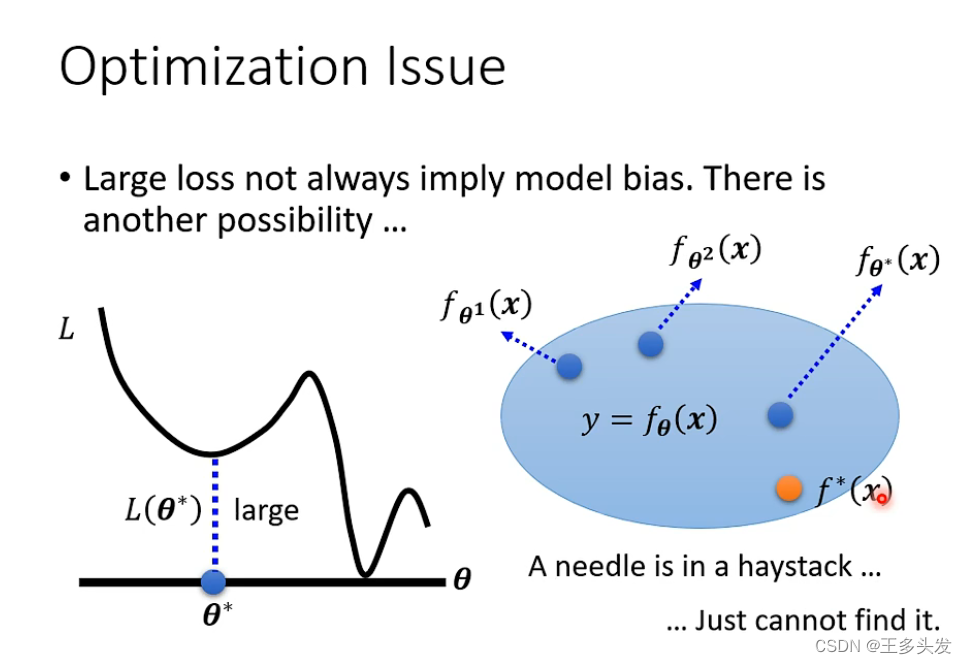
?如何判断优化问题还是Bias问题？
?
?
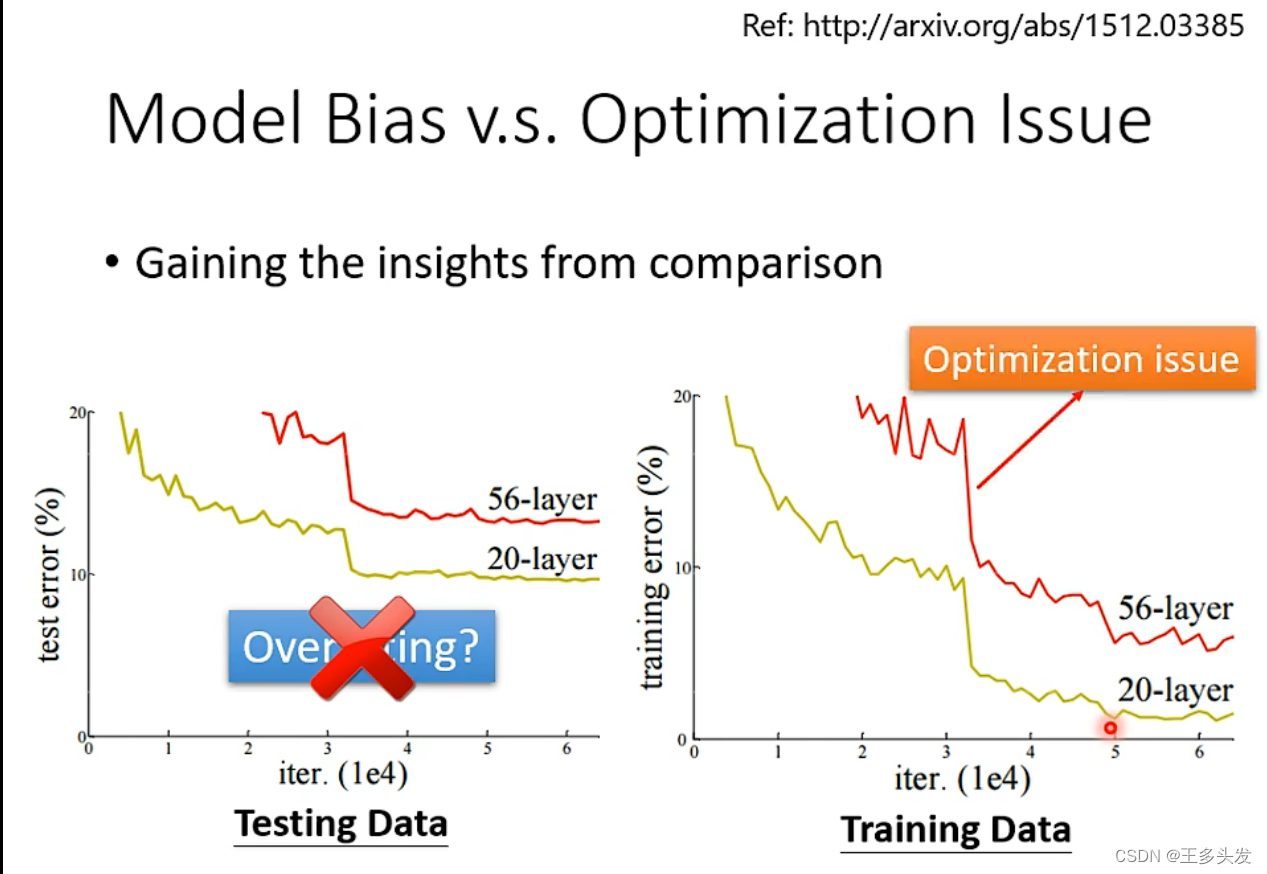
首先强调一下，并不是说你的模型loss降不下去就是过拟合问题。在train阶段可不是这样。
在相同的模型下，减少模型的复杂度，比如100层见到50层看看情况，loss是不是下降的更好。如果更好，可以这样想，100层网络后面50层什么都不做，完全可以达到一样的效果，为什么loss不下降，只能说明是优化器的问题。?因此在无法判断的时候可以采用上述方法定位问题到底在哪里。
后面会介绍opt问题如何解决。
Testing data loss
当然下图是最理想的路线，希望大家的模型都会如期进行啦~
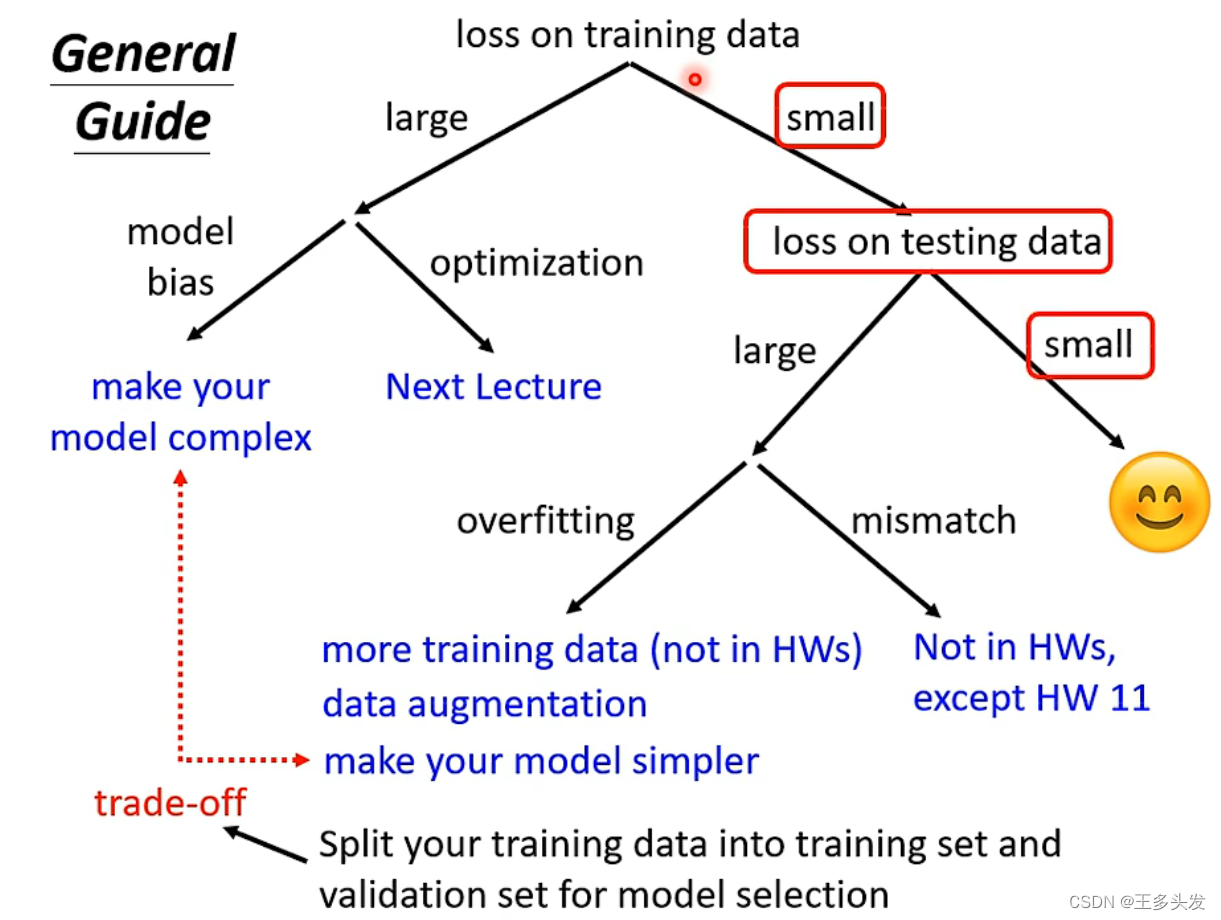
?Overfitting
过拟合在训练过程中往往是一个让人头痛的问题……不过也有办法处理。如何判断over fitting呢？就是你训练集loss很低，但是trainingloss高的离谱，这就是overfitting问题。
?产生的原因是拟合的函数与实际函数相差过大，但在训练时以为训练数据的原因导致数据匹配到曲线上误认为模型鲁棒性很好。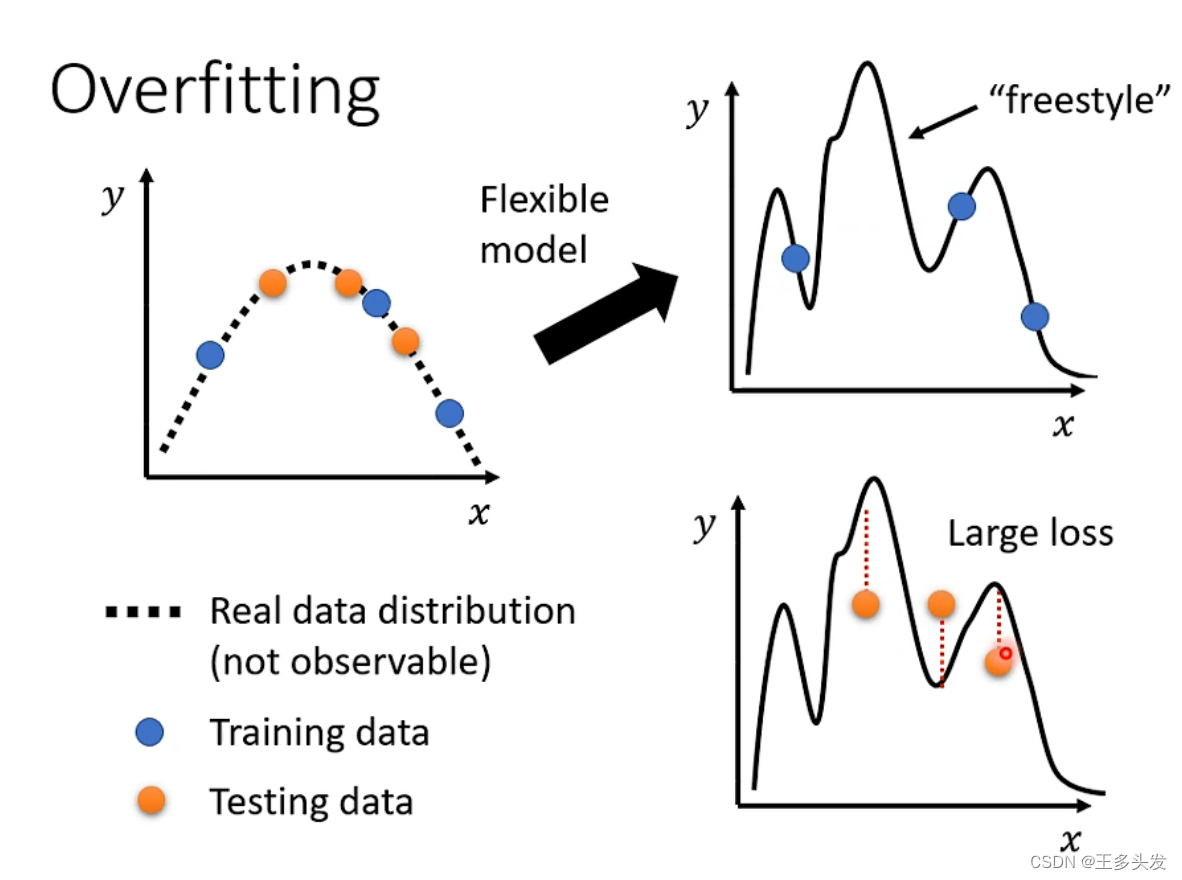
?可以加入更多数据，保证模型的准确性?。在学习阶段不建议扩充数据集，建议对数据按照逻辑进行变换扩充。例如楼下猫猫。
?为了减少模型弹性解决办法综述如上：
这里还一个问题，就是模型的复杂性和loss这里有些矛盾。模型不能太简单，训练效果不好，模型不能太复杂，会过拟合。
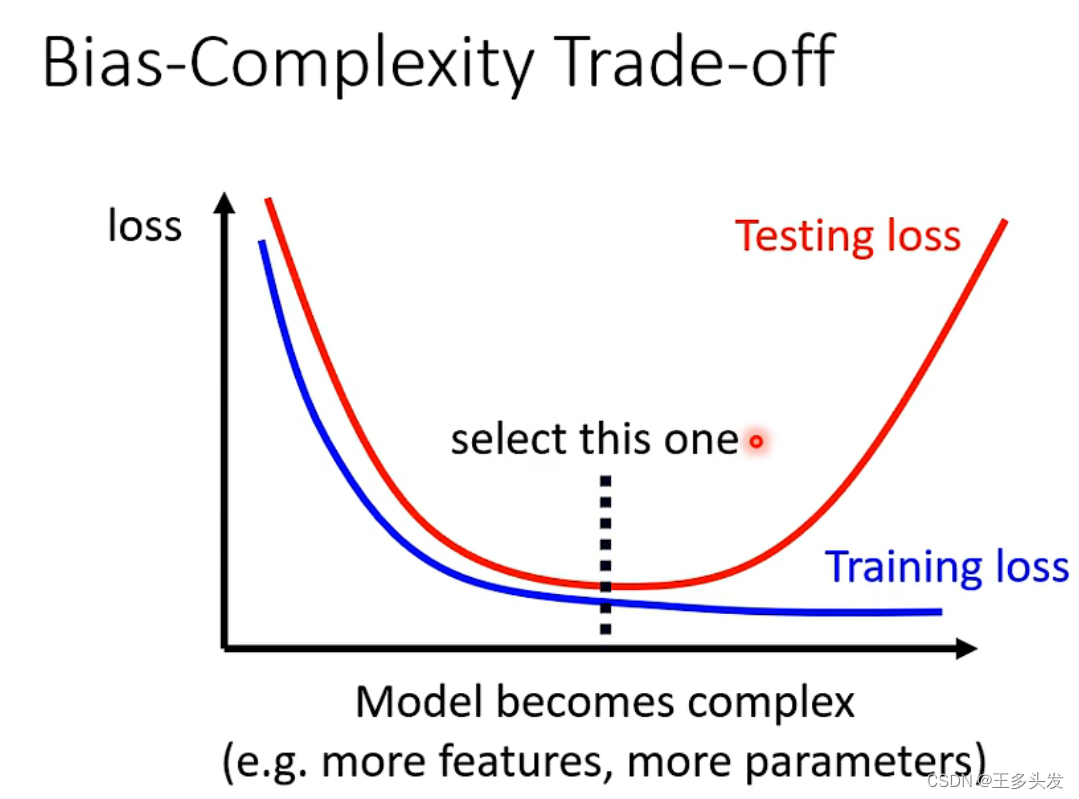
?这里为了解决这个办法大家肯定会选一个在测试集loss低一些的模型，但是有可能是因为测试集效果因为模型恰好匹配这里的数据。一般比赛会将数据分为公共和私用两个测试集。可能你在公共得了高分并不一定在私用也是高分……这个也可以推广到其它问题，比如你在A数据集分数很高，但是迁移后就不行了，可能并不具有很好的普适性……
?这里提出交叉验证方法：将数据分为K部分，每次用一部分测试其他部分训练，轮流反转得到k个模型，再验证后得到在k个数据上效果最好的模型为最终模型。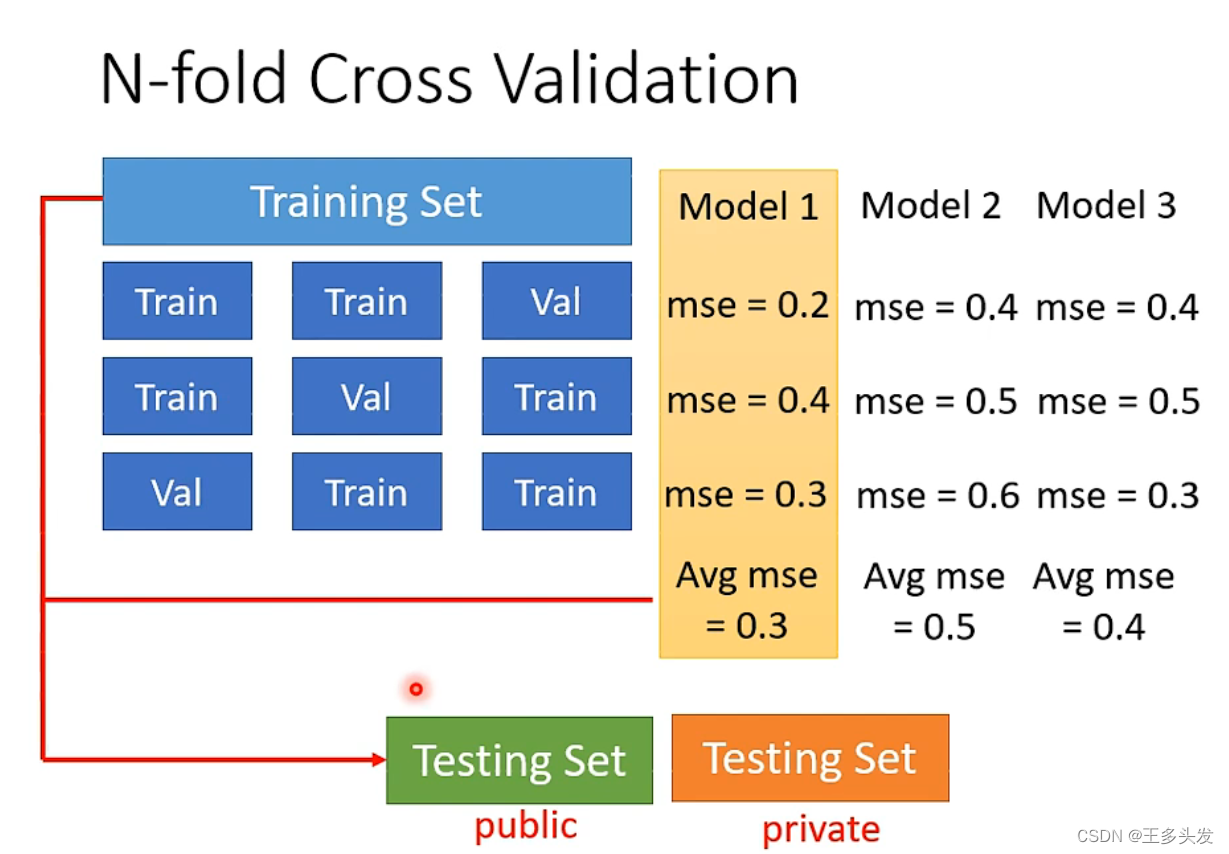
?MisMatch
?上节课留下问题就是说26号的观看人数问题，结果计算机认为周五看得人应该少，但是因为上课的原因导致看得人很多。因为训练和测试数据差异过大会导致这个问题。
?
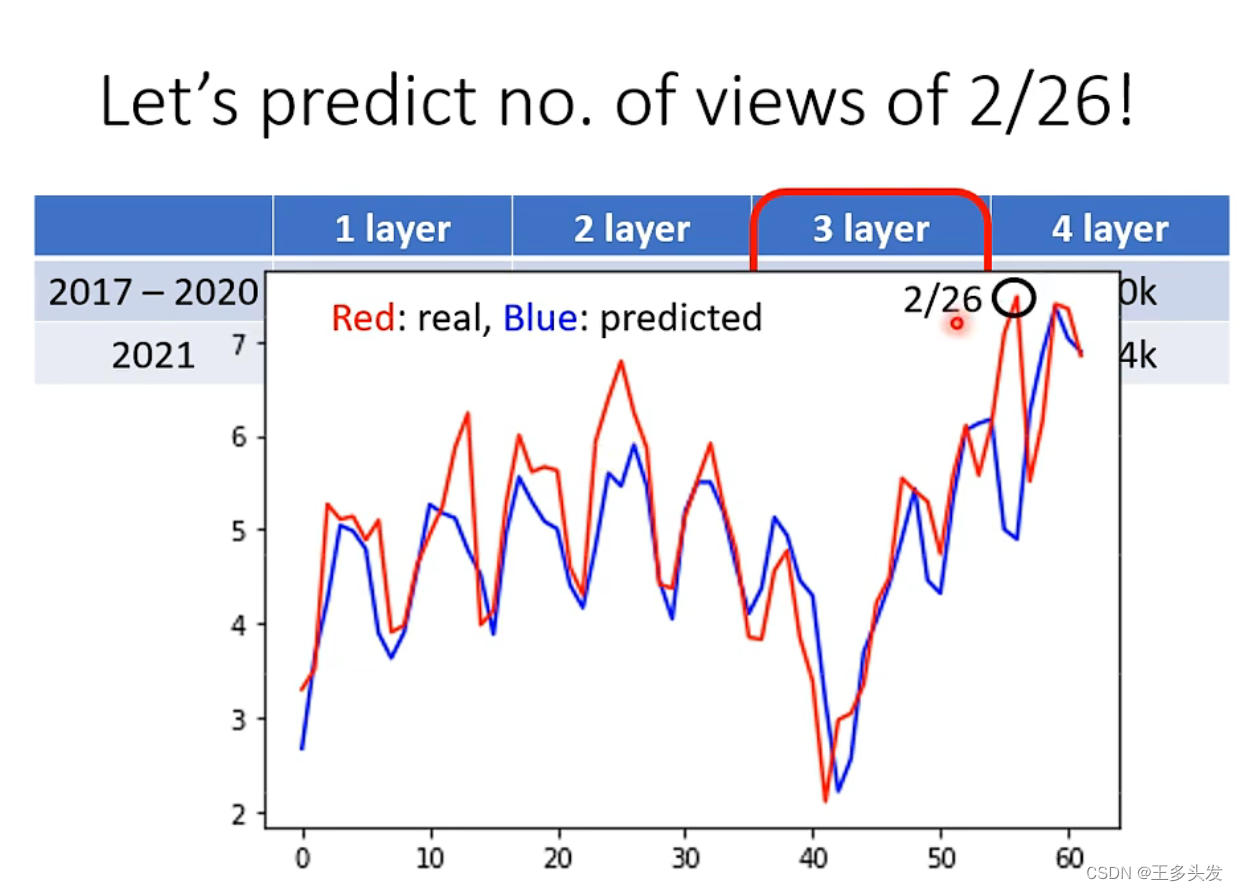
?Optimization失败如何处理
失败原因
往往在训练过程中不只有在数据到local minima or local maxima点会导致梯度为零，在saddle point也会导致梯度为零。在这里就会让loss不再下降，给训练带来大模型loss反而降不下去的问题。
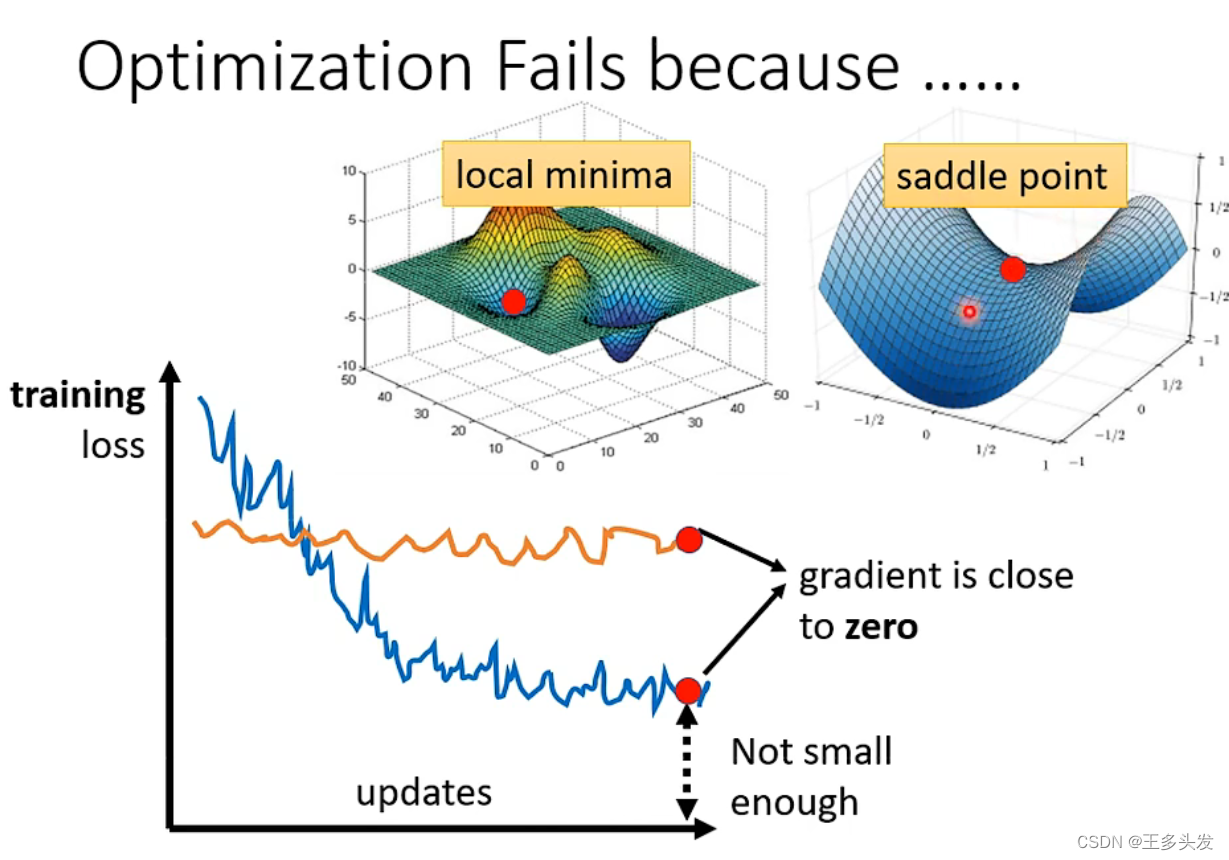
?如何判断saddle point？
答案就是通过下式中两个临近loss曲线上的点公式，在鞍点或者局部最小/大点会导致g为零。通过判断H的正负性去判断L(θ)和L(θ')大小。从而判断鞍点还是局部最小/大点。
?
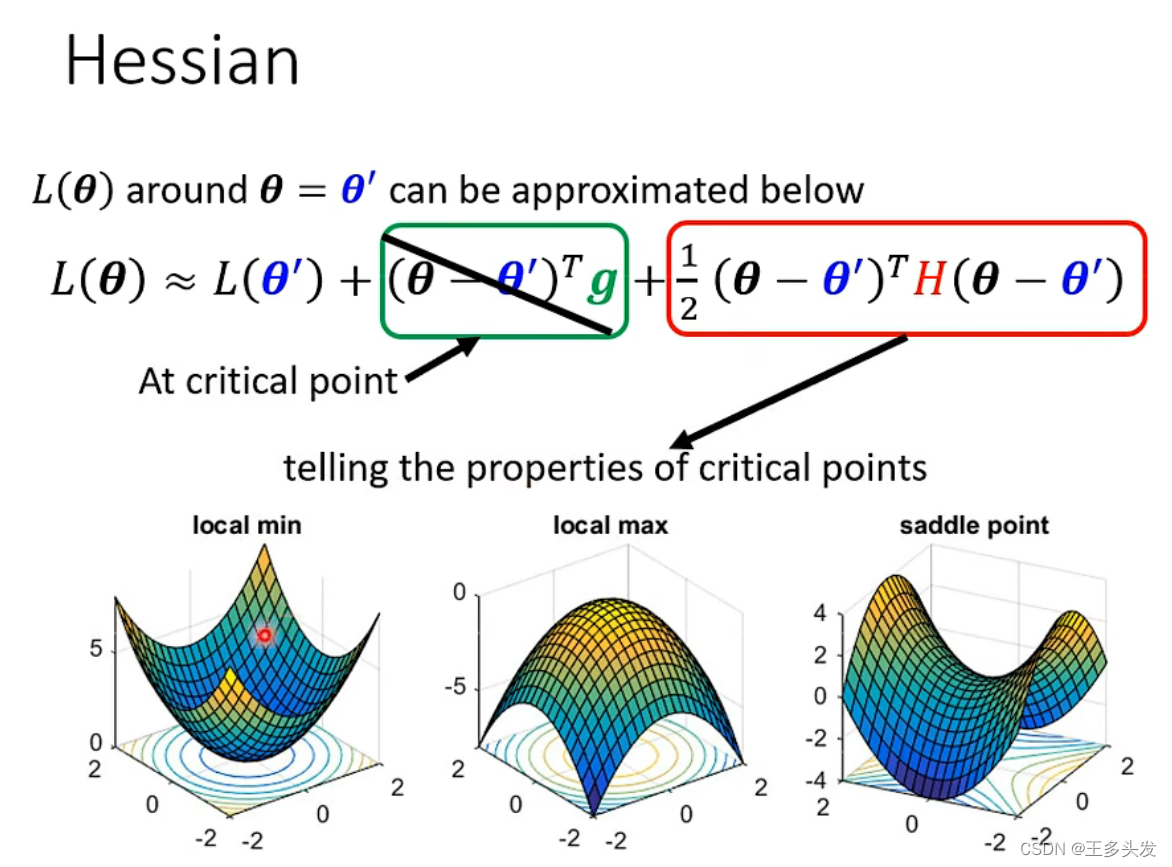
这里的H指的是海塞矩阵，即计算式中海塞矩阵的值的情况判断。
如果H大于0? 表示?θ'局部最小点
如果H小于0? 表示?θ'局部最大点
如果H解符号不唯一 说明是鞍点
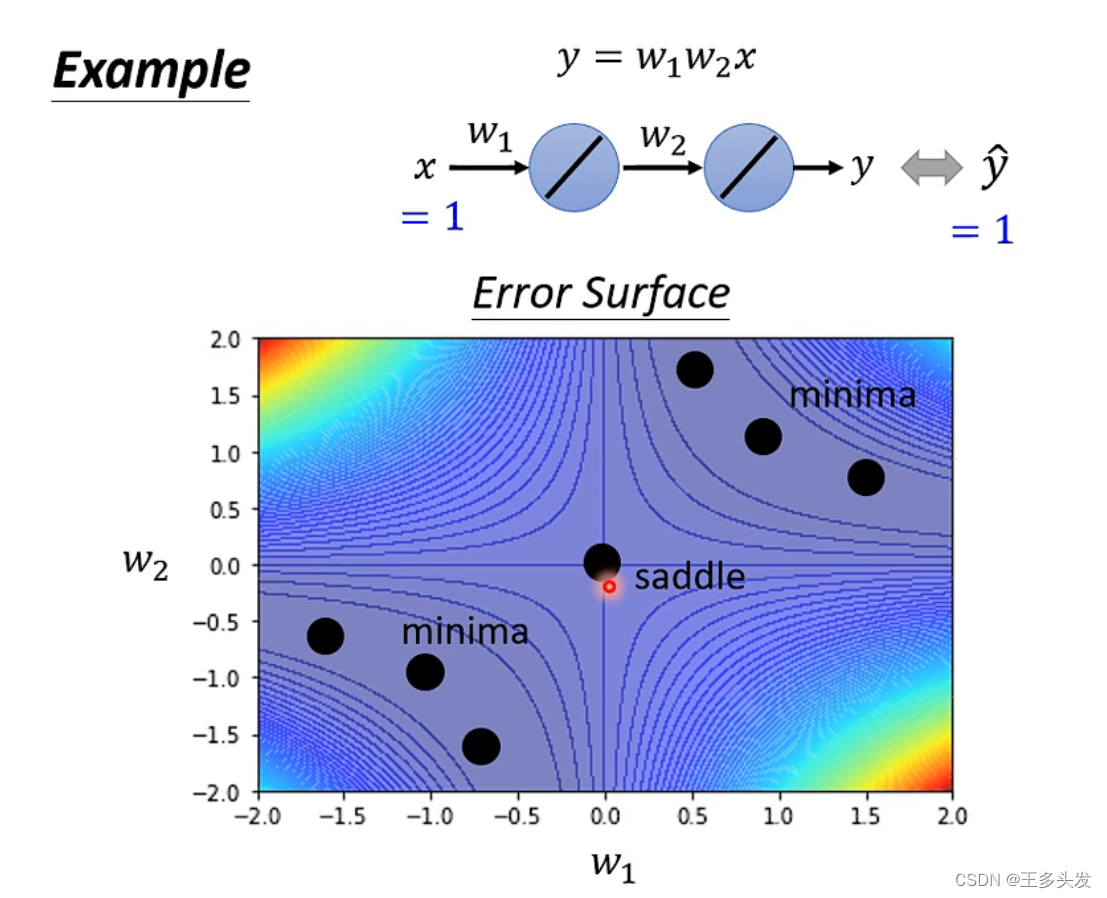
实例计算鞍点?
?
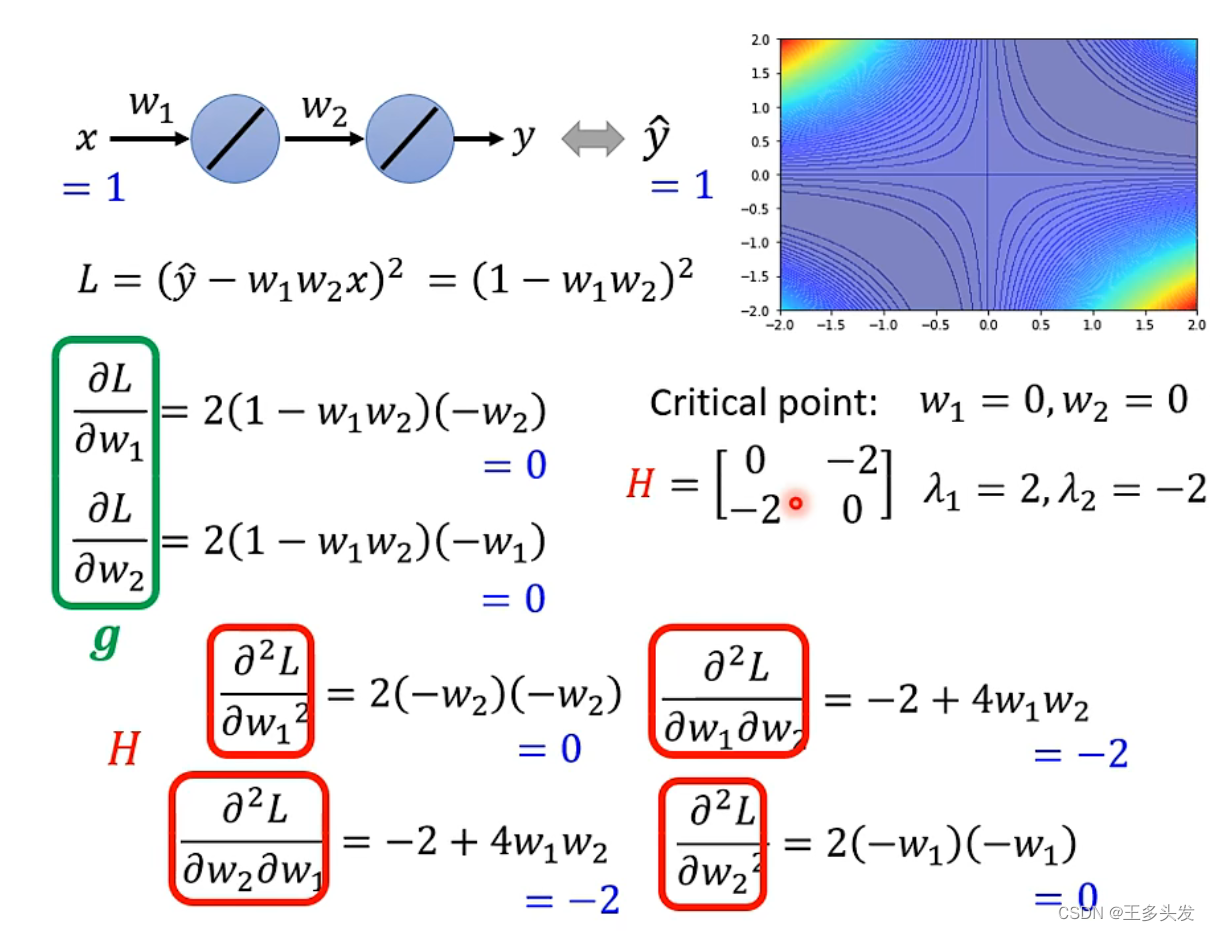
?这里其实计算海塞矩阵的特征值，即可判断是否为鞍点。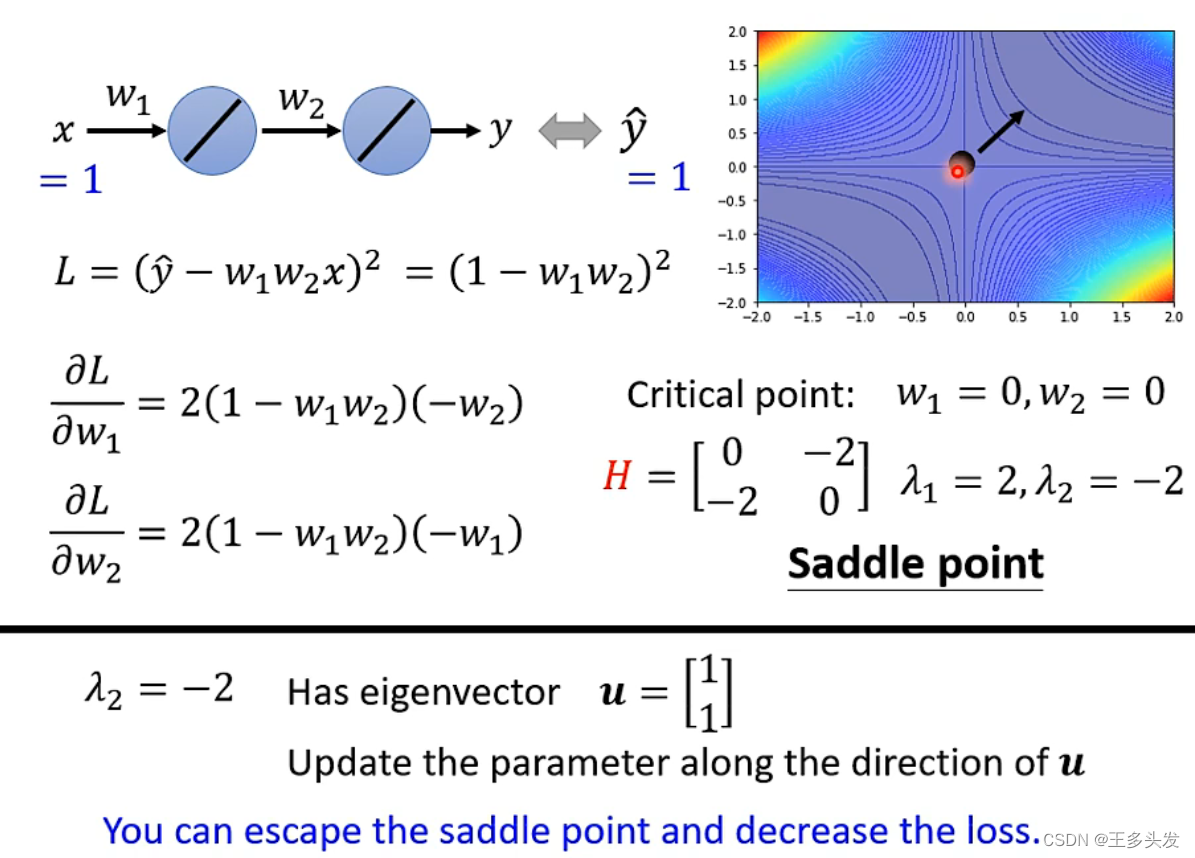
而海塞矩阵的特征向量即为梯度下降的方向，可以跳出鞍点这个坑了！！！
后面会讲opt相关的方法吧，先挖个坑深度学习：鞍点以及如何跳出鞍点_Way_X的博客-CSDN博客_鞍点函数
?鞍点和局部最小值谁更常见呢？
如果处处都是局部最小值，即使求得了也不愿意用。可能算出来的点并不是很理想。就好比你扔弹珠，想扔到一个比较深的坑里，但是在必经之路上有很对小坑，想弹进去很麻烦，总是被小坑拦住去路。不过在深度学习里，一般函数维度都很高，遇到这样的情况并不常见，相对很容易出现鞍点而不是局部最小值。
?
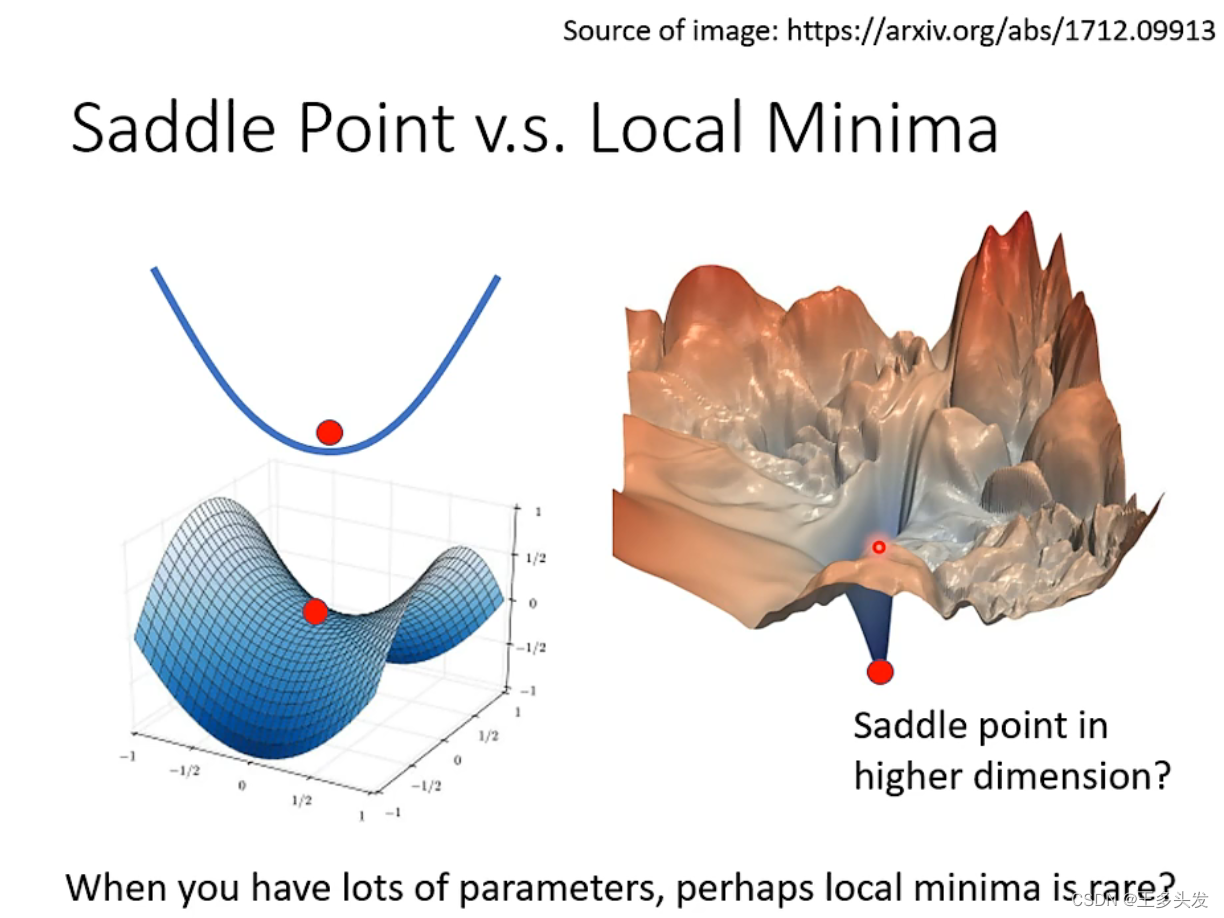
从经验上讲一半以上的维度都没有达到局部最小值……?
【学习总结】通过本次学习加深了对深度学习训练后调优的思路，对opt优化原理也有了更深刻的认识。今天打卡比较晚啦，下次早点不浪了~~
?