第一部分·单项选择题
1.下列哪一项在神经网络中引入了非线性(B)
A.随机梯度下降
B.修正线性单元(ReLU)
C.卷积函数
D.以上都不对
卷积函数是线性的,一般情况下,卷积层后会跟一个非线性函数。
Relu函数是非线性激活函数,线性修正单元其实是非线性激活函数
2.关于句子向量表示,下列说法正确的是(C)
A.只能通过有监督学习获得
B.只能通过无监督学习获得
C.有监督和无监督学习都可以获得
D.以上都不对
3.关于梯度下降算法,以下说法正确的是(D)
A.随机梯度下降算法是每次考虑单个样本进行权重更新
B.Mini-Batch梯度下降算法是批量梯度下降和随机梯度下降的折中
C.批量梯度下降算法是每次考虑整个训练集进行权重更新
D.以上都对
1.批量梯度下降算法(Batch Gradient Descent)在整个训练集上计算的,如果数据集比较大,可能会面临内存不足问题,而且其收敛速度一般比较慢。
2.随机梯度下降算法(Stochastic GradientDescent)针对训练集中的一个训练样本计算,又称为在线学习,即得到了一个样本,就可以执行一次参数更新。其收敛速度会快一些,但是有可能出现目标函数值震荡现象。
3.小批量梯度下降算法(Mini-batch Gradient Descent)。选取训练集中一个小批量样本计算,这样可以保证训练过程更稳定,是目前最常用的梯度下降算法。所以是随机和批量梯度下降的折中
4.与传统机器学习方法相比,深度学习的优势在于(A)
A.深度学习可以自动学习特征
B.深度学习完全不需要做数据预处理
C.深度学习完全不提取底层特征,如图像边缘、纹理等
D.深度学习不需要调参
传统的需要人工去提取特征、而深度学习可以自动学习特征
5.如果使用的学习率太大,会导致(C)
A.网络收敛的快
B.网络收敛的慢
C.网络无法收敛
D.不确定
在梯度下降法中,都是给定统一的学习率,整个优化过程中都以确定的步长进行更新,在迭代优化的前期中,学习率较大,则前进的步长就会较长,这时便能以较快的速度进行梯度下降,而在迭代优化后期,逐步减小学习率的值,减小步长,这样有助于算法的收敛,更容易接近最优解。
学习率设置太小,网络收敛非常缓慢。学习率设置太大会造成网络不能收敛,在最优值附近徘徊。
6.在一个神经网络里,知道每一个神经元的权值和偏差值是最重要的一步。如果以某种方法知道了神经元准确的权重和偏差,就可以近似任何函数。实现这个最佳的办法是(C)
A. 随机赋值,祈祷他们是正确的
B. 搜索所有权重和偏差的组合,直到得到最佳值
C. 赋予一个初始值,通过检查跟最佳值的差值,然后迭代更新权重
D. 以上说法都不正确
初始连接权重关系到网络训练速度的快慢以及收敛速率,在基本的神经网络中,这个权重是随机设定的。在网络训练的过程中沿着误差减小的方向不断进行调整。
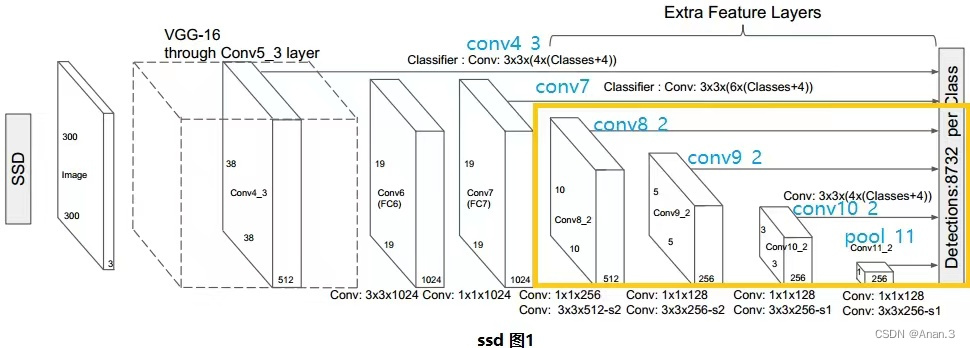
7.SSD主要通过哪种方法来解决检测不同大小目标的问题(C)
A. 设置更多的anchor尺寸
B. 设置更多的anchor纵横化
C. 在不同的特征图上进行预测
D. 使用图像金字塔作为输入
SSD网络进行一次预测的示意图,可以看出,检测过程不仅在填加特征图(conv8_2, conv9_2, conv_10_2, pool_11)上进行,为了保证网络对小目标有很好检测效果,检测过程也在基础网络特征图(conv4_3, conv_7)上进行。
8.当图像分类的准确率不高时,以下哪种方法不能提高准确率(C)
A. 数据增强
B. 调整超参数
C. 减少数据集
D. 使用预训练网络参数
使用数据增强技术(data augmentation),主要是在训练数据上增加微小的扰动或者变化,一方面可以增加训练数据,从而提升模型的泛化能力,另一方面可以增加噪声数据,从而增强模型的鲁棒性
学习率是神经网络训练中最重要的超参数之一,在很多关于神经网络的论文中,都采用了变化学习率的技术来提升模型性能
从模型角度进行一些改进
9.如果增加神经网络的宽度,精确度会增加到一个阈值,然后开始降低。造成这一现象的原因可能是
A. 只有一部分核被用于预测
B. 当核数量增加,其相关性增加,导致过拟合
C. 当核数量增加,神经网络的预测能力降低
D. 以上都不对
如C选项指出的那样,可能的原因是核之间的相关性。
10.下列哪一种架构有反馈连接?
A、循环神经网络
B、卷积神经网络
C、限制玻尔兹曼机
D、都不是
RNN循环神经网络的结构定义就是具有反馈层的,这样才成功实现了记忆功能。
CNN卷积神经网阔并不具备反馈,它本质是一种前馈的网络
而受限波尔兹曼机,它的结构和全连接网络一样,只不过内部计算的方式不同。
第二部分·填空题
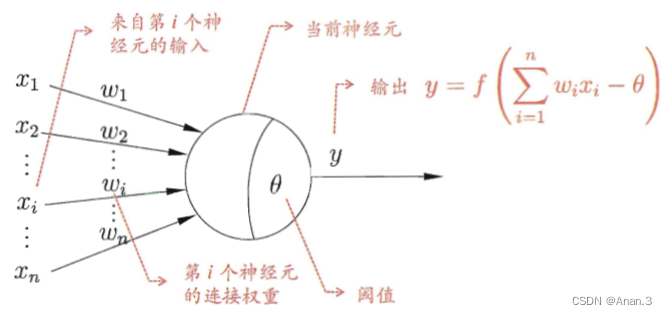
1.感知机只有 (输出神经层神经元) 进行激活函数处理,即只拥有一层功能神经元。
2.神经网络中最基本的成分是( 神经元模型)。
3.在具有n个单元的循环队列中,队满时共有(n-1) 个元素。
4.带表头结点的空循环双向链表的长度等于 (0) 。
5.(队列 ) 是被限定为只能在表的一端进行插入运算,在表的另一端进行删除运算的线性表。
第三部分·简答题
1.深度学习中有什么加快收敛?降低训练难度的方法有哪些?
残差,学习率、步长、动量
优化方法:预训练
2.请写出混淆矩阵,并写出查准率P和查全率R。
3.聚类算法的流程是什么,分步骤概述。
1.随机设置K个特征空间内的点作为初始的聚类中心
2.对于其他每个点计算到K个中心的距离,未知的点选择最近的一个聚类中心点作为标记类别
3.接着对着标记的聚类中心之后,重新计算出每个聚类的新中心点(平均值)
4.如果计算得出的新中心点与原中心点一样(质心不再移动),那么结束,否则重新进行第二步过程
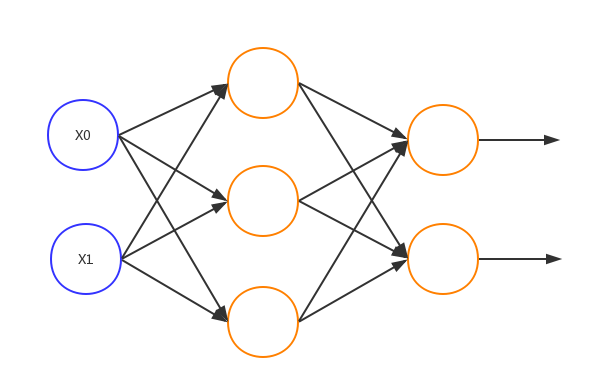
4.请画出三层神经网络的结构图。
输入层(最左侧),隐藏层(中间),输出层(最右侧)。
5.神经网络中会用到批量梯度下降吗?为什么会用随机梯度下降?
一般不用BGD。
1)BGD每次需要用到全量数据,计算量太大
2)引入随机因素,即便陷入局部极小,梯度也可能不为0,这样就有机会跳出局部极小继续搜索(可以作为跳出局部极小的一种方式,但也可能跳出全局最小。还有解决局部极小的方式:多组参数初始化、使用模拟退火技术)
6.监督学习,无监督学习的区别是什么?
监督学习一般有标签信息,而且是单步决策问题,比如分类问题。监督学习的样本一般是独立同分布的。
无监督学习没有任何标签信息,一般对应的是聚类问题。
7.深度学习中batch的大小对学习效果有何影响?
Batch 的选择,首先决定的是下降的方向。
如果数据集比较小,完全可以采用全数据集 ( Full Batch Learning )的形式,这样做至少有 2 个好处:其一,由全数据集确定的方向能够更好地代表样本总体,从而更准确地朝向极值所在的方向。
其二,由于不同权重的梯度值差别巨大,因此选取一个全局的学习率很困难。
Full Batch Learning 可以使用Rprop 只基于梯度符号并且针对性单独更新各权值。
8.卷积网络cnn中池化层的作用是什么?
减小图像尺寸,即数据降维,缓解过拟合,保持一定程度的旋转和平移不变性。
9.请写出顺序栈的栈空条件,栈满条件以及出栈进栈操作。
栈空的条件:s->top==-1;
栈满的条件:s->top==最大下标-1;
元素进栈操作:先将栈顶指针增1,然后将元素放在栈顶指针处。
出栈操作:先将栈顶指针处的元素取出,然后将栈顶指针减1。
10.如图所示的二叉树,请分别写出中序和后序遍历序列。
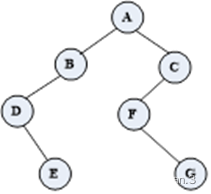
中序:DEBAFGC(左根右)
后序:EDBGFCA(左右根)
第四部分·编程题
1.用数组实现一个栈结构,包括出栈,入栈,获取栈内的元素个数,获取栈顶元素4个功能。
c语言
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAX 1000
typedef struct stack{
int ans[MAX];
int top;
}Stack;
//初始化栈
void InitStack(Stack *p){
p->top=0;
}
//判断栈满
bool StackFull (Stack *p) {
if (p->top<MAX)
return false;
else
return true;
}
//判断栈空
bool StackEmpty (Stack *p) {
if (p->top==0)
return true;
else
return false;
}
//入栈
int Push(Stack *p) {
int item;
printf("请输入要入栈的值:");
scanf("%d",&item);
if (StackFull(p))
printf("栈满,不能入栈");
else {
p->ans[p->top]=item;
p->top++;
}
}
//出栈
int Pop(Stack *p) {
if (StackEmpty(p)) {
printf("栈空,不能出栈");
return -1;
}
else
return p->ans[--p->top];
}
//获取栈内个数
int StackSize (Stack *p) {
if (p->top==0)
return 0;
else
return p->top;
}
//获得栈顶元素
int GetTop(Stack *p) {
return p->ans[p->top-1];
}
int main(){
Stack *p=(Stack *)malloc(sizeof(Stack));
InitStack(p);
int a;
while(1){
printf("请输入要进行的操作(0入栈/1出栈/2结束):");
scanf("%d",&a);
switch(a){
case 0:
Push(p);
break;
case 1:
Pop(p);
break;
case 2:
return 0;
break;
}
printf("栈内元素个数为:%d\n",StackSize(p));
printf("栈顶元素为:%d\n",GetTop(p));
}
return 0;
}
2.若 s 和 t 中每个字符出现的次数都相同,则称 s 和 t 互为字母异位词。现给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。假设字符串都是由26个小写英文字母组成,不包括其他元素。(一层for循环解决得满分,两层for循环解决得一半分数)
示例 1:
输入: s = “anagram”, t = “nagaram”
输出: true
示例 2:
输入: s = “rat”, t = “car”
输出: false
python
def f(a,b):
c={}
d={}
for i in a:
if i in c.keys():
c[i]+=1
else:
c[i]=1
for i in b:
if i in d.keys():
d[i]+=1
else:
d[i]=1
if d==c:
return True
else:
return False
a=input()
b=input()
print(f(a,b))
3.只调用numpy,编写一个三层神经网络,包含一个隐藏层。相关的神经元个数及权重可以自定义。激活函数选择Sigmoid,Tanh,Relu均可。
import numpy as np
def sigmoid(x):
return 1/(1+np.exp(-x))
def init_network():
network={}
network['w1']=np.array([[0.2,0.2,0.6],[0.1,0.1,0.8]])
network['b1']=np.array([0.5,0.6,0.7])
network['w2']=np.array([[0.1,0.9],[0.2,0.8],[0.3,0.7]])
network['b2']=np.array([0.5,0.5])
network['w3']=np.array([[0.1,0.9],[0.2,0.8]])
network['b3']=np.array([0.5,0.5])
return network
def forward(network,x):
w1,w2,w3=network['w1'],network['w2'],network['w3']
b1,b2,b3=network['b1'],network['b2'],network['b3']
#np.dot()矩阵
a1=np.dot(x,w1)+b1
z1=sigmoid(a1)
a2=np.dot(z1,w2)+b2
z2=sigmoid(a2)
a3=np.dot(z2,w3)+b3
y=a3
return y
network=init_network()
x=np.array([0.6,0.7])
y=forward(network,x)
print(y)