最近在看一本关于图像处理的书–《数字图像处理》,我的看书一般都会偏向教学书籍一点,能让新人都听懂,而且视频也比较全。看到其中 图像变换这块,跟我之前的文章《复杂情况下的二维码识别》里面的一些内容有关联,所以我准备在这里输出一篇文章来讲解一下我学到的知识,希望对你们有所帮助。
图像变换
首先要说的一点就是,我们这里的图像默认为简单的灰度图像,一个像素点占8比特,灰度等级是[0,255]。这也是为了方便我们理解文章内容。
我们这里主要讲解图像变换中的灰度变换,简单来说灰度变换就是一个函数,输入值是原图像的灰度值,输出值作为新图像的灰度值。不同类型的函数对图像的处理也是不一样的。可以处理一些环境过暗或者过亮的图像。来重现细节内容。如下所示
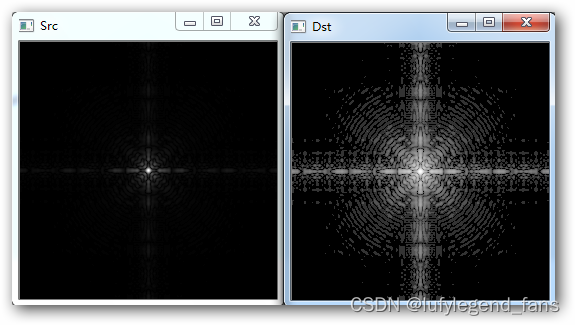
这里使用的是对数变换

但是这种图像变换需要入参,也就是我们需要对图像做出什么程度的变换。这就需要我们分析们的图像,变换我们的入参,不断的尝试才能得到一个满意的参数。当然现在我们可以使用机器学习来帮我们做这个步骤,设置一些反馈量,让电脑帮我们找到针对这幅图的最佳参数。
那有没有这样一种算法,会根据图像的总体亮暗自动调整,输出一个能让我们基本满意的图像!
直方图均衡化
直方图均衡化就是这样的算法,自动实现最佳参数的选取。
什么是直方图?
先让我们用大白话来讲解一下什么是直方图,将一个灰度图中各种灰度等级的像素点数量列出来。一般图像的像素点大小是8比特,也就是他的灰度等级是0-255。然后我们计算0灰度等级的像素个数,1灰度等级的像素个数…254灰度等级的像素个数,255灰度等级的像素个数。然后按照顺序列成一张表。这就是直方图。
当然只是直方图的其中一种表现方式,你也可以计算出每个灰度等级的像素数量占总像素数量的比重,这也就是归一化(这个计算过程叫做PDF,概率密度函数)。后面我们所说的直方图一般都是这个归一化的直方图。
公式推导
我们假设有这样一个函数T,输入像素r,输出像素s。有s=T( r );
根据概率论的基本结论,若已知原图的PDF和变换函数,且变换函数是连续的且在感兴趣的值域上是可微的,则有:
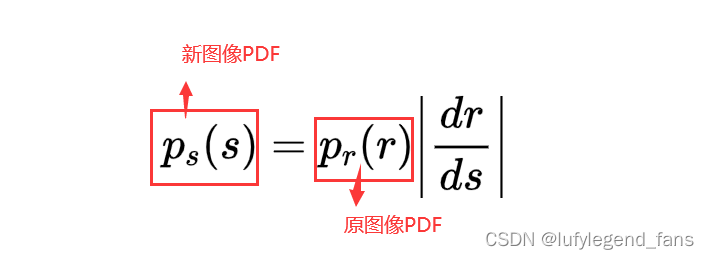
图像处理中的一个特别重要的变换函数是(tips:我也不知道这个公式是哪来的…)
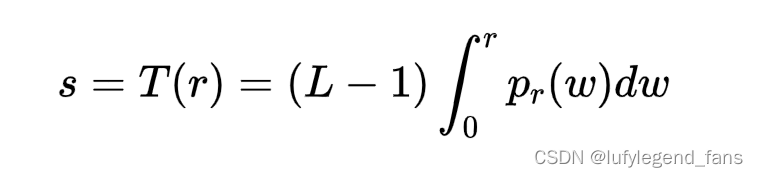
根据这个重要的变换函数我们就能推到:
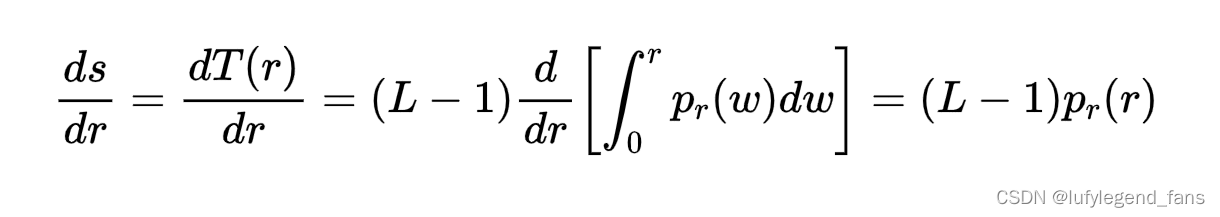
这样我们就能将这个结果带入概率论的基本结论中:
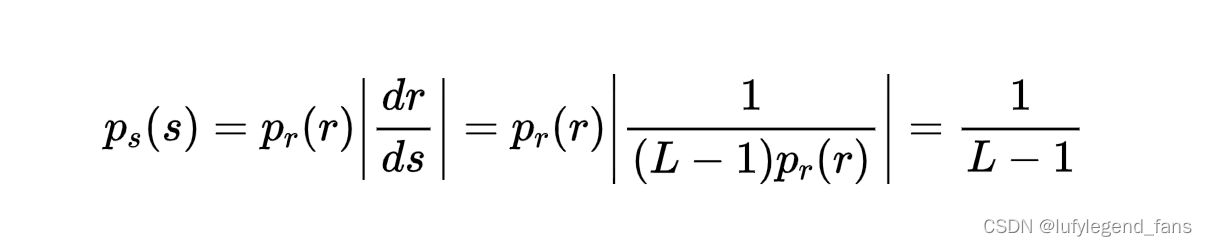
计算到这里我们惊讶的发现新图像的PDF尽然是一条平行与X轴的线,Y坐标值为1/(L-1)。这就代表所有的灰度等级在这副图像上出现的概率是一样的。这也就是全局直方图均衡化的原理。
不足之处
全局直方图均衡化,确实能显示某些类型图像的细节部分。但是全局直方图均衡化也有失效的时候,如下图所示,左图像为原图,我们能看到所有黑色方块中的重要细节。由于这些物体的灰度值太接近黑色方块的灰度,加之尺寸太小,因此使得全局直方图均衡化无法显示这种灰度细节。

局部直方图均衡化
上面一直在讨论全局的变换,因为像素是由基于整个图像的灰度分布的变换函数修改的。这种全局性方法适合于整体增强,但当目的是增强图像中的几个小区域的细节时,通常就会失败。所以我们要设计出基于像素邻域的灰度分布的变换函数。这个邻域的大小一般是3x3。上图中的右图就是局部直方图均衡化的结果。(具体的推导方式就不写了)
图像增强
基础推导
我们可以从图像的直方图中提取统计信息来用于增强图像。上面的推导过程中,我们一直将原图像看作连续函数,但其实图像是一个离散随机变量。然后通过直方图的统计量计算出均值
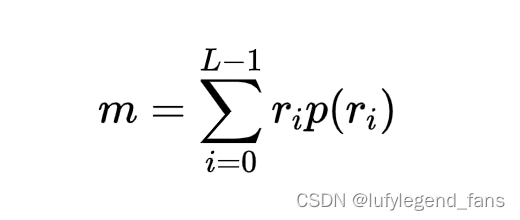
方差

均值是平均灰度的测度,而方差则是图像对比度的测度。这里我们需要对图像的邻域做处理,所以需要将上面两个公式转换成邻域均值和方差
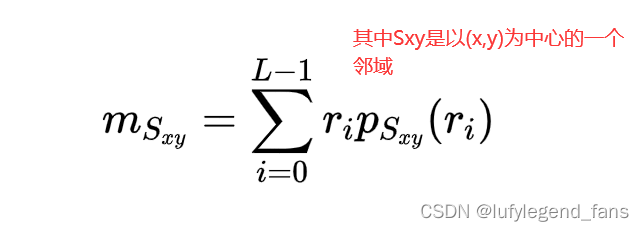
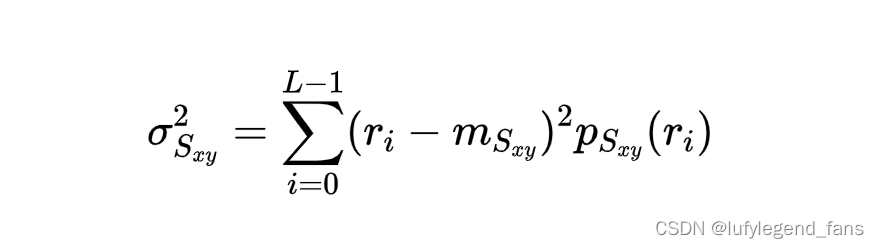
筛选像素
根据均值和方差,我们筛选出我们感兴趣的像素。粗略一点的筛选方式就是,感兴趣区域偏暗,所以全局灰度均值大于局部灰度均值。感兴趣区域灰度值比较接近,所以全局的对比度大于局部对比度。
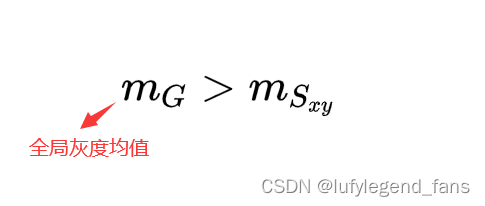

通过这种方法历遍图像,我们就能找到感兴趣区域的图像坐标。然后对这些坐标进行增强,又因为全局最大灰度值是228,感兴趣区域的最大灰度值是10,所以我们将感兴趣区域的灰度值增强22.8倍,向下取整就是22倍。这样我们对于图像的局部增强就完成了。
我们这里只是粗略的筛选我们的感兴趣区域,这样做其实会导致很多不是我么感兴趣的区域也被增强了,这是我们不想看到的。所以我们要优化我们的筛选条件。
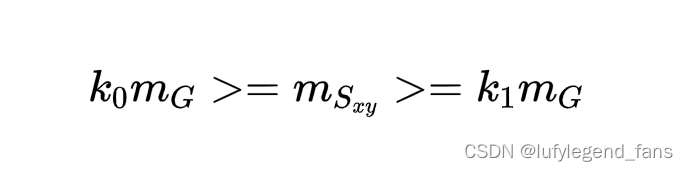
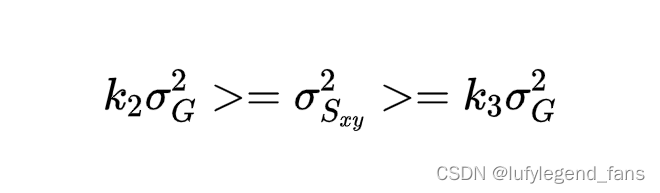
根据对图像均值和对比度的分析,我们决定设k0=0.1; k1=0; k2=0.1; k3=0。重新筛选像素点进行增强

写在结尾
这篇文章中的大部分内容都来自于《数字图像处理》这本书,我只是一个知识的搬运者,可能有些理解和想法是错误的,如果读者有不一样的想法,可以和我分享。天道酬勤,与君共勉!