#导入numpy
import numpy as np
#导入可视化工具matplotlib
import matplotlib.pyplot as plt
#生成一个-10到10之间,元素数为200的等差数列
x = np.linspace(-10,10,200)
#输入直线方程
y = -2*x + 3
#使用matplotlib绘制折线图
plt.plot(x,y,c='purple')
#图题设为“basic linear model”
plt.title('basic linear model')
#显示图像
plt.show()
#导入pandas
import pandas as pd
#用字典数据类型存储两个学生的年龄和身高
data = {'Age' : [14,18],
? ? ? ?'Height' : [165,175]}
#把字典转换为pandas数据框
data_frame = pd.DataFrame(data)
#检查一下是否成功
data_frame.head()

?#导入线性回归模型
from sklearn.linear_model import LinearRegression
#创建一个回归器,所有参数保持默认
reg = LinearRegression()
#把样本的年龄赋值给x,作为特征
x = data_frame['Age'].values.reshape(-1,1)
#样本身高赋值给y,作为标签
y = data_frame['Height']
#使用x,y训练线形回归模型
reg.fit(x,y)
#令z为10-20之间的等差数列,元素数为20
z = np.linspace(10,20,20)
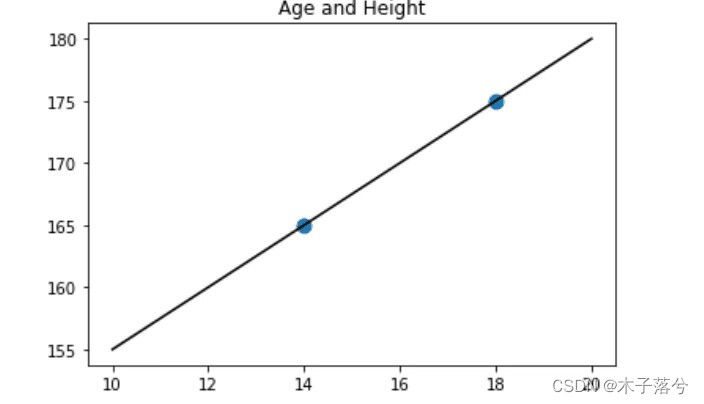
#将x和y用散点图的形式展现出来
plt.scatter(x,y,s=80)
#用直线绘制模型
plt.plot(z, reg.predict(z.reshape(-1,1)),c='k')
#设定图题为“Age and Height”
plt.title('Age and Height')
#显示图像
plt.show()
?
#打印模型中的coef_和intercept_属性
print(reg.coef_, reg.intercept_)
[2.5]? ?130.0
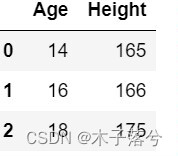
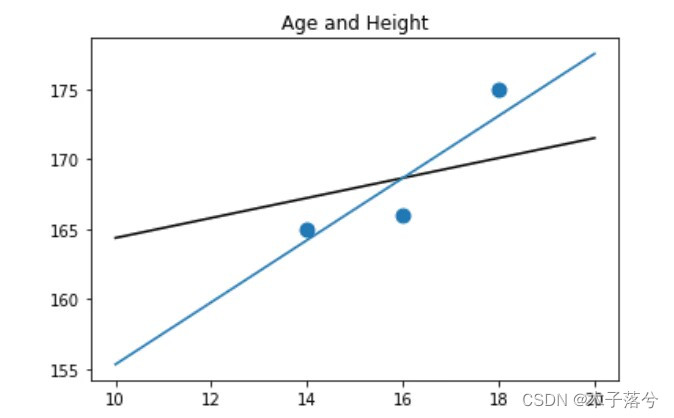
#用字典数据类型存储3个学生的年龄和身高
data2 = {'Age' : [14,16,18],
? ? ? ?'Height' : [165,166,175]}
#把字典转换为pandas数据框
data_frame2 = pd.DataFrame(data2)
#检查一下是否成功
data_frame2.head()
?#再次定义一个回归器reg2
reg2 = LinearRegression()
#把样本的年龄赋值给x
x2 = data_frame2['Age'].values.reshape(-1,1)
#样本身高赋值给y
y2 = data_frame2['Height']
#使用x,y训练线形回归模型
reg2.fit(x2,y2)
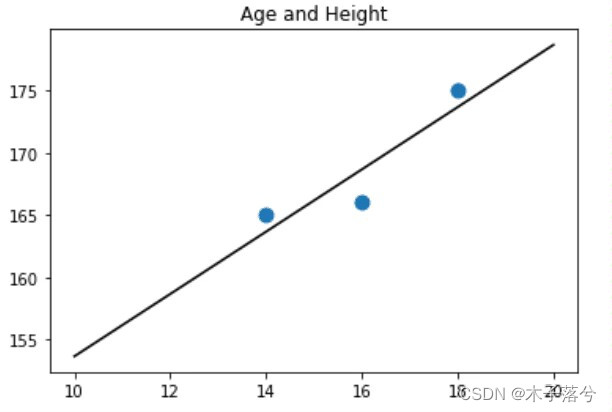
#将x2和y2用散点图的形式展现出来
plt.scatter(x2,y2,s=80)
#用直线绘制模型,继续使用之前生成的等差数列z
plt.plot(z, reg2.predict(z.reshape(-1,1)),c='k')
#设定图题为“Age and Height”
plt.title('Age and Height')
#显示图像
plt.show()
?
#查看reg2的斜率与截距
print(reg2.coef_,reg2.intercept_)
[2.5]? 128.66666666666669
#岭回归模型
from sklearn.linear_model import Ridge
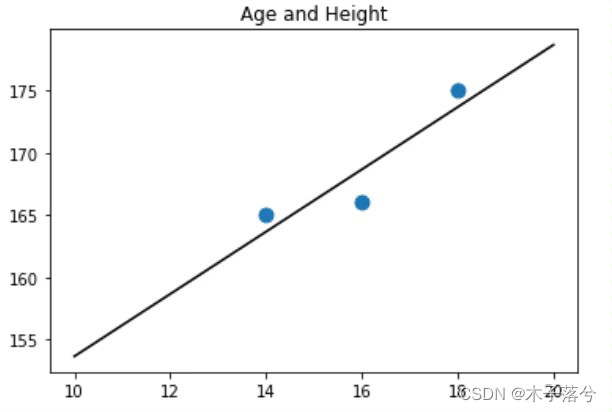
#使用岭回归对数据进行拟合
ridge = Ridge().fit(x2, y2)
#将x2和y2用散点图的形式展现出来
plt.scatter(x2,y2,s=80)
#用直线绘制模型,继续使用之前生成的等差数列z
plt.plot(z, ridge.predict(z.reshape(-1,1)),c='k')
#设定图题为“Age and Height”
plt.title('Age and Height')
#显示图像
plt.show()
?
#使用alpha为20的岭回归对数据进行拟合
ridge2 = Ridge(alpha=20).fit(x2, y2)
#将x2和y2用散点图的形式展现出来
plt.scatter(x2,y2,s=80)
#用直线绘制模型,继续使用之前生成的等差数列z
plt.plot(z, ridge2.predict(z.reshape(-1,1)),c='k')
#用直线绘制模型,继续使用之前生成的等差数列z
plt.plot(z, ridge.predict(z.reshape(-1,1)))
#设定图题为“Age and Height”
plt.title('Age and Height')
#显示图像
plt.show()
?#查看ridge的直线斜率与截距
print(ridge.coef_, ridge.intercept_)
#查看ridge2的直线斜率与截距
print(ridge2.coef_, ridge2.intercept_)
[2.22222222] 133.1111111111111
[0.71428571] 157.23809523809524