[人工智能]用于交通预测的时空交互动态图卷积网络

摘要

https://arxiv.org/abs/2205.08689
精确的交通预测对于城市交通控制、路线规划和流量检测都是至关重要的。虽然目前提出了许多时空分析方法，但在同步捕捉交通数据的时空依赖性方面仍有不足。此外，大多数方法都忽略了道路网络节点之间随着时间演变而产生的隐藏动态关联。我们提出了一种基于神经网络的时空交互动态图卷积网络(STIDGCN)来解决上述交通预测的挑战。具体而言，我们提出了一种交互式动态图卷积结构，该结构将交通数据按间隔分割，并通过交互式学习策略同步捕获分割后的交通数据的时空依赖性。交互式学习策略激励STIDGCN对长期预测有效。我们还提出了一个动态图卷积模块，通过一种新颖的动态图生成方法来捕获交通网络中动态变化的空间相关性。动态图生成方法基于先验知识和输入数据，生成动态图结构，可以挖掘道路网络中不可见的节点连接，模拟节点之间随时间的动态关联。在四个真实的交通流数据集上的大量实验表明，STIDGCN优于最先进的基线。

简介

借助从道路、出租车、私家车轨迹、公共交通交易记录等传感器收集到的海量城市交通数据，大交通数据分析已成为智慧城市发展[1]中交通规划、控制和状态评估不可或缺的一部分。交通预测是利用观测到的历史交通数据对城市动态进行预测，是流量控制、路线规划、流量检测等交通服务的关键。准确的交通预测有助于减少道路拥堵，促进交通路网的城市管理，甚至提高交通效率。

尽管在过去的几十年里，交通预测一直是一个活跃的研究热点，人们在这一领域做了大量的研究来提高预测性能，但它仍然面临着一些挑战。交通数据是具有复杂时间相关性和动态空间相关性的时空数据。城市交通数据作为一种时间序列数据，具有特定的周期性和趋势，如早晚高峰。有效地捕捉周期性和趋势需要能够准确捕捉产出和投入之间长期依赖关系的模型。因此，这些复杂的时间相关性使得长期预测交通数据变得困难。例如，当使用过去12时步的观测交通数据预测未来12时步的数据时，通常准确预测第9 -12时步的数据比预测第1 -3时步的数据要困难得多。如图1所示，由于路网交通流的错综复杂，交通数据的动态空间相关性也是多样化的。图1a显示，交通状况可以在空间上相互影响并动态变化。例如，某一路段发生意外，会影响邻近路段的交通状况。此外，同一路段上不同方向的车流也可能表现出不同的行为。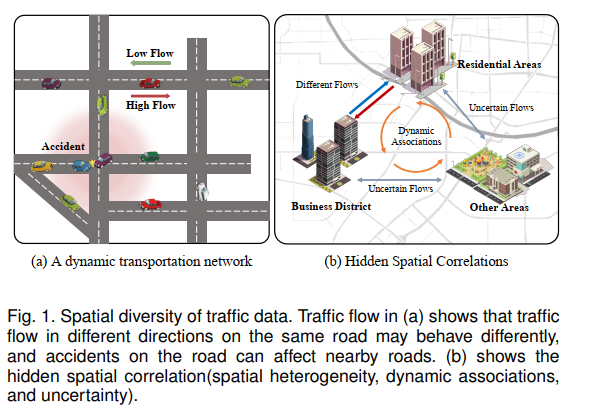
交通动态中还存在一些隐藏的空间相关性，这些相关性来源于空间异质性、动态关联和不确定性。这种隐含的空间相关性也给交通预测带来了挑战。如图1b所示，空间异质性意味着不同的区域(例如。(包括住宅区和商圈)的交通模式不同，因为它们有不同的特点，例如道路类型、道路宽度、公共交通指标等。动态关联是由流量产生的节点间的时变关联。这种关联可以从历史交通数据和路网结构中得到。不确定性是指事件对交通状况的影响，如天气变化、节假日和突发事件。

为了有效地捕捉时空相关性，采用了一些基于深度学习的方法。空间相关性和时间相关性在交通预测中得到了广泛的研究。如表1所示，一些方法分别捕获时间相关性和空间相关性，并将它们串联或并行组合。这些方法可能会削弱捕获的时空相关性，甚至放大一些不重要的特征。其他一些最近的方法试图通过将空间模块嵌入到时间模块中来同步捕获空间和时间依赖性，这对模型有积极的贡献。然而，这些方法中使用的时空模块在交通数据之间的时空信息交互学习方面受到限制，影响了模型对序列周期性和趋势的感知。

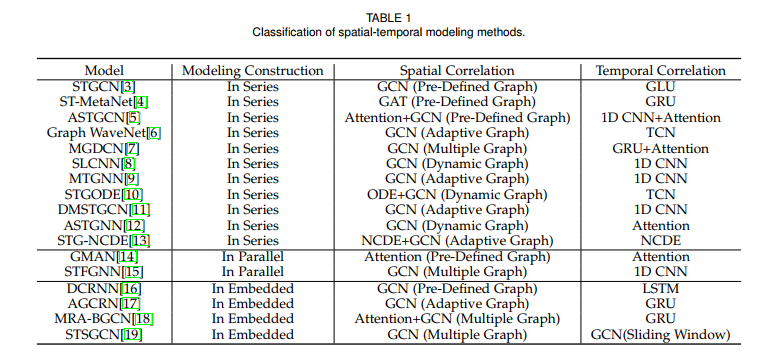
为了捕捉隐藏的空间相关性，许多当前的研究通过定义各种邻接矩阵来绘制更深层次的图结构。如表1所示，这些研究通过定义自适应邻接矩阵或组合多个邻接矩阵来捕获隐藏的空间相关性。然而，这些方法并没有充分利用历史交通数据。尽管自适应邻接矩阵可以发现图节点之间的隐式关系，从而增强模型对空间异质性的捕捉，但随着模型训练的停止，它将是固定的。它不能模拟图节点之间随时间变化的动态关联。因此，这些方法仍然不足以有效地捕获隐藏的空间相关性。利用历史流量数据和初始邻接矩阵可以进一步探讨节点间随时间的动态关联。

基于以上考虑，我们提出了一个时空交互动态图卷积神经网络(STIDGCN)来探讨输入数据与路网动态相关性之间的相互作用。我们设计了一个交互式动态图卷积网络来捕捉交通数据的时空依赖性。STIDGCN将图卷积模块嵌入到交互式学习结构中，可以同步捕获交通数据的时空相关性。该结构利用时间序列的趋势性，以间隔对序列进行划分。划分的子序列之间的交互学习探索了时空数据之间潜在的关联。为了有效地捕获隐藏的空间相关性，我们提出了一种动态图卷积网络，该网络通过动态图生成方法充分利用已有的先验知识(图结构、历史数据)。

这项工作的贡献概括如下:

• 提出了一种新的时空模型STIDGCN，该模型将图卷积嵌入到交互式学习结构中。它能够同步捕获时间和空间相关性。通过交互式学习结构和动态图卷积网络可以学习时空依赖性，从而实现有效的远程预测。

• 通过动态图生成方法，提出了一种动态图卷积网络。动态图由自适应和可学习邻接矩阵融合生成，其中自适应邻接矩阵发现空间异质性，可学习邻接矩阵模拟节点之间的动态关联。

• 在之前工作中的四个真实数据集上进行了大量实验。实验结果表明，与基线模型相比，我们的模型具有最先进的性能。

本文的其余部分组织如下:问题定义和相关工作在第2节中阐述。提出的方法将在第3节中详细说明。第四节给出了实验结果和分析。最后，在第5节中得出结论。

4 .实验结果及分析

为了评估STIDGCN的性能，我们在四个真实的高速公路交通流数据集上进行了大量的实验，并通过烧蚀实验验证了每个STIDGCN模块的功能。

4.1数据集

在我们的实验中，我们使用了四个真实的公共可用交通流数据集[19]，它们是PEMS03、PEMS04、PEMS07和PEMS08。所有四个数据集由Caltrans性能测量系统(pms)[43]每30秒实时收集一次。这些数据最终被聚合成5分钟的时间观察，因此一个小时有12个观察，我们的目标是预测下一个小时的交通数据。数据集细节如表2所示。实验中的图的邻接矩阵是根据这些真实交通路网中传感器之间的距离构造的。

4.2基本方法

我们将STIDGCN与15种基线方法进行了比较，结果如下:

• HA:历史平均使用历史数据的平均结果来预测未来的数据。

• VAR[44]:向量自回归是一个时间序列模型，它捕获了交通序列的时间相关性。

• SVR[45]:支持向量回归是一种机器学习方法，使用支持向量机对流量序列进行回归。

• LSTM[46]:长短期记忆是一种基于神经网络的模型，可以有效地捕获时间序列的相关性。

• TCN[30]:时序卷积神经网络通过叠加因果扩张卷积实现，有效捕获时间序列相关性。

• DCRNN[16]:扩散卷积循环神经网络(Diffusion Convolutional recurtional Neural Network)是一种结合了扩散GCN和GRU的编码器-解码器结构，用于捕获交通数据的时空依赖性。

• STGCN[3]:时空图卷积网络(Spatial-Temporal Graph Convolutional Network)将光谱GCN与一维卷积相结合，以捕获时空依赖性。

• ASTGCN[5]:基于注意力的时空图卷积网络通过分别设计空间和时间注意机制来捕获时空依赖性。

• Graph WaveNet [6]: Graph WaveNet将门控TCN与空间GCN相结合，提出了一种自适应邻接矩阵来学习动态空间相关性。

• AGCRN[17]:自适应图卷积循环网络是一种使用自适应图结构将GCN和GRU结合起来的模型。

• STSGCN[19]:时空同步图卷积网络是一种GCN模型，它构建多个局部时空图以同步捕获时空依赖性。

• STFGNN[15]:时空融合图神经网络通过对生成的时空图执行融合操作，有效地学习隐藏的相关性。

• ASTGNN[12]:基于注意力的时空图神经网络是一个自注意流量预测模型，它结合了时间趋势自注意机制和动态GCN。

• SCINet[31]:样本卷积和交互网络使用交互卷积结构，允许序列数据的多分辨率处理，并扩展卷积操作的接受域。

• STG-NCDE[13]:时空图神经控制微分方程利用时空ncde处理交通数据，是一种受控微分方程方法。

4.3设置

实验使用的所有数据集按照6:2:2的比例分为训练集、验证集和测试集。在将数据集提供给网络之前，应用z分数归一化来标准化数据集。对于缺失的流量数据，我们将其屏蔽，即不考虑这些缺失的数据(值为0)。我们使用过去一小时内12个连续时间步的数据来预测下一小时未来12个连续时间步的数据。

实验在一台Intel? Xeon? Gold 6230 CPU @ 2.10GHz和一台NVIDIA Tesla V100 GPU卡的计算机环境下进行。我们使用Ranger优化器[47]训练STIDGCN，初始学习率设置为0.001。批大小设置为64，训练周期为500，我们设置了早期停止机制。该模型在大约第300个纪元时收敛到结束。

我们选择了三个标准指标来评价所有方法的性能，分别是平均绝对误差(MAE)、平均绝对误差(MAPE)和均方根误差(RMSE)，定义如下:
$$MAE=\frac{1}{N}\sum _{i=1}^N\left|Y_i?{\hat{Y}}_i\right|\text{\hspace{1em}(14)}$$
$$MAPE=\frac{100\%}{N}\sum _{i=1}^N\left|\frac{Y_i?{\hat{Y}}_i}{Y_i}\right|\text{\hspace{1em}(15)}$$
$$RMSE=\sqrt{\frac{1}{N}\sum _{i=1}^N{\left(Y_i?{\hat{Y}}_i\right)}^2}\text{\hspace{1em}(16)}$$
其中N为样本数，$Y_i$为基础真理，${\hat{Y}}_i$为预测值。

4.4结果比较与分析

表3显示了STIDGCN在四组真实交通流数据测试集上的下一个小时(12时间步)的预测结果和比较模型。我们提出的STIDGCN在这四个流量数据集上的性能优于所有基线方法，除了PEMS03和PEMS04中的MAPE度量，它分别略差于图波网和SCINet。STIDGCN在PEMS07和PEMS08上，结果有更明显的改善。在PEMS07中，STIDGCN在MAE、RMSE和MAPE方面分别提高了6.1%、4.7%和5.0%。在PEMS08中，STIDGCN在MAE、RMSE和MAPE方面分别提高了6.5%、2.1%和3.7%。

表3的结果表明，统计方法(HA,VAR)、传统机器学习方法(SVR)、LSTM和TCN的性能较差，因为这些模型只考虑时间相关性，而忽略了交通数据中复杂的空间相关性。由于同时考虑了时空相关性，以STGCN和DCRNN为代表的时空GCN模型性能较好。此外，基于注意机制的模型(ASTGCN,ASTGNN)也表现良好，因为注意机制可以捕获长序列的时间相关性。图波网的性能甚至优于最近提出的一些模型(STFGNN, STG-NCDE)。图波网是将扩散GCN嵌入TCN的一种方法，具有很好的时间相关性捕获能力。这种紧凑的依赖性捕获接近于时空特征的同步捕获。尽管STSGCN使用同步方法来捕获时空特征，但它使用一个简单的滑动窗口来捕获时间相关性。这说明STSGCN忽略了时间相关性的捕获，即使在有效捕获空间相关性的情况下，其整体性能也不是很好。值得注意的是，即使不考虑空间相关性，SCINet也能取得良好的性能。它还展示了交互式学习的有效性和交通数据空间建模的重要性。NCDE作为一种新的深度学习模型，尽管取得了良好的效果，但由于其对时空特征的捕获是串联的，因此其性能不如STIDGCN。我们提出的STIDGCN使用交互式学习策略来同步捕获相关性。其DGCN模块可以探索路网中不可见的节点连接，捕捉隐藏的空间相关性，并模拟节点间随时间动态关联的生成。

图4显示了随着预测时间范围的增加，模型的一部分在四个交通数据集上的MAE、RMSE和MAPE的变化情况。随着预测水平的增加，预测难度也会发生变化;MAE、RMSE和MAPE将继续增加。我们提出的STIDGCN使用交互式学习策略，其中序列学习彼此的时空特征，以获得长期预测能力。如图4所示，基于注意机制的STIDGCN优于ASTGNN，即使是在长期预测方面。

4.5消融研究

为了进一步评估STIDGCN的哪些组分是影响模型结果的关键组分，我们在PEMS04和PEMS08数据集上进行了烧蚀实验。我们设计了6个STIDGCN变体，具体如下:

• w/o GCN:在STIDGCN的基础上，去掉扩散GCN模块。

• w/o DGCN:在STIDGCN的基础上，将DGCN模块替换为普通扩散GCN。输入到GCN的邻接矩阵是预定义的初始邻接矩阵。

• w/o Conv:在STIDGCN的基础上，从交互学习结构中去掉1D卷积模块。

• w/o交互:在STIDGCN的基础上，将交互学习结构替换为TCN，并与动态卷积模块串联。TCN设置为6层卷积，特征通道数为64。

• w/o Apt Adj:在STIDGCN的基础上，去除了DGCN模块的自适应邻接矩阵。将输入图生成器的邻接矩阵替换为预先定义的初始邻接矩阵。

• w/o学习Adj:在STIDGCN的基础上，去掉图生成器结构，保留自适应邻接矩阵，并在DGCN模块中将融合GCN改为扩散GCN。

消融实验结果如图5所示。这些组件对模型整体的影响在PEMS04和PEMS08数据集上的分布基本相似。我们还比较了消融实验中的ASTGNN。首先，GCN对于STIDGCN至关重要，其次，我们提出的IDGCN模块对于整体模型性能的提高至关重要。用于扩展感知域的一维卷积是交互式学习结构的重要组成部分，烧蚀实验表明，它能显著提高模型性能。用TCN替代交互学习结构后，模型性能下降，而ASTGNN的综合性能优于STIDGCN。验证了在交互器中同步特征捕获比在TCN或ASTGNN等序列中捕获更有效。此外，我们对DGCN模块内定义的两个邻接矩阵进行了消融研究，图5显示自适应邻接矩阵对模型至关重要。可学习邻接矩阵也发挥了重要作用，它与自适应邻接矩阵协同生成动态邻接矩阵。如图5所示，当STIDGCN去除了动态邻接矩阵时，ASTGNN的性能优于STIDGCN。说明了动态邻接矩阵用于图卷积的必要性。动态邻接矩阵允许图卷积更好地捕捉交通数据中隐藏的空间相关性。因此，我们提出的两个核心结构(交互式学习和动态图卷积)是有效的。

4.6不同结构配置的影响

为了进一步研究超参数设置和模型结构设置的影响，我们在PEMS08数据集上进行了实验。STIDGCN不采用重复堆叠模块的形式来捕获特征，因此与模型结构相关的唯一超参数是特征通道的数量。如图6所示，特征通道的数量具体影响STIDGCN。STIDGCN的性能不会随着特征通道数量的增加而持续提高。STIDGCN的性能在特征通道数量增加到特定值时也趋于平稳。当特征通道范围为64 ~ 80时，STIDGCN性能最好。然而，随着特征通道数量的增加，模型参数增多，推理时间变长。因此，最终选取STIDGCN的特征通道数为64个。

此外，我们对互动学习结构中的子模块做了一些修改，以证明目前的结构是最合理的。交互式学习结构由四个独立的卷积模块和一个权值共享的DGCN模块组成。卷积模块用于提取当前序列中不同时间步之间的相关性，拓宽了交互式学习体系结构中模型的接受域。同时，权重共享DGCN模块可以交互式学习不同序列的空间相关性。我们对IDGCN模块做了以下修改:

• IDGCN Conv×1:将交互式学习结构中的4个独立的卷积模块替换为一个权值共享的卷积模块。

• IDGCN DGCN×2:交互学习结构中的权重共享DGCN模块被2个独立的DGCN模块取代。两个独立的DGCN模块分别用于在两个交互学习会话期间捕获序列的空间相关性。

• IDGCN DGCN×4:交互学习结构中的权重共享DGCN模块被4个独立的DGCN模块取代。4个DGCN模块分别在两个交互学习过程中捕获序列的空间相关性。

• IDGCN Interaction×1:将交互学习结构中的交互学习个数由2个改为1个，即去掉2个卷积运算和1个图卷积运算。

• IDGCN Interaction×4:将交互学习结构中的交互学习个数由2个改为4个，即IDGCN模块中的交互学习操作重复两次。

如表4所示，结构变化影响STIDGCN。表4的结果表明，权值共享卷积模块并不比单独卷积模块更有效。DGCN模块性能相反;增加DGCN模块并不会带来更好的性能。权重分担的DGCN模块相当于交互学习中DGCN模块的堆叠，使STIDGCN在空间项上有更大的感受野，使节点与更远的节点产生关联。单独的DGCN模块不能提供共享的接收场，可能导致模型性能较差。STIDGCN使用同步策略来捕获交互式学习结构中的时空依赖性。因此，减少交互学习的数量意味着减少对时空依赖性的捕获，这种操作无疑会导致STIDGCN的性能变差。实验表明，两种交互学习方法足以对特征进行拟合，而在IDGCN模块中增加交互学习操作会导致特征拟合能力下降。

4.7计算时间

在这一部分中，我们比较了STIDGCN与表5中PEMS08数据集上的部分基线模型的计算成本。STIDGCN性能优异，计算成本低。与ASTGNN和STGNCDE等其他最先进的基线相比，STIDGCN在显著降低计算成本的同时实现了更好的性能。虽然ASTGNN具有紧急性能，但其处理数据的方式是自回归的，计算成本较高。图波采用并行数据处理，模型轻量化，计算成本低。虽然SCINet的计算成本最低，但在获取空间相关性方面存在不足。STIDGCN的计算成本主要来自于其交互学习中的动态图卷积结构。STIDGCN以非自回归的方式并行处理数据，提高了模型的效率。

结论

在本文中，我们提出了一个使用交互式学习策略的动态图生成模型STIDGCN。具体来说，我们将动态GCN模块嵌入到交互式学习结构中，以同步捕获时空依赖性。交互式学习策略的应用场景是具有一定周期性和趋势性的时间序列预测。我们提出了一个DGCN模块来模拟动态空间相关性，即使用输入的时空信息生成动态图结构，并与预先定义的初始邻接矩阵协同工作。DGCN模块探索道路网络中不可见的节点连接，以捕获隐藏的空间相关性，并模拟节点之间随时间产生的动态相关性。在四个真实数据集上的实验表明，同步学习和动态图形生成对于时空预测是必不可少的。我们提出的模型优于最先进的基线。在交互学习中，特征学习在个体序列中均匀分布。然而，数据之间的相关性并不总是均匀分布的。因此，我们认为在互动学习中使用注意机制是一个很好的改进方案。