[人工智能] NNDL 实验六卷积神经网络（1）卷积

受生物学上感受野机制的启发而提出。
一般是由卷积层、汇聚层和全连接层交叉堆叠而成的前馈神经网络
有三个结构上的特性：局部连接、权重共享、汇聚。
具有一定程度上的平移、缩放和旋转不变性。
和前馈神经网络相比，卷积神经网络的参数更少。
主要应用在图像和视频分析的任务上，其准确率一般也远远超出了其他的神经网络模型。
近年来卷积神经网络也广泛地应用到自然语言处理、推荐系统等领域。

5.1 卷积?

5.1.1 二维卷积运算

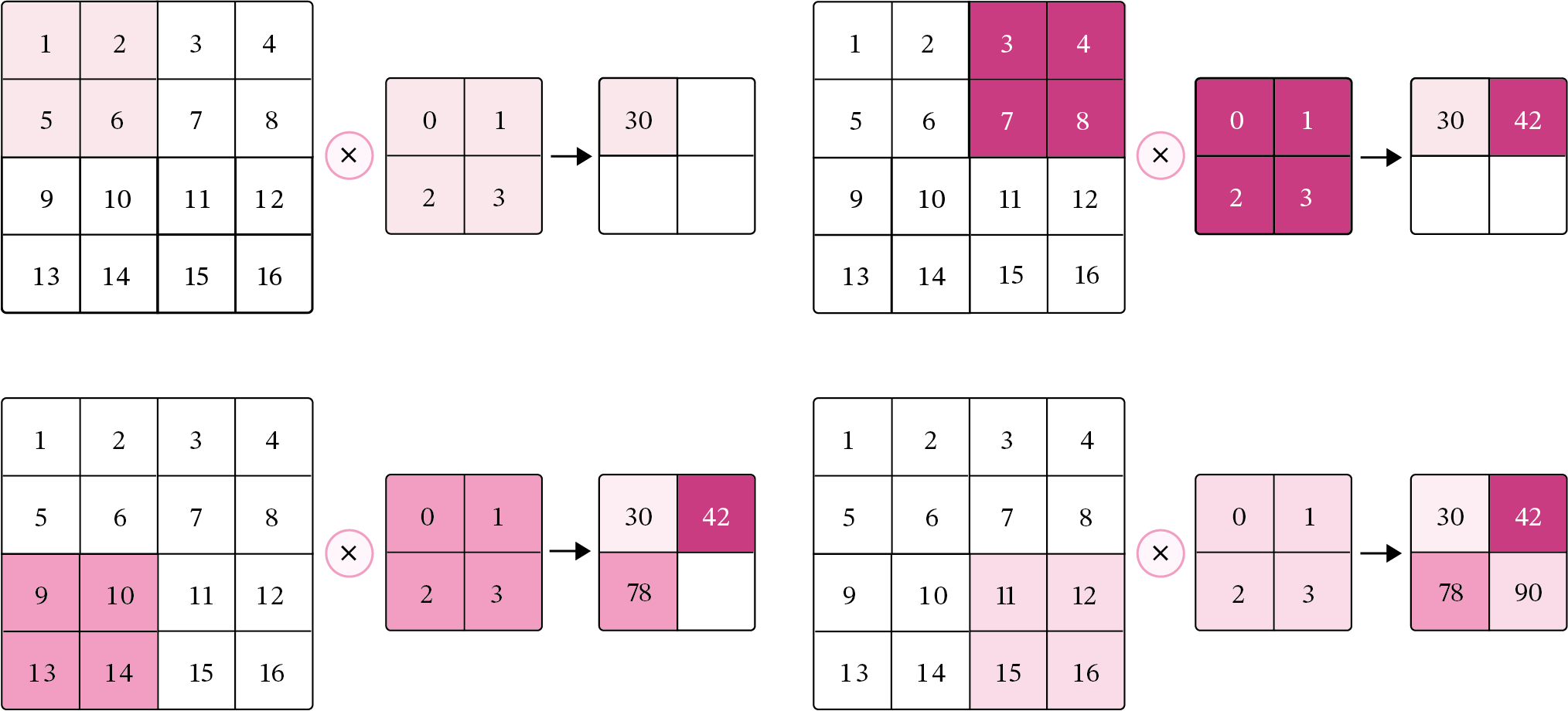
? ? ? ?在机器学习和图像处理领域，卷积的主要功能是在一个图像（或特征图）上滑动一个卷积核，通过卷积操作得到一组新的特征。在计算卷积的过程中，需要进行卷积核的翻转，而这也会带来一些不必要的操作和开销。因此，在具体实现上，一般会以数学中的互相关运算来代替卷积。
? ? ? ? 在神经网络中，卷积运算的主要作用是抽取特征，卷积核是否进行翻转并不会影响其特征抽取的能力。特别是当卷积核是可学习的参数时，卷积和互相关在能力上是等价的。因此，很多时候，为方便起见，会直接用互相关来代替卷积。

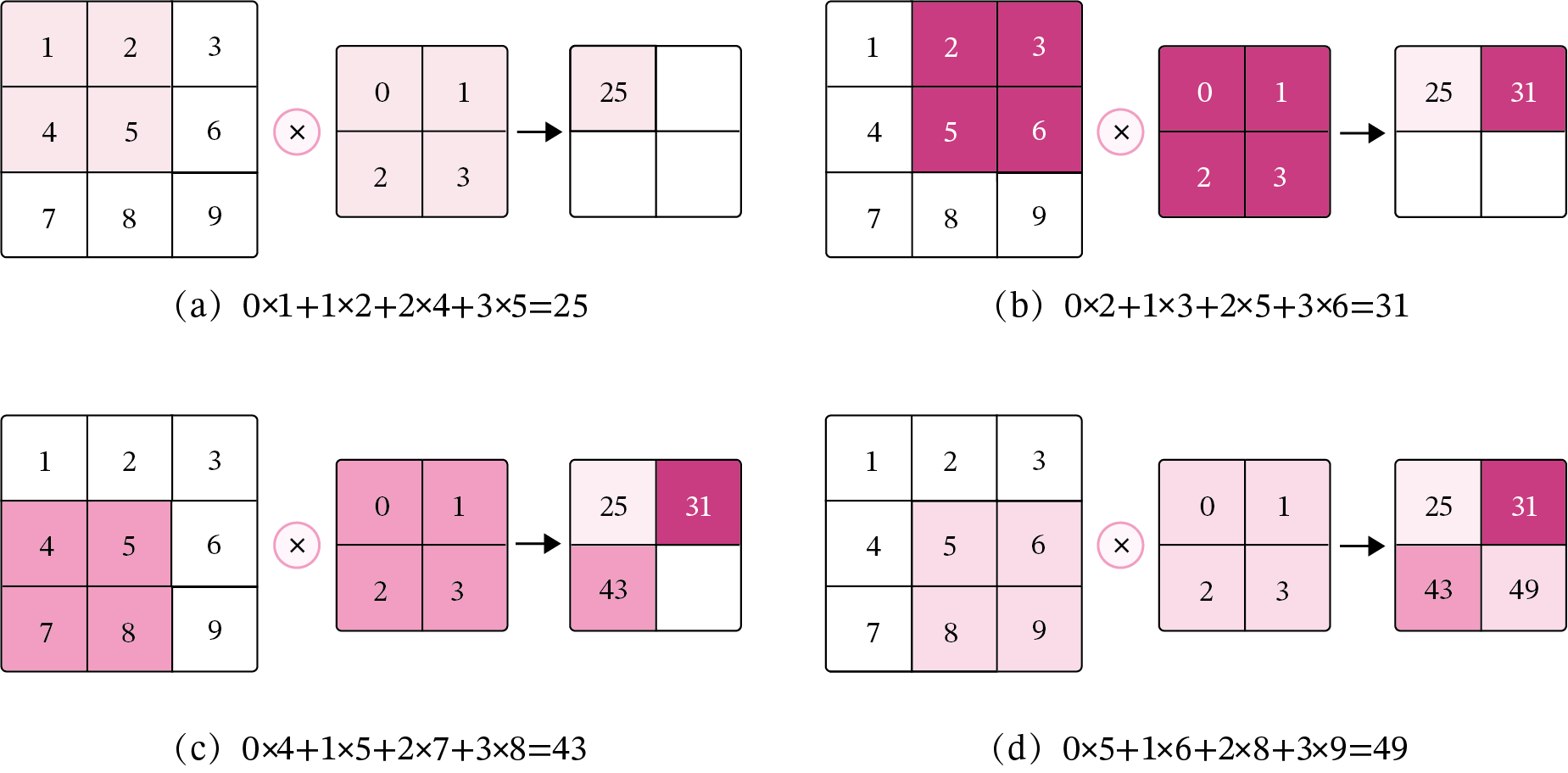
5.1.2 二维卷积算子

? ? ?在本节后面的实现中，算子都继承torch.nn.Module，并使用支持反向传播的torch.nn.Parameter函数进行实现，允许梯度下降，这样我们就可以不用手工写backword()的代码实现。

【使用pytorch实现自定义二维卷积算子】

代码如下：

import torch#导入包
class Conv2D(torch.nn.Module):#继承torch.nn.Module下的二维卷积算子
    def __init__(self, kernel_size, weight_attr=torch.tensor([[0., 1.],[2., 3.]])):#类初始化，初始化权重属性为默认值
        super(Conv2D, self).__init__()#继承torch.nn.Module中的Conv2D卷积算子
        self.weight = torch.nn.Parameter(weight_attr)
        #torch.nn.Parameter将一个不可训练的类型为Tensor的参数转化为可训练的类型为parameter的参数，并将这个参数绑定到module里面，成为module中可训练的参数。
        self.weight.reshape([kernel_size,kernel_size])#将卷积核大小改为kernel_size*kernel_size
    def forward(self, X):#定义前向传播
        """
        输入：
            - X：输入矩阵，shape=[B, M, N]，B为样本数量
        输出：
            - output：输出矩阵
        """
        u, v = self.weight.shape#得到输入形状大小
        output = torch.zeros([X.shape[0], X.shape[1] - u + 1, X.shape[2] - v + 1])#初始化输出矩阵
        for i in range(output.shape[1]):
            for j in range(output.shape[2]):
                output[:, i, j] = torch.sum(X[:, i:i+u, j:j+v]*self.weight, axis=[1,2])#进行卷积
        return output

# 随机构造一个二维输入矩阵
torch.manual_seed(100)#定义随机种子
inputs = torch.tensor([[[1.,2.,3.],[4.,5.,6.],[7.,8.,9.]]])#初始化输入
kernel = torch.tensor([[0.,1.],[2.,3.]])#初始化kernel即weight_attr
conv2d = Conv2D(kernel_size=2)#传入kernel_size参数
outputs = conv2d(inputs)#测试二维卷积算子
print("input:\n {}, \nuse kernel:\n {}\noutput:\n {}".format(inputs,kernel, outputs))#输出结果。

运行结果：

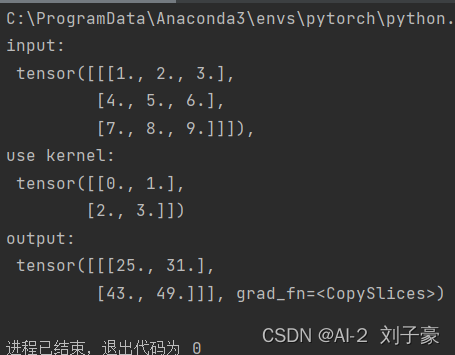5.1.3 二维卷积的参数量和计算量

? ? ? ?随着隐藏层神经元数量的变多以及层数的加深，使用全连接前馈网络处理图像数据时，参数量会急剧增加。如果使用卷积进行图像处理，相较于全连接前馈网络，参数量少了非常多。

5.1.3.1 参数量

1、卷积层的参数量

其中表示Cout输出通道数，Cin表示输入通道数，kw表示卷积核宽，kh表示卷积核高。 kw*kh*Cin括号内的表示一个卷积核的权重数量，+1表示bias，括号表示一个卷积核的参数量，Cout表示该层有Cout个卷积核。
2、全连接层的参数量?

其中表示Nout表示输出的权重数量，Nin表示输入的特征向量的权重，+1表示偏置。?

5.1.3.2 计算量

1、卷积层的FLOPs

?FLOPs是英文floating point operations的缩写，表示浮点运算量，中括号内的值表示卷积操作计算出feature map中一个点所需要的运算量（乘法和加法），kw*kh*Cin表示一次卷积操作中的乘法运算量，kw*kh*Cin-1表示一次卷积操作中的加法运算量，+ 1 表示bias，W和H分别表示feature map的长和宽，Coutwh表示feature map的所有元素数。
2、全连接层的FLOPs

其中In表示乘法运算量，In-1表示加法运算量，+1表示偏置。?

5.1.4 感受野

? ? ? ?在卷积神经网络中，感受野（Receptive Field）的定义是卷积神经网络每一层输出的特征图（feature map）上的像素点在输入图片上映射的区域大小。再通俗点的解释是，特征图上的一个点对应输入图上的区域。每个位置均会对相应神经元的激活产生影响，但并不是所有位置的贡献都相等。这种歧视就是有效感受野ERF，它是神经网络内在属性，当结构确定的时候，有效感受野的相关特性也就是确定的。两个神经元即使感受野大小一样，网络结构不同，有效感受野特性也会不同。

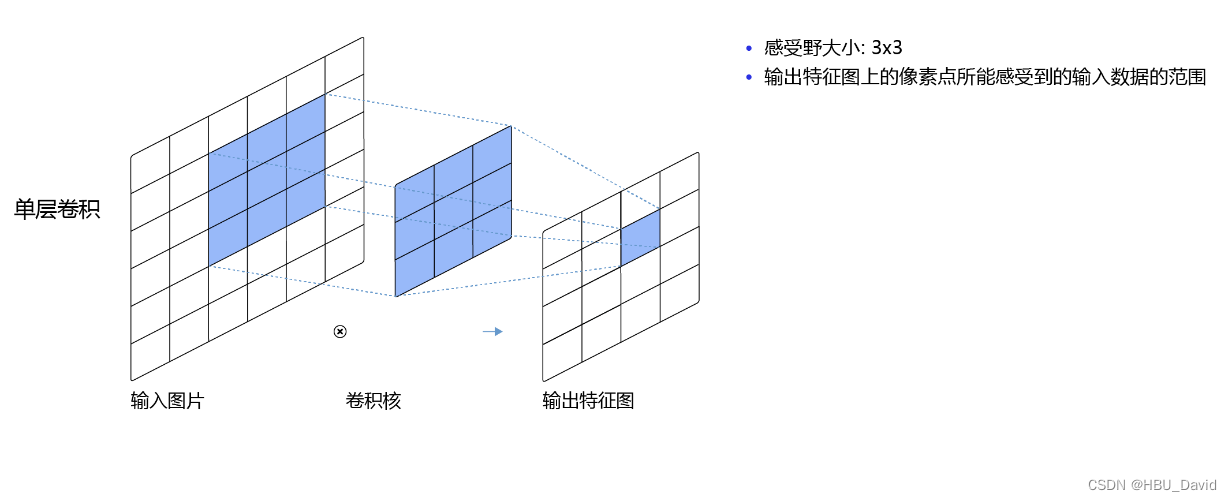
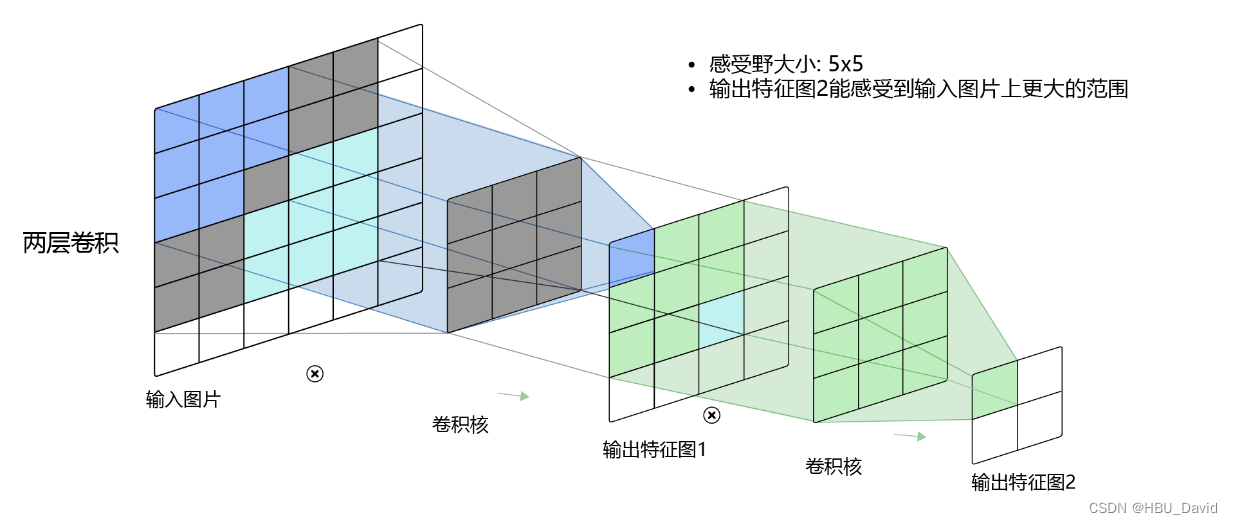
5.1.5 卷积的变种

5.1.5.1 步长（Stride）

Size为3的卷积核，如果step为1，那么相邻步感受野之间就会有重复区域，重复区域是两列的数据；如果step为2，那么相邻感受野的重复区域会更少；如果step为3，那么相邻感受野之间没有重复区域；如果step大于3，那么相邻步感受野之间会有一道大小为1的缝隙，从某种程度来说，这样就遗漏了原图的信息，直观上理解是不好的。

另外，当卷积核step为1时，输出矩阵Size会和输入矩阵Size保持一致（加padding填充周围中后）；而卷积核step为2时，由于跨步会导致输出矩阵Size降低为输入矩阵Size的一半。由此会产生一种类似“池化”的效果，利用这一特性可以代替池化层。

Stride的作用：是成倍缩小尺寸，而这个参数的值就是缩小的具体倍数，比如步幅为2，输出就是输入的1/2；步幅为3，输出就是输入的1/3。以此类推。

5.1.5.2 零填充（Zero Padding）

进行零填充（Zero Padding）的原因：
一：卷积的时候，希望图像大小不发生变化；
二：有的时候可能原始图像是除不尽的，如果不填充的话，余的像素就直接丢弃了，这样信息可能会丢失。那为了防止信息丢失，我们做一个填充。

5.1.6 带步长和零填充的二维卷积算子

【使用pytorch实现自定义带步长和零填充的二维卷积算子】

代码如下：

import torch
import torch.nn as nn
import torch.nn
import numpy as np


class Conv2D(nn.Module):
    def __init__(self, kernel_size,stride=1, padding=0):
        super(Conv2D, self).__init__()
        w = torch.tensor(np.array([[0., 1., 2.], [3., 4. ,5.],[6.,7.,8.]], dtype='float32').reshape([kernel_size, kernel_size]))
        self.weight = torch.nn.Parameter(w, requires_grad=True)
        self.stride = stride
        self.padding = padding

    def forward(self, X):
        # 零填充
        new_X = torch.zeros([X.shape[0], X.shape[1] + 2 * self.padding, X.shape[2] + 2 * self.padding])
        new_X[:, self.padding:X.shape[1] + self.padding, self.padding:X.shape[2] + self.padding] = X
        u, v = self.weight.shape
        output_w = (new_X.shape[1] - u) // self.stride + 1
        output_h = (new_X.shape[2] - v) // self.stride + 1
        output = torch.zeros([X.shape[0], output_w, output_h])
        for i in range(0, output.shape[1]):
            for j in range(0, output.shape[2]):
                output[:, i, j] = torch.sum(
                    new_X[:, self.stride * i:self.stride * i + u, self.stride * j:self.stride * j + v] * self.weight,
                    axis=[1, 2])
        return output


inputs = torch.randn(size=[2, 8, 8])
conv2d_padding = Conv2D(kernel_size=3, padding=1)
outputs = conv2d_padding(inputs)
print("When kernel_size=3, padding=1 stride=1, input's shape: {}, output's shape: {}".format(inputs.shape, outputs.shape))
conv2d_stride = Conv2D(kernel_size=3, stride=2, padding=1)
outputs = conv2d_stride(inputs)
print("When kernel_size=3, padding=1 stride=2, input's shape: {}, output's shape: {}".format(inputs.shape, outputs.shape))

运行结果：

? ? ? ?从输出结果看出，使用3×3大小卷积，padding为1，当stride=1时，模型的输出特征图与输入特征图保持一致；当stride=2时，模型的输出特征图的宽和高都缩小一倍。

5.1.7 使用卷积运算完成图像边缘检测任务

【使用pytorch实现图像边缘检测】

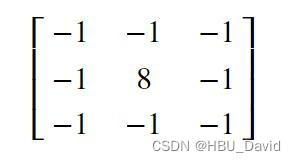代码如下：

import torch
import torch.nn as nn
import torch.nn
import numpy as np


class Conv2D(nn.Module):
    def __init__(self, kernel_size,stride=1, padding=0):
        super(Conv2D, self).__init__()
        # 设置卷积核参数
        w = np.array([[-1, -1, -1], [-1, 8, -1], [-1, -1, -1]], dtype='float32').reshape((3,3))
        w=torch.from_numpy(w)
        self.weight = torch.nn.Parameter(w, requires_grad=True)
        self.stride = stride
        self.padding = padding

    def forward(self, X):
        # 零填充
        new_X = torch.zeros([X.shape[0], X.shape[1] + 2 * self.padding, X.shape[2] + 2 * self.padding])
        new_X[:, self.padding:X.shape[1] + self.padding, self.padding:X.shape[2] + self.padding] = X
        u, v = self.weight.shape
        output_w = (new_X.shape[1] - u) // self.stride + 1
        output_h = (new_X.shape[2] - v) // self.stride + 1
        output = torch.zeros([X.shape[0], output_w, output_h])
        for i in range(0, output.shape[1]):
            for j in range(0, output.shape[2]):
                output[:, i, j] = torch.sum(
                    new_X[:, self.stride * i:self.stride * i + u, self.stride * j:self.stride * j + v] * self.weight,
                    axis=[1, 2])
        return output

import matplotlib.pyplot as plt
from PIL import Image
# 读取图片
img = Image.open('D:\刘子豪\应用程序\pycharm\python项目\liu\OIP-C.jpg').convert('L')
img = np.array(img, dtype='float32')
im = torch.from_numpy(img.reshape((img.shape[0],img.shape[1])))

# 创建卷积算子，卷积核大小为3x3，并使用上面的设置好的数值作为卷积核权重的初始化参数
conv = Conv2D(kernel_size=3, stride=1, padding=0)

# 将读入的图片转化为float32类型的numpy.ndarray
inputs = np.array(im).astype('float32')
print("bf as_tensor, inputs:",inputs)
# 将图片转为Tensor
inputs = torch.as_tensor(inputs)
print("bf unsqueeze, inputs:",inputs)
inputs = torch.unsqueeze(inputs, axis=0)
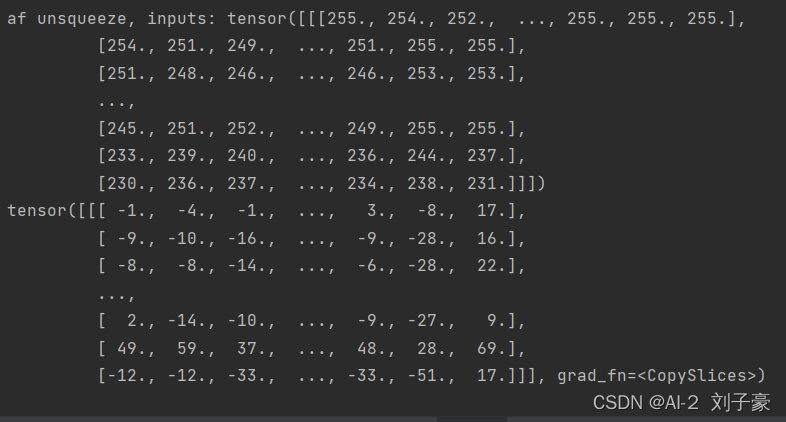
print("af unsqueeze, inputs:",inputs)
outputs = conv(inputs)
print(outputs)
# outputs = outputs.data.squeeze().numpy()
# # 可视化结果
plt.subplot(121).set_title('input image', fontsize=15)
plt.imshow(img.astype('uint8'),cmap='gray')
plt.subplot(122).set_title('output feature map', fontsize=15)
plt.imshow(outputs.squeeze().detach().numpy(), cmap='gray')
plt.savefig('conv-vis.pdf')
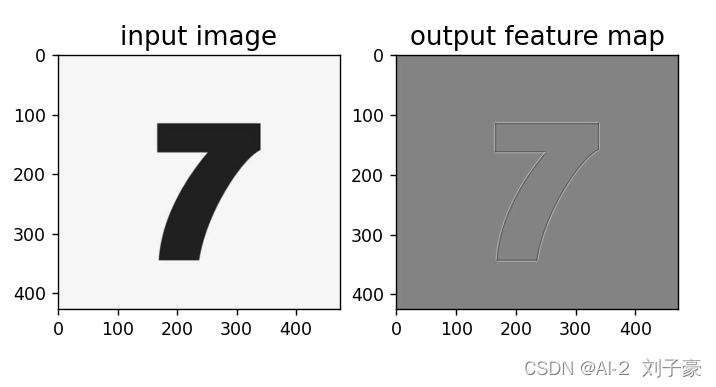
plt.show()

运行结果：

选做题

实现一些传统边缘检测算子，如：Roberts、Prewitt、Sobel、Scharr、Kirsch、Robinson、Laplacian。

代码如下：

import cv2
import numpy as np

# 加载图像
image = cv2.imread('OIP-C.jpg', 0)
image = cv2.resize(image, (800, 800))
# 自定义卷积核
# Roberts边缘算子
kernel_Roberts_x = np.array([
    [1, 0],
    [0, -1]
])
kernel_Roberts_y = np.array([
    [0, -1],
    [1, 0]
])
# Sobel边缘算子
kernel_Sobel_x = np.array([
    [-1, 0, 1],
    [-2, 0, 2],
    [-1, 0, 1]])
kernel_Sobel_y = np.array([
    [1, 2, 1],
    [0, 0, 0],
    [-1, -2, -1]])
# Prewitt边缘算子
kernel_Prewitt_x = np.array([
    [-1, 0, 1],
    [-1, 0, 1],
    [-1, 0, 1]])
kernel_Prewitt_y = np.array([
    [1, 1, 1],
    [0, 0, 0],
    [-1, -1, -1]])


# Kirsch 边缘检测算子
def kirsch(image):
    m, n = image.shape
    list = []
    kirsch = np.zeros((m, n))
    for i in range(2, m - 1):
        for j in range(2, n - 1):
            d1 = np.square(5 * image[i - 1, j - 1] + 5 * image[i - 1, j] + 5 * image[i - 1, j + 1] -
                           3 * image[i, j - 1] - 3 * image[i, j + 1] - 3 * image[i + 1, j - 1] -
                           3 * image[i + 1, j] - 3 * image[i + 1, j + 1])
            d2 = np.square((-3) * image[i - 1, j - 1] + 5 * image[i - 1, j] + 5 * image[i - 1, j + 1] -
                           3 * image[i, j - 1] + 5 * image[i, j + 1] - 3 * image[i + 1, j - 1] -
                           3 * image[i + 1, j] - 3 * image[i + 1, j + 1])
            d3 = np.square((-3) * image[i - 1, j - 1] - 3 * image[i - 1, j] + 5 * image[i - 1, j + 1] -
                           3 * image[i, j - 1] + 5 * image[i, j + 1] - 3 * image[i + 1, j - 1] -
                           3 * image[i + 1, j] + 5 * image[i + 1, j + 1])
            d4 = np.square((-3) * image[i - 1, j - 1] - 3 * image[i - 1, j] - 3 * image[i - 1, j + 1] -
                           3 * image[i, j - 1] + 5 * image[i, j + 1] - 3 * image[i + 1, j - 1] +
                           5 * image[i + 1, j] + 5 * image[i + 1, j + 1])
            d5 = np.square((-3) * image[i - 1, j - 1] - 3 * image[i - 1, j] - 3 * image[i - 1, j + 1] - 3
                           * image[i, j - 1] - 3 * image[i, j + 1] + 5 * image[i + 1, j - 1] +
                           5 * image[i + 1, j] + 5 * image[i + 1, j + 1])
            d6 = np.square((-3) * image[i - 1, j - 1] - 3 * image[i - 1, j] - 3 * image[i - 1, j + 1] +
                           5 * image[i, j - 1] - 3 * image[i, j + 1] + 5 * image[i + 1, j - 1] +
                           5 * image[i + 1, j] - 3 * image[i + 1, j + 1])
            d7 = np.square(5 * image[i - 1, j - 1] - 3 * image[i - 1, j] - 3 * image[i - 1, j + 1] +
                           5 * image[i, j - 1] - 3 * image[i, j + 1] + 5 * image[i + 1, j - 1] -
                           3 * image[i + 1, j] - 3 * image[i + 1, j + 1])
            d8 = np.square(5 * image[i - 1, j - 1] + 5 * image[i - 1, j] - 3 * image[i - 1, j + 1] +
                           5 * image[i, j - 1] - 3 * image[i, j + 1] - 3 * image[i + 1, j - 1] -
                           3 * image[i + 1, j] - 3 * image[i + 1, j + 1])

            # 第一种方法：取各个方向的最大值，效果并不好，采用另一种方法
            list = [d1, d2, d3, d4, d5, d6, d7, d8]
            kirsch[i, j] = int(np.sqrt(max(list)))
    for i in range(m):
        for j in range(n):
            if kirsch[i, j] > 127:
                kirsch[i, j] = 255
            else:
                kirsch[i, j] = 0
    return kirsch


# 拉普拉斯卷积核
kernel_Laplacian_1 = np.array([
    [0, 1, 0],
    [1, -4, 1],
    [0, 1, 0]])
kernel_Laplacian_2 = np.array([
    [1, 1, 1],
    [1, -8, 1],
    [1, 1, 1]])
# 下面两个卷积核不具有旋转不变性
kernel_Laplacian_3 = np.array([
    [2, -1, 2],
    [-1, -4, -1],
    [2, 1, 2]])
kernel_Laplacian_4 = np.array([
    [-1, 2, -1],
    [2, -4, 2],
    [-1, 2, -1]])
# 5*5 LoG卷积模板
kernel_LoG = np.array([
    [0, 0, -1, 0, 0],
    [0, -1, -2, -1, 0],
    [-1, -2, 16, -2, -1],
    [0, -1, -2, -1, 0],
    [0, 0, -1, 0, 0]])
# 卷积
output_1 = cv2.filter2D(image, -1, kernel_Prewitt_x)
output_2 = cv2.filter2D(image, -1, kernel_Sobel_x)
output_3 = cv2.filter2D(image, -1, kernel_Prewitt_x)
output_4 = cv2.filter2D(image, -1, kernel_Laplacian_1)
output_5 = kirsch(image)
# 显示锐化效果
image = cv2.resize(image, (800, 600))
output_1 = cv2.resize(output_1, (800, 600))
output_2 = cv2.resize(output_2, (800, 600))
output_3 = cv2.resize(output_3, (800, 600))
output_4 = cv2.resize(output_4, (800, 600))
output_5 = cv2.resize(output_5, (800, 600))
cv2.imshow('Original Image', image)
cv2.imshow('Prewitt Image', output_1)
cv2.imshow('Sobel Image', output_2)
cv2.imshow('Prewitt Image', output_3)
cv2.imshow('Laplacian Image', output_4)
cv2.imshow('kirsch Image', output_5)
# 停顿
if cv2.waitKey(0) & 0xFF == 27:
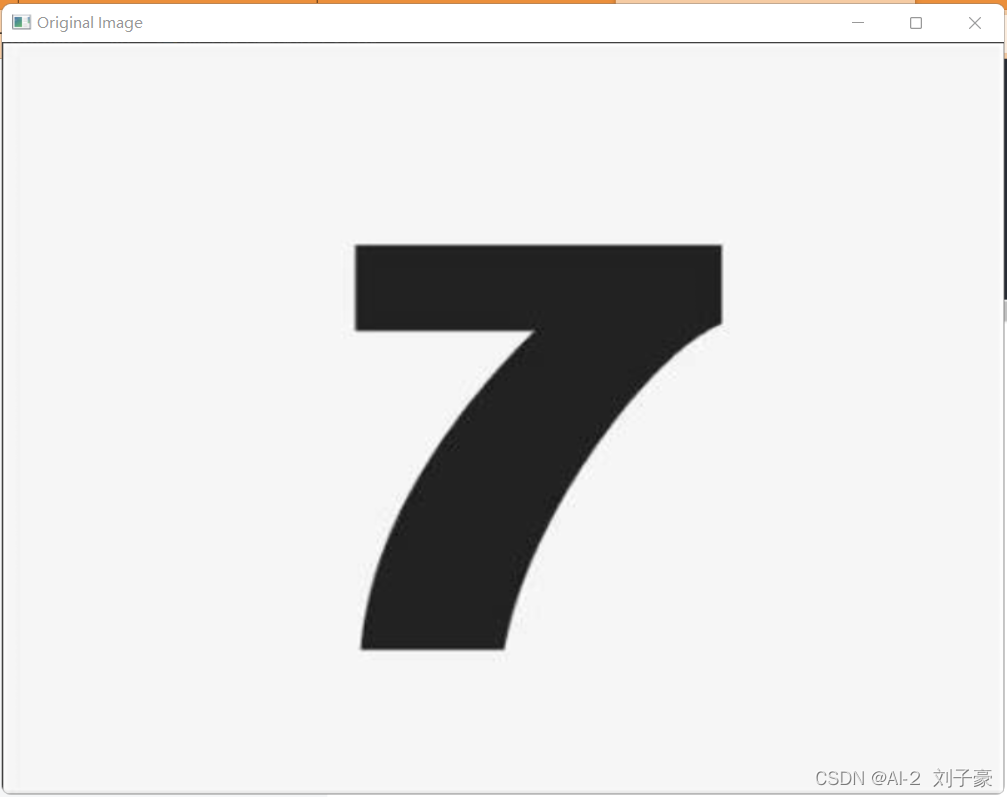
    cv2.destroyAllWindows()

运行结果：

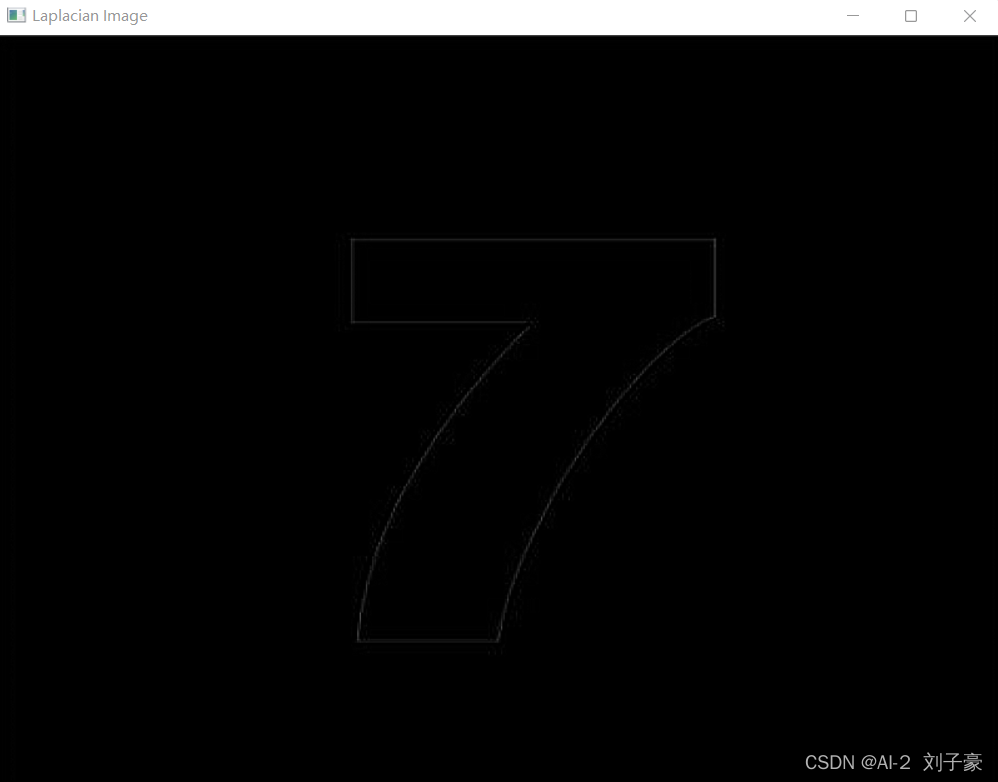
? ? ? ?从运行结果来看，kirsch边缘检测算子对本幅图检测出轮廓太复杂，Laplacian边缘检测算子对本幅图检测出轮廓太简单，Prewitt和Sobel边缘检测算子对本幅图检测结果较好。

实现的简易的?Canny?边缘检测算法

代码如下：

import cv2
# 加载图像
image = cv2.imread('OIP-C.jpg',0)
image = cv2.resize(image,(800,800))
def Canny(image,k,t1,t2):
    img = cv2.GaussianBlur(image, (k, k), 0)
    canny = cv2.Canny(img, t1, t2)
    return canny
image = cv2.resize(image, (800, 600))
cv2.imshow('Original Image', image)
output =cv2.resize(Canny(image,3,50,150),(800,600))
cv2.imshow('Canny Image', output)
# 停顿
if cv2.waitKey(0) & 0xFF == 27:
    cv2.destroyAllWindows()

运行结果：