1.论文概述

1.本论文中作者提出了一种非常深（400层）的残差通道注意力网络（RCAN），为了解决不同类别的信息在通道间被平等对待的问题以及如何构建一个更深的可训练网络问题。低分辨率的输入和特征包含丰富的低频信息，这些信息在通道间被平等对待，从而阻碍了CNNs的表征能力，而RCAN就是为了解决这一问题而被提出的。
2.本论文的创新点有两个，首先作者提出了residual in residual（RIR）结构来形成非常深的网络，RIR由几个具有长跳连接的残差组组成。每个残差组包含几个具有短跳连接的残差块。其次作者将注意力机制融入到残差块中，形成RCAB模块。

2.论文提出的背景

最近基于深度卷积神经网络（CNN）的方法相对于传统的SR方法有了显著的改进。最开始Chao Dong等人提出了一个三层的SRCNN方法。Kim等人将VDSR和DRCN将网络深度提升到了20层，比SRCNN有了明显的改进。在图像分类网络中，何凯明提出的残差学习策略被引用到了SR领域。Lim等人利用简化的残差块构建了一个非常大的EDSR网络和一个非常深的MDSR网络，并使性能得到了很大的提升，但是仅仅通过堆叠残差块来构建更深的网络很难获得更好的提升效果。更深的网络是否能够促进图像SR，以及如何构建更深的可训练网络还有待进一步的探索。
另一方面，最新的基于CNN的方法对于通道特征的处理是平等的，在处理不同类型的信息（如低频、高频信息）时缺乏灵活性。图像SR可以被看作需要尽量恢复更多高频信息的过程。LR图像包含的低频信息最多，可以直接传送到最终的HR输出，而不需要太多的计算。而领先的基于CNN的方法将从原始LR输入中提取特征，并平等地对待每个通道特征。这样的操作会在大量的低频特征上浪费不必要的计算，缺乏跨特征通道的区别性学习能力，最终阻碍了深度网络的表征能力。
为了解决上述的这些问题，作者提出了一个残差通道注意力网络（RCAN）来获得非常深的可训练网络，同时自适应地学习更多有用的通道特征。具体来说，为了使超深的网络的训练变得容易，作者提出了残差嵌套（residual in residual, RIR）结构，其中残差组（RG）作为基本模块，长跳连接（LSC）允许粗级的残差学习。在每个RG组中，通过短跳连接（SSC）将几个简化的残差块堆叠起来。通过这些基于Identity的跳跃连接，长跳连接、短跳连接以及残差中的短跳连接可以绕过大量的低频信息，从而使信息的流动更加容易。在此基础上，作者提出通道注意力机制，通过对特征通道之间的相互依赖性进行建模，来自适应地重新缩放每个通道的特征。这样的CA机制使得作者所提出的网络可以专注于更多有用的通道并增强鉴别性学习能力。

3.Residual Channel Attention Network(RCAN)

3.1 网络架构

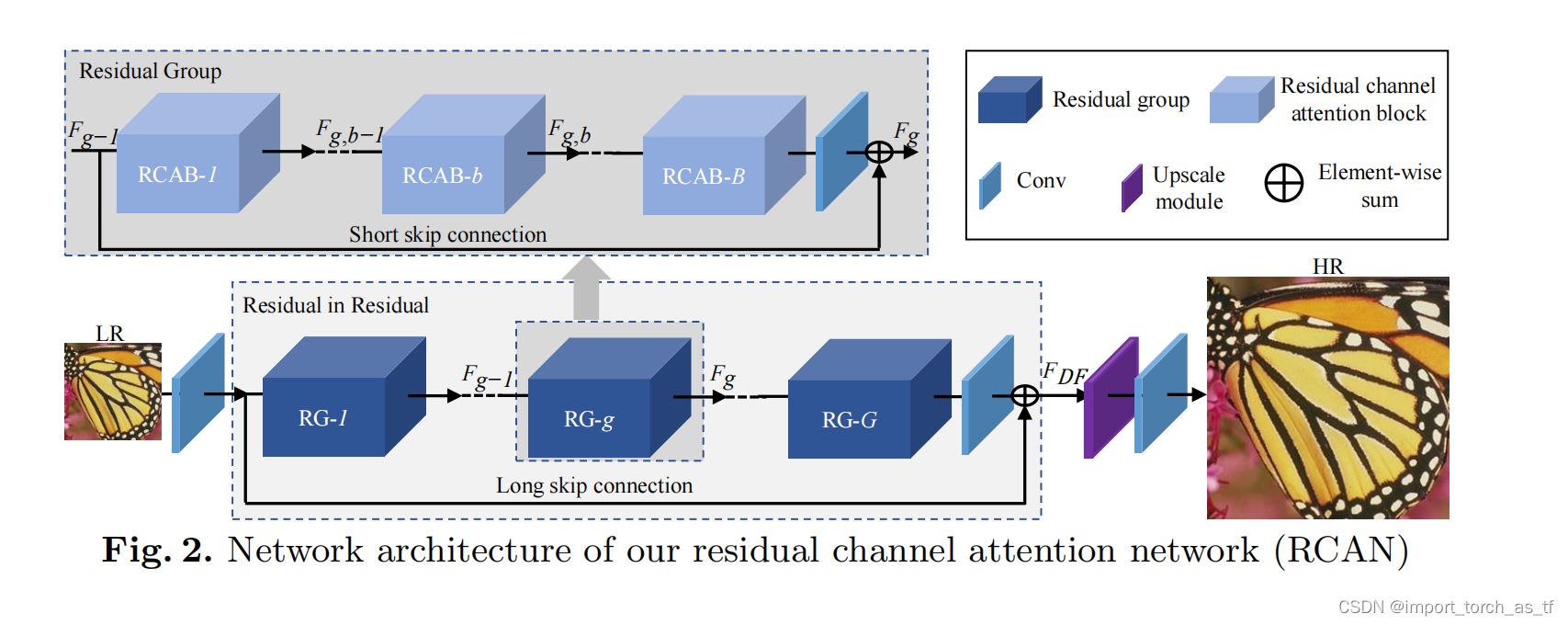
在这里插入图片描述

如图2所示。RCAN主要由四个部分组成：浅层特征提取、残差嵌套（RIR）深度特征提取、上采样模块和重建部分。
浅层特征提取：令 $I_{LR}$ 和 $I_{SR}$ 分别作为RCAN的输入和输出。作者仅使用一个卷积层从LR输入提取浅层特征 $F_0$ :
$F_{0}=H_{S F}\left(I_{L R}\right), \quad\quad\quad\quad\quad\quad\quad\quad (1)$
其中， $H_{S F}(\cdot)$ 表示卷积操作。
$F_0$ 随后用于RIR模块深层特征的提取。因此进一步可得：
$F_{D F}=H_{R I R}\left(F_{0}\right), \quad\quad\quad\quad\quad\quad\quad\quad (2)$
其中， $H_{RIR}(\cdot)$ 表示本论文提出的非常深的RIR模块，它包含G个残差组（RG）。
将RIR模块输出的深层特征 $F_{DF}$ 通过一个上采样模块进行上采样：
$F_{U P}=H_{U P}\left(F_{D F}\right), \quad\quad\quad\quad\quad\quad\quad\quad (3)$
其中， $H_{UP}(\cdot)$ 表示上采样模块。
上采样特征随后通过一个Conv层进行重建：
$I_{S R}=H_{R E C}\left(F_{U P}\right)=H_{R C A N}\left(I_{L R}\right), \quad\quad\quad\quad\quad\quad (4)$
其中， $H_{REC}(\cdot)$ 和 $H_{RCAN}(\cdot)$ 分别表示重建层和RCAN函数。
最后是损失函数的选择，本文中选择的是L1损失函数：
$L(\Theta)=\frac{1}{N} \sum_{i=1}^{N}\left\|H_{R C A N}\left(I_{L R}^{i}\right)-I_{H R}^{i}\right\|_{1}, \quad\quad\quad\quad\quad\quad (5)$
其中， $\Theta$ 表示网络的参数。损失函数通过梯度下降法进行优化。

3.2 Residual in Residual（RIR）

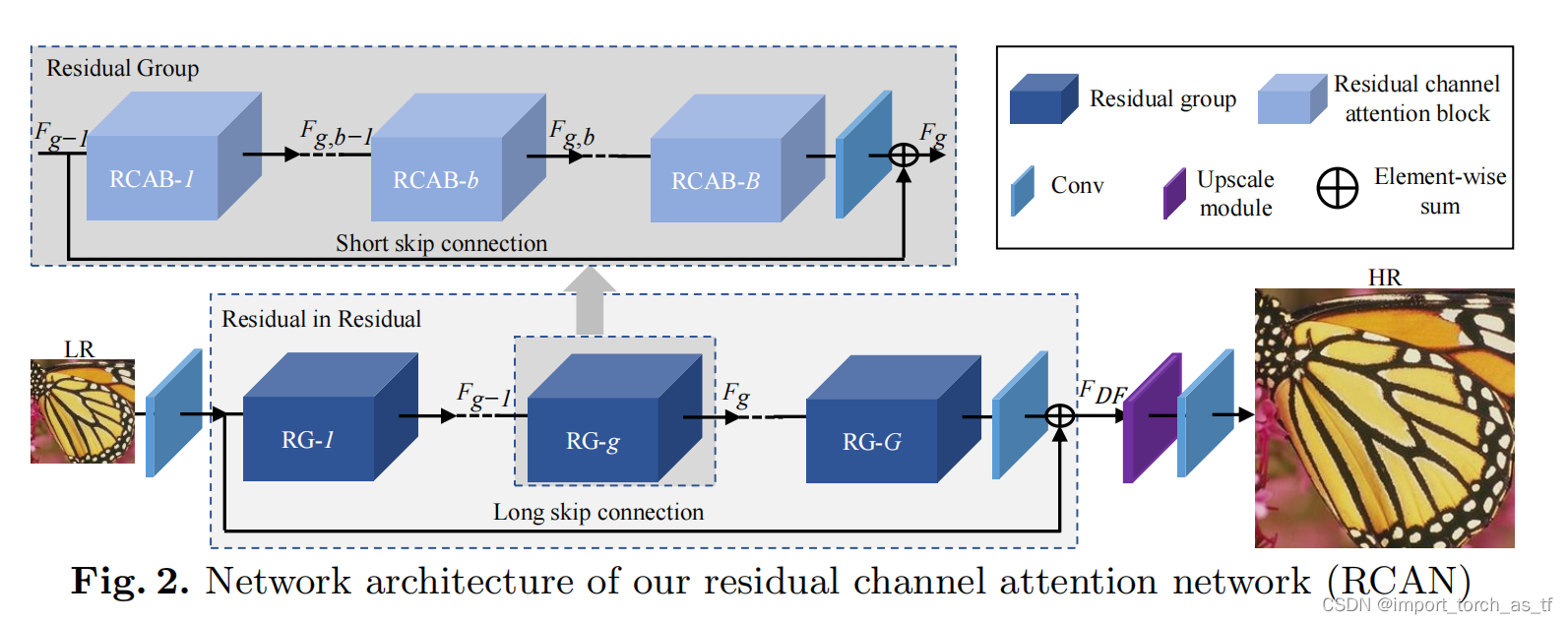
在这里插入图片描述
如图2所示，将在本下节中介绍更多关于RIR的细节。RIR模块包含G个残差组（RG）和长跳连接（LSC）。每个RG中又包含B个带有短跳连接（SSC）的残差通道注意力模块（RCAB）。作者提出的RIR模块允许训练非常深的CNN（超过400层）来获得高性能的图像SR。

研究表明，堆叠残差块和LSC可用于构造深度CNN。但是，在SR中，仅是这样简单的堆叠非常深的网络很难获得更大的性能增益，同时还会出现训练困难的问题。受到SRResNet和EDSR的启发，作者提出残差组（RG）作为更深层网络的基本模型。在第g个残差组中，RG计算为：
$F_{g}=H_{g}\left(F_{g-1}\right)=H_{g}\left(H_{g-1}\left(\cdots H_{1}\left(F_{0}\right) \cdots\right)\right), \quad\quad\quad\quad\quad\quad (6)$
其中， $H_g$ 表示第g个RG函数， $F_{g-1}$ 和 $F_g$ 是第g个RG的输入和输出。
仅堆叠许多RG将无法获得更好的性能。为了解决这个问题，RIR中进一步引入了长跳连接（LSC），以稳定非常深的网络训练。LSC还可以通过残差学习来得到更好的性能：
$F_{D F}=F_{0}+W_{L S C} F_{G}=F_{0}+W_{L S C} H_{g}\left(H_{g-1}\left(\cdots H_{1}\left(F_{0}\right) \cdots\right)\right) \quad (7)$
其中， $W_{LSC}$ 为RIR尾部Conv层的权值。为了简单起见，忽略了偏置项。LSC不仅可以简化RGs间的信息流动，而且可以使RIR在粗粒度层次上学习残差信息。LR输入和特征中包含大量丰富的信息,SR网络的目标就是恢复更多有用的信息丰富的低频信息可以通过identity的跳跃连接绕过(用长跳连接来实现)。
进一步地,作者在每个RG中堆叠B个残差通道注意力模块。在第g个RG中第b个残差通道注意力模块(RCAB)可以表示为下式:
$F_{g, b}=H_{g, b}\left(F_{g, b-1}\right)=H_{g, b}\left(H_{g, b-1}\left(\cdots H_{g, 1}\left(F_{g-1}\right) \cdots\right)\right), \quad (8)$
其中, $F_{g, b-1}$ 和 $F_{g, b}$ 是第g个RG中第b个RCAB的输入和输出,相应的函数为 $H_{g, b}$ 。
为了使主网络更加关注有价值的特征信息,在RCAB中引入短跳连接(SSC)来得到RCAB模块的输出:
$F_{g}=F_{g-1}+W_{g} F_{g, B}=F_{g-1}+W_{g} H_{g, B}\left(H_{g, B-1}\left(\cdots H_{g, 1}\left(F_{g-1}\right) \cdots\right)\right) \text {, } \quad (9)$
其中, $W_g$ 为第g个RG尾部中的Conv层的权值。SSC进一步允许网络的主要部分学习残差信息,使用LSC和SSC,在训练更容易绕过大量的低频信息(因为仅学习低频到高频之间的残差)。

1.在文中,长跳连接(LSC)是将浅层特征提取到的特征图与RIR模块输出的特征图求和,它跨越了数个RG模块。而短跳连接(SSC)是将一个RG模块的输入与输出求和,它没有跨越RG模块。
2.从整体上看,所有RG模块形成一个残差结构,而在每个RG模块内部又由数个RCAB构成了一个残差结构,因此是Residual in Residual。

3.3 Channel Attention(CA)

在以前的基于CNN的SR方法中对LR通道特征的处理是平等的,这对于实际情况来说缺乏了灵活性。为了使网络关注更加有价值的信息,作者利用特征通道间的相关性形成通道注意力机制。如图3所示。

如何为每个通道特征生成不同的注意力是关键的一步,在这里作者主要考虑了两点问题:第一,LR空间中信息具有丰富的低频成分和有价值的高频成分.低频部分似乎比较平坦.高频成分通常是充满边缘、纹理和其他细节的区域.另一方面,Conv层的每一个过滤器都有一个局部感受野.因此,卷积后的输出无法利用局部区域之外的上下文信息.
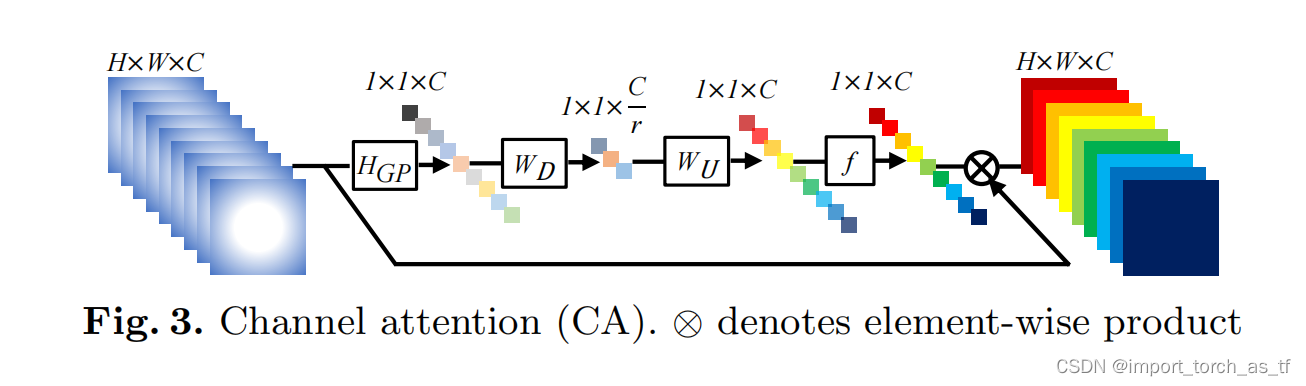
通道注意力机制操作:在上面的基础上,首先利用全局平均池化将通道相关的全局信息转化为通道描述符。如图3所示，令 $X=\left[x_{1}, \cdots, x_{c}, \cdots, x_{C}\right]$ 为输入， $X$ 表示C个大小为HxW的特征图集合。通过空间维数HxW对 $X$ 进行收缩（这里就相当进行了一个全局平均池化的操作），可以得到信道方向的统计量 $\in \mathbb{R}^{C}$ 。 $z$ 的第c个元素可以由下式计算：
$z_{c}=H_{G P}\left(x_{c}\right)=\frac{1}{H \times W} \sum_{i=1}^{H} \sum_{j=1}^{W} x_{c}(i, j) \quad\quad\quad\quad (10)$
其中， $x_{c}(i, j)$ 为第c个特征 $x_{c}$ 在 $(i, j)$ 处的值。 $H_{GP}(\cdot)$ 表示全局池化函数。这样的通道统计可以看作是局部描述符的集合，它们的统计有助于表达整个图像。
为了通过全局平均池化从聚合的信息中完全捕获通道依赖关系，作者引入了一种门控机制。在本文中，作者选择sigmoid函数作为门控机制：
$s=f\left(W_{U} \delta\left(W_{D} z\right)\right) \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad (11)$
其中， $f(\cdot)$ 和 $\delta(\cdot)$ 分别表示sigmoid函数和ReLU函数。 $W_D$ 为卷积层的权值，卷积运算以缩减比 $r$ 进行通道缩减。在由ReLU激活后，低维信号随后通过权值为 $W_U$ 的通道上采样层以比率 $r$ 增加，恢复到与原来相同的高维信号。然后我们获得最终的特征统计量 $s$ ，用于重新缩放输入 $x_c$ ：
$\widehat{x}_{c}=s_{c} \cdot x_{c} \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad (12)$
其中， $s_c$ 和 $x_c$ 为第c个通道的缩放因子和特征图。在通道注意力机制下，对RCAB中的残差分量进行自适应缩放。

3.4 Residual Channel Attention Block(RCAB)

残差组（RG）和长跳连接（LSC）允许网络的主要部分关注LR特征中更有信息的成分。通道注意力机制提取通道间的通道统计量，进一步提高网络的鉴别性能力。同时受到EDSR中残差模块（RB）成功的启发，作者将CA融合到RB中，提出了残差通道注意块（RCAB），如下图4所示：
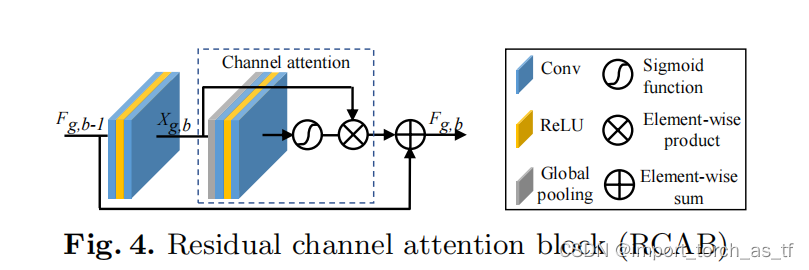
对于第g个RG中的第b个RCAB（原文中说的是RB，我觉得应该就是RCAB），由下式定义：
$F_{g, b}=F_{g, b-1}+R_{g, b}\left(X_{g, b}\right) \cdot X_{g, b} \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad (13)$
其中， $R_{g,b}$ 表示特征注意函数。 $F_{g,b}$ 和 $F_{g,b-1}$ 为RCAB的输入和输出，RCAB从输入中学习残差 $X_{g,b}$ 。残差成分主要由两个堆叠的卷积获得：
$X_{g, b}=W_{g, b}^{2} \delta\left(W_{g, b}^{1} F_{g, b-1}\right) \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad (14)$
其中， $W^1_{g,b}$ 和 $W^2_{g,b}$ 为RCAB中的两个堆叠Conv层的权重集合。
作者在论文中进一步将RCAB模块与EDSR/MDSR模型中的RB模块进行比较。RB模块可以看作是RCAB模块的一种特例。MDSR中的RB模块没有残差缩放层，与将 $R_{g,b}( \cdot)$ 令为常数1时的RCAB模块相同。假定EDSR中的RB模块中的残差缩放层rescaling设为0.1，这与将 $R_{g,b}( \cdot)$ 令为常数0.1时的RCAB模块相同。在残差中引入残差缩放层是为了训练非常宽的网络，但是EDSR中没有考虑通道之间的相互依赖性。

3.5实现细节

在RIR结构中将RG的个数设为G=10。在每个RG中，作者将RCAB个数设置为20。所有卷积层的尺寸设为3x3，除了通道下采样和通道上采样，它们中的卷积核尺寸为1x1。对于卷积核大小为3x3的卷积层，采用补零操作保持特征图尺寸大小不变。在浅层特征提取和RIR结构中，Conv层有C=64个滤波器。通道下采样中卷积层有 $\frac{C}{r}=4$ 个滤波器，其中缩减比 $r$ 设为16。对于上采样模块 $H_{up}( \cdot)$ ，使用ESPCNN将粗分辨率特征提升到细分辨率特征，这与RDN相同（RDN和RCAN是同一个作者）。

4.实验

4.1设置

数据集和退化模型：采用DIV2K数据集的800图像进行训练。采用5个基准数据集进行测试：Set5、Set14、B100、Urban100和Manga109。采用双三次线性插值（BI）和模糊降级（BD）作为退化模型。
评估指标：采用PSNR和SSIM在转换后的YCbCr色彩空间的Y通道上评估SR结构。
训练设置：以90°、180°和270°随机旋转和水平翻转进行数据增强。在每个batch中，提取16个大小为48x48的patchLR作为输入。使用L1损失函数和Adam优化器， $\beta_{1}$ 和 $\beta_{2}$ 分别默认取0.9和0.999。初始学习率为1x $10^{-4}$ ，每2x $10^{5}$ 次反向传播减少一半。

4.2 RIR和CA的有效性

RIR：为了证明RIR结构的有效性，作者从很深的网络中移除长跳连接（LSC）和短跳连接（SSC）。在实现的细节中已经描述过，RG=10，每个RG中有20个RCAB模块，每个模块中包含两个Conv层，因此RCAN超过400个Conv层的非常深的网络。在表一中，当LSC和SSC同时被移除时，无论是否使用通道注意力机制（CA），在数据集Set5（x2）上的PSNR值都将对较低。
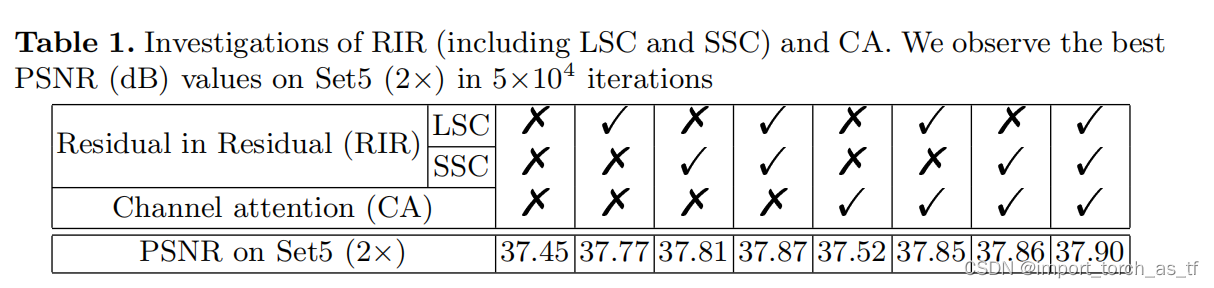
在这里插入图片描述
从上述的比较结构表明，LSC和SSC对于非常深的网络是必不可少的。
CA：当对表一的前四列和后四列进行比较，可以发现有CA的网络比没有CA的网络表现得更好。非常深的网络可以达到非常高的性能，但是很深的网络很难得到进一步的改善，但是通过CA可以使深层网络的性能得到进一步改善。即使在没有RIR的情况下（也就是简单的堆叠残差结构），CA也可以将性能从37.45dB提高到37.52dB。这些比较表明了对通道特征的自适应关注确实提高了性能。

4.3 在BI退化模型上的实验结果

作者将RCAN与11种最先进的方法进行了比较：SRCNN、FARCNN、SCN、VDSR、LapSRN、MemNet、EDSR、SRMDNF、D-DBPN、RDN（是的论文就给了10个）。同时作者也引入了自集成策略来进一步提升RCAN的性能，并称该模型为RCAN+。

定量性结果：表2显示了在x2、x3、x4和x8比例下SR的定量比较。RCAN+在所有比例下的所有数据集上执行得最好。即使没有自集成，RCAN也优于其他的方法。
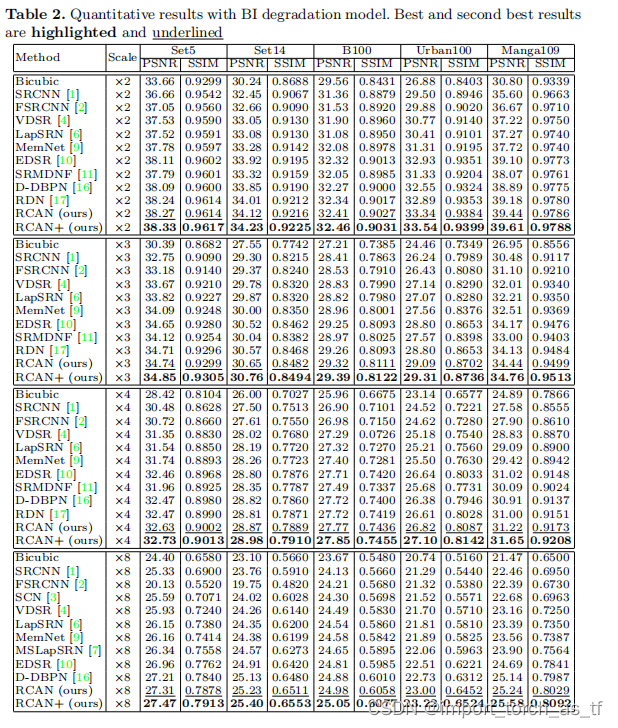
在这里插入图片描述
可视化结果：在图5中，展示了在比例x4的可视化比较。对于最上面的图像，大多数的方法无法恢复里面的小圆格，并且会产生模糊的伪影。相比之下，RCAN可以更好的缓解模糊的伪影，并恢复更多的细节。对于中间图像，大多数的方法沿水平线的模糊伪影。在许多方法中很多线条完全都是混乱的，只有RCAN产生更接近ground truth。对于最下面的图像，裁剪部分可以看到充满了纹理。所有其他的方法都产生了严重的模糊伪影，只有RCAN能够明显地恢复它们，更接近ground truth。
之后的结构不在总结，有点过于浪费时间，想知道结果的同学可以详细看论文
在这里插入图片描述
当比例因子变大后（x8），双三次插值的结果会丢失很多结构，这种错误的缩放结果也会导致一些最先进的方法产生完全错误的结构。而RCAN能够恢复它们。