1、概念
谱聚类是从图论中演化出来的算法，它将聚类问题转换成一个无向加权图的多路划分问题。主要思想是把所有数据点看做是一个无向加权图 G = ( V，E ) 的顶点 V ，E 表示两点间的权重，数据点之间的相似度越高权重值越大。然后根据划分准则对所有数据点组成的图进行切图，使切图后不同的子图间的边权重和尽可能低，而子图内的边权重和尽可能高，从而实现聚类的效果。
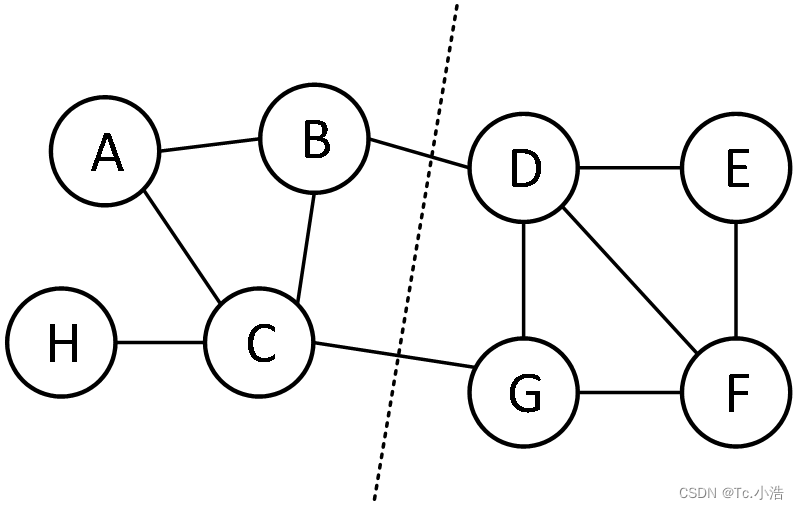
简单来说，谱聚类一般有两个步骤：1. 图表示，将数据表示为图的形式，最常见的就是拉普拉斯矩阵；2. 图划分，根据划分准则对图进行切割，形成聚类。
2、相似性度量
似性度量是用来衡量数据之间的相似程度。在谱聚类中，无向图的权重就是用数据间的相似性来表示的。相似性度量的方法种类很多，一般需要根据实际情况进行选用。常用的度量方法有欧式距离、高斯核函数、余弦相似度等。
- 欧式距离
欧氏距离是一种最为常用的度量方法，其定义如下：
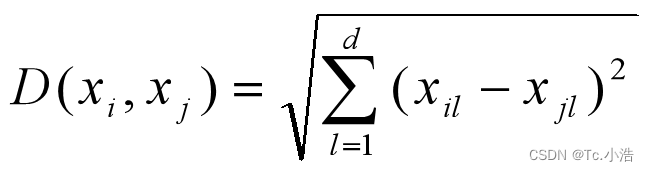
其中xi与xj两个数据点。数据点之间的距离越小，相似度越高。在特征空间中，欧式距离具有转化和旋转的不变性，因此更倾向于构建球形的聚类簇。 - 高斯核函数
谱聚类中常使用高斯核函数来定义边的权重，其计算公式为：
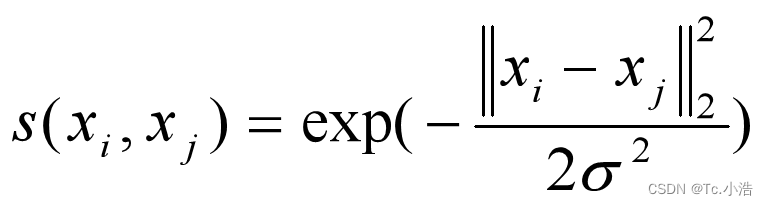
其中 xi 与 xj 表示一个 d 维的数据点向量，σ 为函数的宽度参数。参数 σ 的值越大，数据点之间的相似性越高，需要根据实际情况调整。从式中可以看出，如果数据点之间的欧氏距离远高于参数 σ 的值，高斯核函数的值就会趋于零，因此只有与 σ 值相当的数据点间的距离才会起作用。 - 余弦相似度
余弦相似度常使用在文本聚类中，其表示形式为：
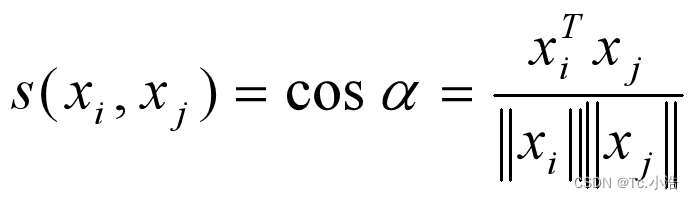
在文本聚类中，传统的欧式距离往往不能很好地描述文本对象之间的相似性，此时就需要非距离测量的相似性度量。对于余弦相似度来说，越是相似的样本，在特征空间里越趋于平行，其余弦值也越大。
3、相似矩阵（权重矩阵）、度矩阵、拉普拉斯矩阵
给定包含了 n 个数据点的集合，可以构建一个无向加权图 G = ( V，E ) ，其中 V 表示数据集里所有的点 (v1, v2, … , vn) ，对于 V 中任意两个点 ，都可以有边连接。确定相似性度量方法后，就可以得到各个边的权重，定义权重 wij 为点 vi 和点 vj 之间的边权重，即可得到相似矩阵 W。由于该图是无向图，所以 wij =wji 且 wij ≥ 0。
- 相似矩阵(权重矩阵)
对于一幅无向图??G=(V,E)，学过图论或者数据结构的同学都知道，他有两个很重要的概念是图的邻接矩阵和顶点的度。所有顶点之间的权重构成一个nxn???矩阵，叫做邻接矩阵，也叫权重矩阵，即：
对于无向图，顶点vi??与顶点vj??之间的权重和顶点vj??与顶点?vi?之间的权重是一样的，因而??wij=wji，因此w??是对称矩阵，即w=w^T???。这个邻接矩阵稍后将作为图的相似矩阵。注意这里的相似矩阵不是矩阵的相似。 - 度与度矩阵
对于图中的任意一点vi，它的度di定义为与它相连所有边的权重之和（跟数据结构不同，不是链接顶点的个数）：
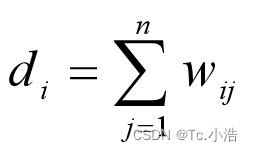
顶点vi的度其实就是邻接矩阵第i行的和(第i列的和也可以，因为?是对称矩阵)。
- 拉普拉斯矩阵
通过该定义，我们就可以得到一个 n × n 的度矩阵 D = diag( d1, d2, …, dn )。通过相似矩阵 W 和度矩阵 D，就可以计算出拉普拉斯矩阵 L = D - W，它有一些很好的性质：
（1）由W和D都是对称矩阵，可以推出拉普拉斯矩阵是对称矩阵；
（2）由于拉普拉斯矩阵是对称矩阵，所以它的特征值都是实数；
（3）对于任意的向量f，可以推导出：
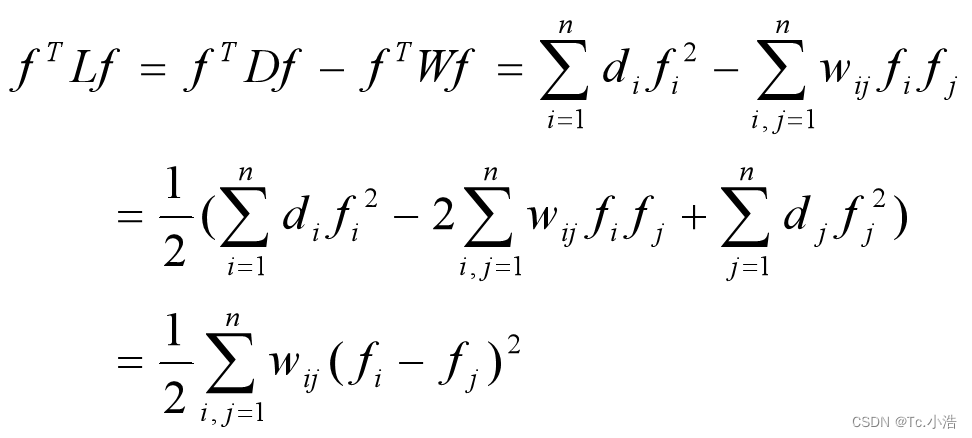
（4）由性质（3）可知，拉普拉斯矩阵是半正定，对应n个实数特征值都大于或等于0；
4、图的划分准则
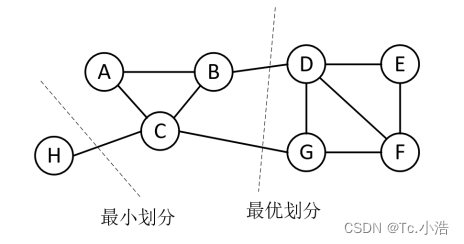
聚类算法将聚类问题转化成图的划分问题，最优划分原则是切图后不同的子图间边权重和最小，而子图内的边权重和最大，要找到满足这个优化问题的解是一个NP-难的问题，因此需要使用维数归约的思想去近似地解决这个问题。聚类结果的好坏会直接受划分准则的影响，常见的划分准则有最小割集准则 (Minimum cut，Mcut)、比例割集准则 (Ratio cut，Rcut)、规范割集准则 (Normalized cut，Ncut) 等。
要将无向图 G 划分成 k 个相互无连接的子图，每个子图点集合为 A1, A2, … , Ak ，它们满足 Ai ∩ Aj = Φ 且 A1∪A2∪…∪Ak = V。对于任意两个子图点的集合 A, B ∈ V，A ∩ B = Φ，定义 A 和 B 子图之间的权重为：
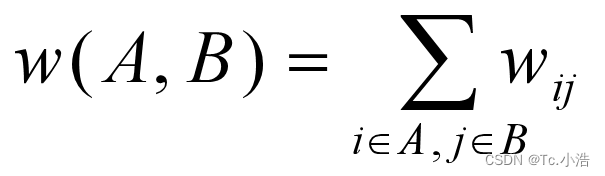
- 最小割集准则希望使子图之间的边权重之和最小，其代价函数为：
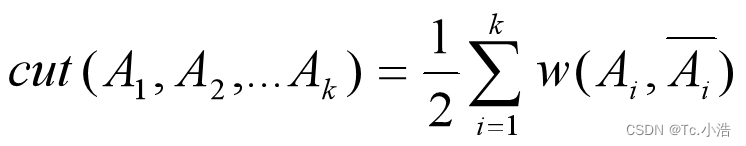
其中 ￣Ai 为 Ai 的补集。通过最小化上述代价函数来实现图的分割，在一些图像分割上取得了不错的效果，但该准则很容易出现倾斜分割的现象，因此又提出了规范割集准则和比例割集准则来限制每个子图的规模。
- 比例割集准则不仅考虑最小化子图间的权重和，还考虑最大化每个子图中点的个数，其目标函数为：
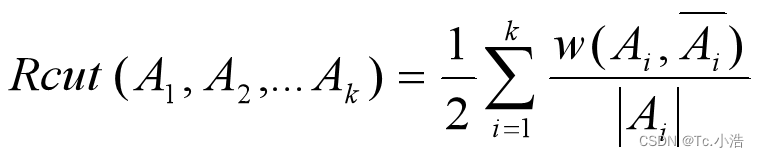
其中 |Ai| 表示子集 Ai 中点的个数。Rcut 避免了倾斜分割的问题，但运行效率不高。 - 规范割集准则与比例割集准则相似，该准则考虑的是最大化每个子图中的权重和，目标函数为：
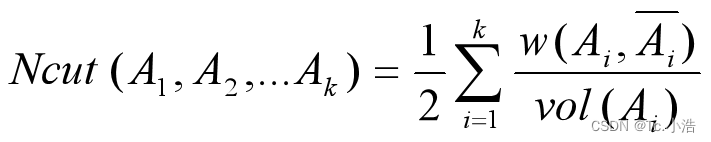
其中 vol( Ai ) 表示子集 Ai 中的权重和。
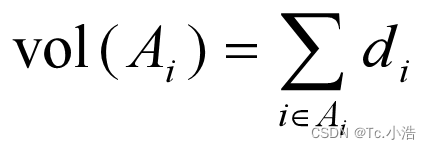
5、Ncut聚类
在谱聚类中，最常用的相似性度量是高斯核函数，最常用的划分准则是 Ncut。下面主要介绍如何最小化 Ncut 目标函数得到聚类结果。引入一个指示矩阵 H ∈ Rn×k，其中包含 k 个 n 维指示向量 hj ∈ { h1, h2, … ,hk }，定义 hij 为：
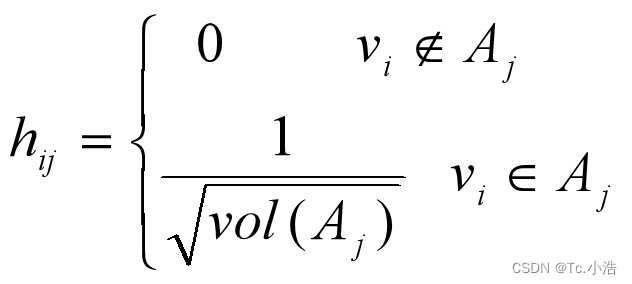
可以推导出：
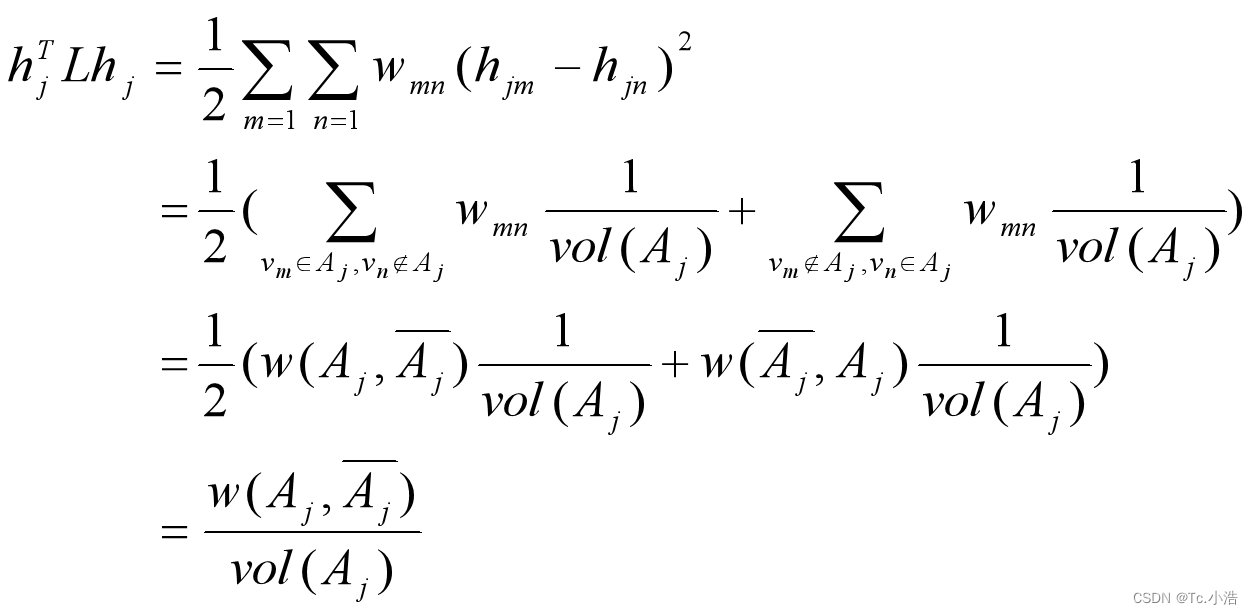
其中L为拉普拉斯矩阵。优化目标为：
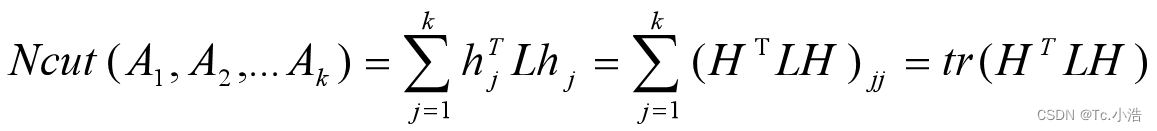
且
H
T
D
H
H^TDH
HTDH = I，D 为度矩阵。因此，优化目标为：
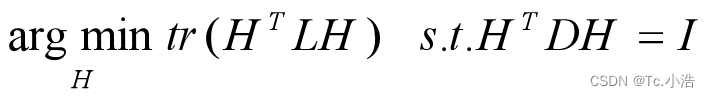令
H
=
D
?
1
/
2
F
H = D^{-1/2}F
H=D?1/2F，则：
H
T
L
H
=
F
T
D
?
1
/
2
L
D
?
1
/
2
F
，
H
T
D
H
=
F
T
F
=
I
H^TLH = F^TD^{-1/2}LD^{-1/2}F，H^TDH = F^TF = I
HTLH=FTD?1/2LD?1/2F，HTDH=FTF=I，也就是说优化目标变成了：
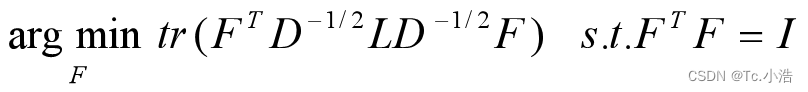
D
?
1
/
2
L
D
?
1
/
2
D^{-1/2}LD^{-1/2}
D?1/2LD?1/2 相当于对拉普拉斯矩阵 L 进行标准化。可以观察到
t
r
(
F
T
D
?
1
/
2
L
D
?
1
/
2
F
)
tr( F^TD^{-1/2}LD^{-1/2}F )
tr(FTD?1/2LD?1/2F) 中每一个优化子目标
f
i
T
D
?
1
/
2
L
D
?
1
/
2
f
i
f_i^TD^{-1/2}LD^{-1/2}f_i
fiT?D?1/2LD?1/2fi? ，
其中
f
i
是单位正交基，
D
?
1
/
2
L
D
?
1
/
2
是对称矩阵，此时
f
i
T
D
?
1
/
2
L
D
?
1
/
2
f
i
的最小值就是
D
?
1
/
2
L
D
?
1
/
2
的最小特征值，因此，只需要找到最小的前
k
个特征值以及其对应的特征向量，标准化后就可以得到最后的特征矩阵
F
，从而近似地解决这个
N
P
难的问题。由于在该过程中损失了少量信息，得到的矩阵
F
不能完全指示各样本归属，因此需要再使用一次
k
?
m
e
a
n
s
算法或其他离散化过程。
其中 f_i 是单位正交基，D^{-1/2}LD^{-1/2} 是对称矩阵，此时 f_i^TD^{-1/2}LD^{-1/2}f_i 的最小值就是 D^{-1/2}LD^{-1/2} 的最小特征值，因此，只需要找到最小的前 k 个特征值以及其对应的特征向量，标准化后就可以得到最后的特征矩阵 F，从而近似地解决这个NP难的问题。由于在该过程中损失了少量信息，得到的矩阵 F 不能完全指示各样本归属，因此需要再使用一次 k-means 算法或其他离散化过程。
其中fi?是单位正交基，D?1/2LD?1/2是对称矩阵，此时fiT?D?1/2LD?1/2fi?的最小值就是D?1/2LD?1/2的最小特征值，因此，只需要找到最小的前k个特征值以及其对应的特征向量，标准化后就可以得到最后的特征矩阵F，从而近似地解决这个NP难的问题。由于在该过程中损失了少量信息，得到的矩阵F不能完全指示各样本归属，因此需要再使用一次k?means算法或其他离散化过程。
下面总结 Ncut 聚类流程：
输入：数据集 X = { x1, x2, … , xn }，聚类个数 k
输出：簇划分
1. 根据数据集构造相似矩阵 W，度矩阵 D ；
2. 计算拉普拉斯矩阵 L，并标准化 D-1/2LD-1/2 ；
3. 计算 D-1/2LD-1/2 最小的 k 个特征值对应的特征向量 f ；
4. 将各个特征向量 f 组成的矩阵按行标准化，组成特征矩阵 F ∈ Rn×k；
5. 将 F 中的每一行作为一个 k 维的数据点，使用 k-means 或其他离散化过程获取聚类指标。
可以看出，PCA 优化过程与谱聚类非常相似，只不过谱聚类是找前 k 个最小的特征值对应的特征向量。