本文章包含以下内容:
????????数据: lris数据集;
????????模型: 前馈神经网络;
? ? ? ? 激活函数: Logistic
????????损失函数: 交叉嫡损失;
????????优化器: 梯度下降法;
????????评价指标 :准确率。
输出层使用了Softmax分类
通过使用前馈神经网络实现BP学习算法,进一步理解前馈神经网络的分类任务。
?
1.实验数据集
????????Iris(1).csv无法上传,这里就不提供下载了,它长这样
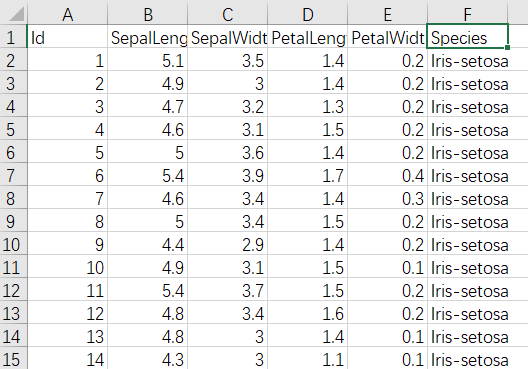
????????lris数据集,也称为鸢尾花数据集,包含了3种鸢尾花类别(Setosa · Versicolour - Virginica),每种类别有50个样本,共计150个样本。其中每个样本中包含了4个属性:花尊长度﹑花芎宽度﹑花瓣长度以及花瓣宽度,本实验通过鸢尾花这4个属性来判断该样本的类别。
2.读取数据集
????????实验中将数据集划分为两部分:训练集:用于确定模型参数;测试集:用于估计应用效果。
在本实验中,将2/3数据用于模型训练, 1/3数据用于模型测试。
3.模型构建
????????使用前馈神经网络模型进行鸢尾花分类实验,将模型的输入神经元个数定义为4,隐藏层神经元个数定义为6,输出神经元个数定义为3。
4.模型训练与预测
????????使用训练集进行模型训练,使用测试数据对模型进行预测,观察模型在测试集上的准确率情况。
代码如下:
import numpy as np
import pandas as pd
import torch
# 读取数据
def read_data(file):
# 读取csv文件,并存入data,带标签 dataframe
data = pd.read_csv(file)
data = data.sample(frac=1).reset_index(drop=True) # 打乱数据集
y = list(data['Species']) # 标签
len_data = len(y) # 数据个数
# labels 删除的列标签,axis=1 删除列,inplace=True 改变原数据
data.drop(labels=['Id', 'Species'], axis=1, inplace=True) # 删除Id,Species列
# Species 转独热向量
for i in range(len(y)):
if y[i] == 'Iris-setosa':
y[i] = [1, 0, 0]
elif y[i] == 'Iris-versicolor':
y[i] = [0, 1, 0]
elif y[i] == 'Iris-virginica':
y[i] = [0, 0, 1]
y = torch.Tensor(y) # 转张量
data = torch.Tensor(data.values) # 转张量
# train 训练
# test 测试
return [[data[0:int(len_data * 0.8)], y[0:int(len_data * 0.8)]],
[data[int(len_data * 0.8):len_data], y[int(len_data * 0.8):len_data]]]
# 初始化参数 通过从均值为0﹑标准差为0.01的正态分布中采样随机数来初始化权重
# 并将偏置初始化为0。
def chushi():
# 返回从正态分布中提取的随机数的张量,该正态分布的均值是mean,标准差是std。
# requires_grad=True 表示需要计算梯度
w1 = torch.normal(mean=0.01, std=0.01, size=(4, 6), requires_grad=True)
w2 = torch.normal(mean=0.01, std=0.01, size=(6, 3), requires_grad=True)
# 返回6个类型为torch.dtype,值为 0 的tensor
b = torch.zeros(6, requires_grad=True)
return w1, w2, b
# 测试函数,比较准确率
def ceshi(w1, w2, b, f, l):
c = 0
# 模型计算出所有的结果
l1 = Model(f, w1, w2, b)
for i in range(len(l)):
# 如果最大值对应的l值是1,说明验证正确。
s = -1
t = float('-inf')
for j in range(len(l[0])):
if l1[i][j] > t:
t = l1[i][j]
s = j
if l[i][s]:
c = c + 1
return c / len(l)
# 该函数接收批量大小﹑特征矩阵和标签向量作为输入,生成大小为batch_size的小批量,每个小批量包含一组特征和标签。
def data_iter(batch_size, features, labels): # 批量 特征 标签
for i in range(len(labels) - batch_size):
test_index = np.random.choice(len(features), batch_size, replace=False)
yield features[test_index], labels[test_index]
def softexp(A):
A = A.exp()
A_sum = A.sum(axis=1, keepdims=True)
A = A / A_sum
return A
# 输出层为 softmax 输入特征为x﹑权重为w
def softmax(X, w):
S = torch.matmul(X, w)
return softexp(S)
# 激活函数计算神经元的净活性值 (输出)
def Activation(z):
# Logistic
return 1 / (1 + torch.exp(-z))
# 激活函数导数
def Activation_(z):
return torch.exp(-z)*(Activation(z)**2)
# 计算神经元的活性值 (输入) 输入特征为x﹑权重为w
def Calculation(z_old, w, b):
return torch.matmul(z_old, w) + b
# 模型,计算网络输出
def Model(x, w1, w2, b):
y_hat = softmax(Activation(Calculation(x, w1, b)), w2)
return y_hat
# 交叉熵损失函数,返回损失值,其中y_hat为预测值, y为真实值。
def cross_entropy_loss(y_hat, y):
lo = -(torch.log(y_hat) * y)
return lo / len(y)
# 从数据集中随机抽取小批量样本,根据参数计算损失的梯度;然后朝着减少损失的方向更新参数。
# 实现小批量随机梯度下降更新,该函数接受模型参数集合﹑学习速率和批量大小作为输入。
def sgd(params, lr, batch_size):
# wi_new = wi - lr * g(wi)
for param in params:
param.data = param - lr * param.grad / batch_size
param.grad.zero_() # 梯度清零
def xunlian(batch_size, features, labels, w1, w2, b):
lr = 0.03 # 学习率
num_epochs = 83 # 循环次数
net = Model # 模型
loss = cross_entropy_loss # 损失函数
for epoch in range(num_epochs):
for X, y in data_iter(batch_size, features, labels):
# l = loss(Model(X, w1, w2, b), y)
# l.sum().backward()
# sgd([w1, w2, b], lr, batch_size)
z = Calculation(X, w1, b) # 隐藏层输入
a = Activation(z) # 隐藏层输出
a_y = softmax(a, w2) # 输出层输出
S_2 = (a_y - y)
S_1 = Activation_(z) * torch.matmul(S_2, w2.T) # 第l层误差项 δ(l) = f'(z(l)).*(w(l+1).T*δ(l+1))
w1.data = w1 - lr * torch.matmul(X.T, S_1) # w的梯度为: δ(l)a(l-1).T
b.data = b - lr * S_1.sum(0) # b->6 S_1->6 S_2->3
w2.data = w2 - lr * torch.matmul(a.T, S_2) # 更新w2
if epoch % 10 == 0: # 每循环10次执行
with torch.no_grad(): # 输出当前误差,循环次数
train_l = loss(net(features, w1, w2, b), labels)
print(f'epoch {epoch}, loss {float(train_l.mean()):f}')
c = ceshi(w1, w2, b, features, labels, ) # 看一看在训练集上的准确率
print('训练集准确率:', c * 100, "%")
file = 'Iris(1).csv' # 数据文件
[[X_train, y_train],
[X_test, y_test, ]] = read_data(file) # 读取数据集
w1, w2, b = chushi() # 初始化 w,b
batch_size = 8 # 批量大小为 8
# 训练函数
xunlian(batch_size, X_train, y_train, w1, w2, b)
print('训练完成====================================')
c = ceshi(w1, w2, b, X_test, y_test) # 测试集准确率
print('测试集准确率:', c * 100, "%")
print('所得参数如下:\n', w1, '\n', w2, '\n', b, '\n')
print('例子:\n X值:', X_test[0:1])
print('实际y', y_test[0:1])
print('预测y', Model(X_test[0:1], w1, w2, b))
# print(w)
结果示例:
epoch 0, loss 0.001769
训练集准确率: 89.16666666666667 %
epoch 10, loss 0.000364
训练集准确率: 95.0 %
epoch 20, loss 0.000290
训练集准确率: 95.83333333333334 %
epoch 30, loss 0.000243
训练集准确率: 96.66666666666667 %
epoch 40, loss 0.000414
训练集准确率: 93.33333333333333 %
epoch 50, loss 0.000163
训练集准确率: 99.16666666666667 %
epoch 60, loss 0.000198
训练集准确率: 96.66666666666667 %
epoch 70, loss 0.000196
训练集准确率: 97.5 %
epoch 80, loss 0.000161
训练集准确率: 98.33333333333333 %
训练完成====================================
测试集准确率: 96.66666666666667 %
所得参数如下:
tensor([[ 0.9806, 3.0590, -0.8039, -0.5332, 3.0937, -1.1383],
[ 1.3435, 3.1047, -1.8155, -1.8243, 3.6250, -2.1197],
[-1.9728, -5.2749, 2.0337, 3.0097, -5.6045, 2.5650],
[-2.3027, -4.6498, 2.3441, 1.5330, -4.8966, 2.7566]],
requires_grad=True)
tensor([[ 2.9231, 0.0412, -2.9310],
[ 2.7915, 1.0842, -3.8255],
[-2.7528, -0.1600, 2.9669],
[-5.7803, 4.2794, 1.5421],
[ 3.0054, 1.1464, -4.1305],
[-2.7934, -0.3414, 3.1587]], requires_grad=True)
tensor([ 1.5407, 3.5230, -1.5978, -0.3448, 3.7239, -1.9607],
requires_grad=True)
例子:
X值: tensor([[5.8000, 2.7000, 4.1000, 1.0000]])
实际y tensor([[0., 1., 0.]])
预测y tensor([[1.6022e-03, 9.9839e-01, 4.5279e-06]], grad_fn=<DivBackward0>)
进程已结束,退出代码为 0
epoch 0, loss 0.001729
训练集准确率: 69.16666666666667 %
epoch 10, loss 0.000181
训练集准确率: 98.33333333333333 %
epoch 20, loss 0.000888
训练集准确率: 84.16666666666667 %
epoch 30, loss 0.000198
训练集准确率: 96.66666666666667 %
epoch 40, loss 0.000119
训练集准确率: 98.33333333333333 %
epoch 50, loss 0.000122
训练集准确率: 98.33333333333333 %
epoch 60, loss 0.000104
训练集准确率: 98.33333333333333 %
epoch 70, loss 0.000119
训练集准确率: 98.33333333333333 %
epoch 80, loss 0.000130
训练集准确率: 98.33333333333333 %
训练完成====================================
测试集准确率: 96.66666666666667 %
所得参数如下:
tensor([[ 2.6183, -0.4223, 3.1955, 3.5719, -0.5553, -0.0769],
[ 1.8743, -1.8185, 1.9431, 3.4956, -2.2456, -2.2022],
[-3.6397, 2.7688, -4.2452, -4.6510, 1.8316, 1.3680],
[-4.6315, 1.4771, -5.4197, -6.4368, 2.3386, 1.7676]],
requires_grad=True)
tensor([[ 2.7592, 0.5953, -3.3437],
[-5.3697, 3.2962, 2.1221],
[ 2.7891, 0.7843, -3.5567],
[ 2.9859, 0.7118, -3.6540],
[-3.0911, -0.2803, 3.4012],
[-3.8995, 0.2174, 3.7301]], requires_grad=True)
tensor([ 2.2708, -0.2802, 2.6552, 3.3875, -1.1425, -0.7772],
requires_grad=True)
例子:
X值: tensor([[6.4000, 3.1000, 5.5000, 1.8000]])
实际y tensor([[0., 0., 1.]])
预测y tensor([[3.3414e-08, 3.7522e-02, 9.6248e-01]], grad_fn=<DivBackward0>)
进程已结束,退出代码为 0