由于课时压缩,两个实验一起提交,故把这两个实验合并成一篇博客。因为这两部分的知识点之前我正好都写过博客(KMeans,PCA;但是当时的代码写得不太简练,这篇博客里会重置一遍),所以这篇博客会没有前两篇实验详细,还请谅解。
实验三:KMeans
这个实验原来还包含GMM的部分,但是压缩后只做KMeans的部分就可以了。简单介绍一下KMeans:KMeans是一种常用的聚类算法,在给定聚类数
k
k
k后,它的目标是最小化平方误差
E
=
∑
i
=
1
k
∑
x
∈
C
i
∣
∣
x
?
μ
i
∣
∣
2
2
E=\sum\limits_{i=1}^k\sum\limits_{x\in C_i}||\pmb x-\pmb\mu_i||_2^2
E=i=1∑k?x∈Ci?∑?∣∣xx?μμi?∣∣22?
其中
μ
i
=
1
∣
C
i
∣
∑
x
∈
C
i
x
\pmb\mu_i=\frac{1}{|C_i|}\sum_{x \in C_i}\pmb x
μμi?=∣Ci?∣1?∑x∈Ci??xx是簇(cluster)
C
i
C_i
Ci?的均值向量。这一式子的文字描述即“每个样本点到它所述属的距离之和”。这个式子无法求得解析解,KMeans采用迭代的方式来逼近最优解(因此也就可能陷入局部最优)。KMeans的算法描述:
输入:样本集
D
=
{
x
1
,
x
2
,
.
.
.
,
x
N
}
;
D=\{\pmb x_1,\pmb x_2,...,\pmb x_N\};
D={xx1?,xx2?,...,xxN?};聚类簇数
k
.
k.
k.
过程:
??
1
:
从
D
中随机选择
k
个样本作为初始均值向量
{
μ
1
,
μ
2
,
.
.
.
,
μ
k
}
\ \ 1:从D中随机选择k个样本作为初始均值向量\{\pmb \mu_1, \pmb \mu_2,...,\pmb \mu_k\}
??1:从D中随机选择k个样本作为初始均值向量{μμ1?,μμ2?,...,μμk?}
??
2
:
repeat
\ \ 2:\texttt{repeat}
??2:repeat
??
3
:
令
C
i
=
?
(
1
≤
i
≤
k
)
\ \ 3:\hspace{0.5cm}令C_i=\varnothing(1\le i \le k)
??3:令Ci?=?(1≤i≤k)
??
4
:
for
j
=
1
,
2
,
.
.
.
,
N
do
\ \ 4:\hspace{0.5cm}\texttt{for}\hspace{0.2cm} j=1,2,...,N \hspace{0.2cm}\texttt{do}
??4:forj=1,2,...,Ndo
??
5
:
计算样本
x
j
与各均值向量
μ
i
(
1
≤
i
≤
k
)
的距离:
d
j
i
=
∣
∣
x
?
μ
i
∣
∣
2
;
\ \ 5:\hspace{1.0cm}计算样本\pmb x_j与各均值向量\pmb \mu_i(1\le i \le k)的距离:d_{ji}=||\pmb x-\pmb\mu_i||_2;
??5:计算样本xxj?与各均值向量μμi?(1≤i≤k)的距离:dji?=∣∣xx?μμi?∣∣2?;
??
6
:
根据距离最近的均值向量确定
x
j
的簇标记
:
λ
j
=
argmin
i
∈
{
1
,
2
,
.
.
.
,
k
}
d
j
i
;
\ \ 6:\hspace{1.0cm}根据距离最近的均值向量确定x_j的簇标记:\lambda_j=\texttt{argmin}_{i\in \{1,2,...,k\}}d_{ji};
??6:根据距离最近的均值向量确定xj?的簇标记:λj?=argmini∈{1,2,...,k}?dji?;
??
7
:
将样本
x
j
划入相应的簇
:
C
λ
j
=
C
λ
j
∪
{
x
j
}
;
\ \ 7:\hspace{1.0cm}将样本\pmb x_j划入相应的簇:C_{\lambda_j}=C_{\lambda_j}\cup\{\pmb x_j\};
??7:将样本xxj?划入相应的簇:Cλj??=Cλj??∪{xxj?};
??
8
:
end
?
for
\ \ 8:\hspace{0.5cm}\texttt{end for}
??8:end?for
??
9
:
for
i
=
1
,
2
,
.
.
.
,
k
do
\ \ 9:\hspace{0.5cm}\texttt{for}\hspace{0.2cm}i=1,2,...,k\hspace{0.2cm}\texttt{do}
??9:fori=1,2,...,kdo
10
:
计算新均值向量
:
μ
i
′
=
1
∣
C
i
∣
∑
x
∈
C
i
x
;
10:\hspace{1.0cm}计算新均值向量:\pmb \mu_i^{'}=\frac{1}{|C_i|}\sum_{x \in C_i}\pmb x;
10:计算新均值向量:μμi′?=∣Ci?∣1?∑x∈Ci??xx;
11
:
if
μ
i
′
≠
μ
i
then
11:\hspace{1.0cm}\texttt{if} \hspace{0.2cm}\pmb \mu_i^{'}\neq\pmb \mu_i\hspace{0.2cm}\texttt{then}
11:ifμμi′?=μμi?then
12
:
将当前均值向量
μ
i
更新为
μ
i
′
12:\hspace{1.5cm}将当前均值向量\pmb \mu_i更新为\pmb \mu_i^{'}
12:将当前均值向量μμi?更新为μμi′?
13
:
else
13:\hspace{1.0cm}\texttt{else}
13:else
14
:
保持当前均值向量不变
14:\hspace{1.5cm}保持当前均值向量不变
14:保持当前均值向量不变
15
:
end
?
if
15:\hspace{1.0cm}\texttt{end if}
15:end?if
16
:
end
?
for
16:\hspace{0.5cm}\texttt{end for}
16:end?for
17
:
until
当前均值向量均未更新
17:\texttt{until}\hspace{0.2cm}当前均值向量均未更新
17:until当前均值向量均未更新
输出:簇划分
C
=
{
C
1
,
C
2
,
.
.
.
,
C
k
}
\mathcal{C}=\{C_1,C_2,...,C_k\}
C={C1?,C2?,...,Ck?}
如果不想看上述伪代码,KMeans的主要流程可以用文字描述如下:
(0)在
N
N
N个样本中随机选择
k
k
k个样本作为初始的聚类中心;
(1)根据当前的聚类中心,重新划分每个样本所属的类;
(2)计算划分后每个类的均值向量;
(3)若均值向量已经收敛(如:变化量小于一个事先定好的阈值)或迭代次数达到给定上限,输出;否则返回(1).
下面我们仍用numpy和matplotlib库完成该实验。首先是获取数据集:
'''
返回(data, target)二元组,data为数据, target为数据所属类, data的第i行对应target第i行。
- mu: 每个类的均值, 大小为(k, d)
- sigma: 每个类的协方差, 大小为 (k, d, d)
- pi: 类先验, 大小为(k)
- N: 数据量
其中k为类数,d为数据维数。
一个合法的例子:
mu = [[1, 1], [5, 5], [3, 0]]
sigma = [[[1, 0], [0, 1]], [[2, 0], [0, 2]], [[1, 0], [0, 1]]]
pi = [0.3, 0.4, 0.3]
数据为二维,其中第一类的均值为(1, 1), 协方差矩阵为单位阵,类先验为0.3(占数据总量30%)
'''
import numpy as np
def get_dataset(mu, sigma, pi, N = 100):
eps = 1e-8
mu = np.array(mu, dtype = 'float')
sigma = np.array(sigma, dtype = 'float')
pi = np.array(pi, dtype = 'float')
assert len(mu) == len(sigma) and len(pi) == len(sigma), '参数错误!'
assert abs(np.sum(pi) - 1) < eps, '先验之和应为1!'
data = []
target = []
for index, (m, s, p) in enumerate(zip(mu, sigma, pi)):
n = N * p
# 生成 Ni=(数据总量N*类i的先验概率πi)个数据
data.append(np.random.multivariate_normal(m, s, int(n)))
# 同时把该类的类别放入target中(Ni个)
target.append(index * np.ones(int(n)))
# 把刚才生成的data和target整合到一个数组中去
# 刚才生成的形如data = [[[1, 1]], [[2, 2]], [[3, 3]]], target = [[0], [1], [2]]
# 整合后: data = [[1, 1], [2, 2], [3, 3]], target = [0, 1, 2]
data = np.array([x for lst in data for x in lst])
target = np.array([x for lst in target for x in lst])
return data, target
然后我们编写KMeans算法:
import random
import numpy as np
'''
KMeans算法。返回的clusters中,clusters[i]表示属于第i类的样本,
如cluster = [[[1, 1], [1, 2], [2, 1]], [[7, 8], [6, 7], [8, 9]]]
表示第0类中的样本为[1, 1], [1, 2]和[2, 1]; 第1类样本为[7, 8], [6, 7]和[8, 9].
- dataset: 数据集
- k: 分类数
- max_iteration: 最大迭代次数,默认为10000
'''
def KMeans(dataset, k, max_iteration = 10000):
# 收敛阈值
eps = 1e-10
# random.sample在dataset中随机抽取k个,对应伪代码第1行
mean_vectors = random.sample(list(dataset), k)
for i in range(max_iteration):
delta = 0 # 均值向量改变量
clusters = [] # clusters[i]表示当前迭代轮次中,第i类的所有样本
for i in range(k):
clusters.append([])
for x in dataset:
# 对于每个样本,计算其所属的类,详细说明见下文,对应伪代码第6行
c = np.argmin(
list(map(lambda vec: np.linalg.norm(x - vec, ord = 2), mean_vectors))
)
# 把x放入该类中
clusters[c].append(x)
# 重新计算每个类的均值向量
for i in range(k):
new_vector = np.mean(clusters[i], axis = 0)
# 累加改变量,用于判断收敛
delta += np.linalg.norm(mean_vectors[i] - new_vector)
# 更新均值向量
mean_vectors[i] = new_vector
if delta < eps: # 已经收敛
break
return clusters
代码中只有一行不是那么简洁明了:c = np.argmin(list(map(lambda vec: np.linalg.norm(x - vec, ord = 2), mean_vectors))).这行代码用于计算x所属的类。我们从里往外看:
(1)list(map(f, lst))将函数f依次作用到lst的所有元素上,返回结果的列表,这里f可以是函数名或lambda表达式。比如,当f(x)=2x(或写成lambda表达式:lambda x: 2 * x),list(map(f, [1, 2, 3]))返回[2, 4, 6].
(2)在这里,我们想计算x和每个均值向量的距离,所以我们取定lst=mean_vectors;然后对每个mean_vectors中的均值向量vec,计算x与vec的距离np.linalg.norm(x - vec)。这里可选参数norm=2可以不写。组合一下就是list(map(lambda vec: np.linalg.norm(x - vec, ord = 2), mean_vectors));
(3)np.argmin(lst)返回lst中最小元素的下标。我们已经求出了x与所有均值向量的距离数组,只需要用argmin作用一下就可以求得最小下标,该下标c即np.argmin(list(map(lambda vec: np.linalg.norm(x - vec, ord = 2), mean_vectors))).
实验的主要部分已经编写完,下面我们运行KMeans并将其可视化。主函数如下:
import matplotlib.pyplot as plt
mu = [[1, 1], [5, 5], [3, 0]]
sigma = [[[1, 0], [0, 1]], [[2, 0], [0, 2]], [[1, 0], [0, 1]]]
pi = [0.3, 0.4, 0.3]
data, target = get_dataset(mu, sigma, pi)
clusters = KMeans(data, 3)
colors = ['red', 'green', 'blue']
for i, col in enumerate(colors):
for x in clusters[i]:
# s=30: 让点大一些
plt.scatter(x[0], x[1], color = col, s = 30)
for x, y in zip(data, target):
# 用'.', 'x', '*'三种标记表示真实类别
plt.scatter(x[0], x[1], marker=('x' if y == 0 else '.' if y == 1 else '*'), color = 'white')
plt.show()
运行结果如下图所示。
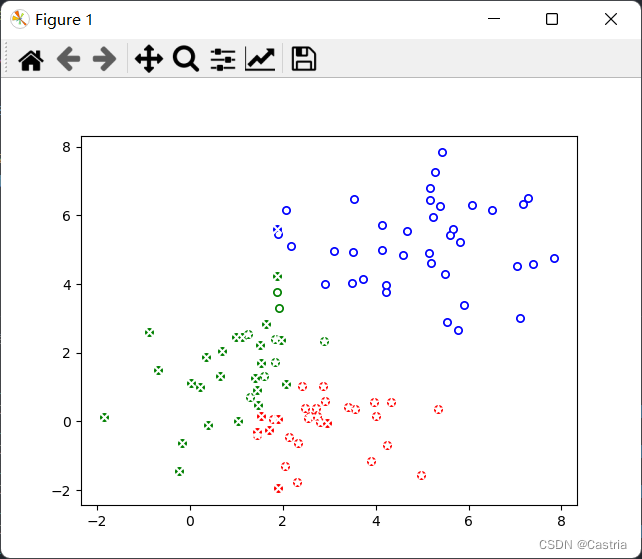
图中每个点的颜色表示KMeans聚类的结果,红/绿/蓝分别为第0/1/2类;点上面白色的标记为其真实类别。如果颜色和标记重合度比较高,说明聚类效果比较好。我们可以看到,蓝色点与圆形标记相关联;绿色点与十字标记高度关联;红色点与星形标记高度相关;同时在红绿交界处聚类发生错误的情况较多。总体上来看,KMeans能够较好地发现(正态分布)数据中隐藏的类别信息。(但与GMM相比,它无法给出准确的参数)
实验四:PCA
该实验要求用PCA(主成分分析)对高维数据进行降维。我们在这里仅给出PCA的算法步骤,理论推导在文章开篇的链接中。PCA步骤如下:
1.
将原始数据矩阵
R
d
×
N
标准化
:
x
i
j
=
r
i
j
?
r
i
ˉ
,
得到矩阵
X
;
(
R
的每一列是一个样本
)
1. 将原始数据矩阵R_{d \times N}标准化:x_{ij}=r_{ij}-\bar{r_i},得到矩阵X;(R的每一列是一个样本)
1.将原始数据矩阵Rd×N?标准化:xij?=rij??ri?ˉ?,得到矩阵X;(R的每一列是一个样本)
2.
求
X
的协方差矩阵
D
(
X
)
;
2.求X的协方差矩阵D(X);
2.求X的协方差矩阵D(X);
3.
求
D
(
X
)
的特征值
λ
1
.
.
.
λ
d
和将其相似对角化需要的正交矩阵
P
;
3.求D(X)的特征值\lambda_1...\lambda_d和将其相似对角化需要的正交矩阵P;
3.求D(X)的特征值λ1?...λd?和将其相似对角化需要的正交矩阵P;
4.
方差第
i
大的主成分系数即第
i
大特征值对应的(单位化了的)特征向量
.
4.方差第i大的主成分系数即第i大特征值对应的(单位化了的)特征向量.
4.方差第i大的主成分系数即第i大特征值对应的(单位化了的)特征向量.
其中第1步中,可以除以样本标准差;但是在之前的博客中发现sklearn的PCA模块似乎没有做这一步,我们这里以sklearn的做法为准。
此外,我们在
d
d
d个主成分中只选取方差最大
k
k
k个来降维,若设这
k
k
k个主成分的特征向量组成的矩阵为
A
=
(
α
1
,
α
2
,
.
.
.
,
α
k
)
d
×
k
A=(\pmb\alpha_1,\pmb\alpha_2,...,\pmb\alpha_k)_{d\times k}
A=(αα1?,αα2?,...,ααk?)d×k?,为了将
d
d
d维样本
x
=
(
x
1
,
x
2
,
.
.
.
,
x
d
)
\pmb x=(x_1,x_2,...,x_d)
xx=(x1?,x2?,...,xd?)降成
k
k
k维,我们只需要计算
z
=
(
x
?
μ
)
A
\pmb z=(\pmb x-\pmb \mu)A
zz=(xx?μμ)A即可,其中
μ
\pmb\mu
μμ为训练时所有样本的均值(由于标准化时减去了均值再求取主成分,所以在变换时我们也应该减去该均值)。为了将其降维后的样本还原,计算
x
′
=
z
A
T
+
μ
.
\pmb x'=\pmb zA^T+\pmb \mu.
xx′=zzAT+μμ.(在
k
=
d
k=d
k=d时,这是一个可逆变换,没有信息损失,由于
A
A
A此时为正交矩阵,
A
?
1
=
A
T
A^{-1}=A^T
A?1=AT;可以理解,在
k
<
d
k<d
k<d时逆变换仍为该形式,但会损失一些原有数据,我们在这里不讨论数学细节)
下面实现上述过程,对代码的说明详见注释:
class PCA(object):
'''
求出最大的数个主成分所对应下标。可以用参数threshold和K控制选取多少。
- X: 标准化后的特征值数组
- threshold: 若方差累计率到达threshold,停止取后面的主成分
- K: 若 K != 0, 选取至多K个主成分
'''
def __topK(self, X, threshold, K = 0):
lst = [(value, index) for index, value in enumerate(X)]
# 把(特征值, 下标)按特征值从大到小排序
lst.sort(reverse = True)
ret = []
sum = 0
for i, (value, index) in enumerate(lst):
ret.append(index)
sum += value
# 若方差贡献率合计达到threshold或限制取K个主成分,break
if (K != 0 and i == K - 1) or sum >= threshold:
break
return ret
'''
用数据集求取主成分。
- dataset: 数据集
- var: 在方差贡献率达到var后停止取主成分
- K: 至多取K个主成分
'''
def fit(self, dataset, var = 0.8, K = 5):
# 均值
self._mean = np.mean(dataset, axis = 0)
# 维度d
self.dim = len(self._mean)
# 减去均值并标准化。转置是为了与前文保持一致(每一列是一个样本)
self.dataset = np.matrix(dataset - self._mean.reshape(1, self.dim), dtype='float64').T
# 求取协方差矩阵
Cov = np.cov(self.dataset)
# 特征值, 特征向量
self.eigs, self.vectors = linalg.eig(Cov)
# 把特征值归一化,变为方差贡献率(详见之前的博客)
self.eigs /= np.sum(self.eigs)
# 方差贡献率达到0.8,或主成分达到3个时停止选取。
# self.dims是一个数组,表示最大的K个特征值对应特征向量在self.vectors中的下标
# 如 self.vectors = [v0, v1, v2, v3], self.dims可以为[0, 2, 3]
# 表示第0, 2, 3个特征值是最大的3个
self.dims = self.__topK(self.eigs, var, K)
def transform(self, x):
x = np.array(x, dtype = 'float')
# 与前文表达式一致
# self.vectors[:, self.dims]选取self.dims对应的列,组成新矩阵;
# 如 self.vectors = [v0, v1, v2, v3], self.dims为[0, 2, 3]
# 那么self.vectors[:, self.dims]返回矩阵[v0, v2, v3]
return np.dot(x - self._mean, self.vectors[:, self.dims])
def inverse_transform(self, z):
# 与前文表达式一致
return np.dot(z, self.vectors[:, self.dims].T) + self._mean
之后我们用数据来测试一下PCA降维的效果。我们首先生成一个二维数据,便于可视化。我们生成一个均值为 ( 3 , 3 ) (3,3) (3,3),协方差矩阵为 ( 10 3 3 1 ) \begin{pmatrix}10 & 3\\ 3 &1\end{pmatrix} (103?31?)的 100 100 100个点的二维正态分布,代码和图像如下:
X = np.random.multivariate_normal((3, 3), [[10, 3], [3, 1]], 100)
for x, y in X:
plt.scatter(x, y)
plt.xlim(-3, 9)
plt.ylim(-3, 9)
plt.show()
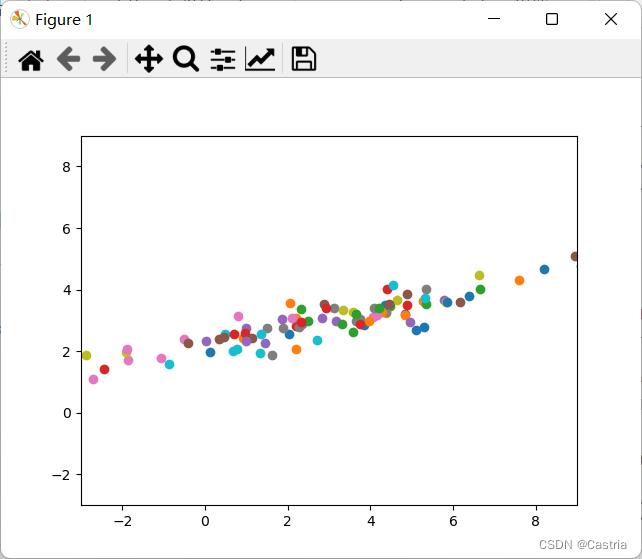
显然
x
x
x和
y
y
y具有极强的相关性(二者相关系数
ρ
=
C
o
v
(
X
,
Y
)
D
(
X
)
D
(
Y
)
=
0.949
\rho=\frac{Cov(X,Y)}{\sqrt{D(X)D(Y)}}=0.949
ρ=D(X)D(Y)?Cov(X,Y)?=0.949);通过旋转,可以使得数据在新的某一坐标轴上方差很大。我们利用刚才的PCA类对数据
(
3
,
3
)
(3, 3)
(3,3)进行降维:
X = np.random.multivariate_normal((3, 3), [[10, 3], [3, 1]], 100)
pca = PCA()
pca.fit(X)
x = [3, 3]
z = pca.transform(x)
x_ = pca.inverse_transform(z)
print(f'原始值: {x}, 降维后: {z}, 降维并还原后的值: {x_}')
结果:
原始值: [3, 3], 降维后: [0.24917721], 降维并还原后的值: [2.97314899 3.08498994]
可以看到通过PCA逆变换得到的向量与原始向量非常接近。这样,我们就用一维实数代替了原先的二维向量,同时又可以将其逆变换为与原来近似的值。(前提是数据内部具有一定的规律,即可以通过旋转使某一维具有较大的方差。若数据近似于噪声,我们很难把维度显著降低)
我们再看一个更加实际的例子:用PCA对人脸数据集进行降维。ppt上CBCL database的
2429
2429
2429张
19
×
19
19\times19
19×19灰度图像数据集在官网上似乎已经停止维护(http://poggio-lab.mit.edu/codedatasets),还好还留有另一个人脸数据集(下载地址:http://cbcl.mit.edu/software-datasets/heisele/facerecognition-database.html)。但是该数据集每张人脸是
200
×
200
200 \times 200
200×200的,转化为灰度图像一个样本就是
40000
40000
40000维,PCA计算过程中的协方差矩阵就是
40000
×
400008
b
i
t
≈
1.6
G
B
40000\times400008bit≈1.6GB
40000×400008bit≈1.6GB,计算过程还需要消耗大量额外内存。为了便于实验,我把这些数据都resize成了
19
×
19
19\times19
19×19的版本(也就是
361
361
361维,可以接受),这里提供下载,可以解压后放到项目文件夹下。我们使用python的opencv库进行图像处理。对目录中第一张图片进行降维的代码如下:
import os, cv2
import numpy as np
data = []
images = os.listdir('./train2')
for filename in images:
image = cv2.imread('./train2/' + filename, cv2.IMREAD_GRAYSCALE)
data.append(np.array(image.flatten()))
pca = PCA()
pca.fit(data)
image0 = cv2.imread('./train2/' + images[0], cv2.IMREAD_GRAYSCALE)
z = pca.transform(image0.flatten())
print(f'压缩后的向量: {z}')
image1 = np.matrix(pca.inverse_transform(z).reshape(19, 19), dtype = 'uint8')
# 拼接降维前后两张图像
cv2.imshow('image', np.hstack([image0, image1]))
cv2.waitKey(0)
运行结果:
压缩后的向量: [-237.3923432 -135.15952147 -265.03957286]

(左为压缩前,右为压缩后。虽然图像很小,但能看出右边稍微模糊了一点)
如果调整fit方法中的可选参数,比如var=0.99,K=30时,图像如下:

可以看到图片明显清晰了一些。如果用均方信噪比
S
N
R
=
10
lg
?
∑
i
,
j
f
[
i
]
[
j
]
2
∑
i
,
j
(
f
[
i
]
[
j
]
?
g
[
i
]
[
j
]
)
2
(
f
,
g
分别表示降噪前后图像矩阵
)
SNR=10\lg\frac{\sum\limits_{i,j}f[i][j]^2}{\sum\limits_{i,j}(f[i][j]-g[i][j])^2}(f,g分别表示降噪前后图像矩阵)
SNR=10lgi,j∑?(f[i][j]?g[i][j])2i,j∑?f[i][j]2?(f,g分别表示降噪前后图像矩阵)衡量,我们可以得到保留主成分更多的图像的信噪比更大,看起来也就更清晰:
def SNR(src_img, res_img):
t1 = np.sum(res_img ** 2)
t2 = np.sum((src_img - res_img) ** 2)
return 10 * (np.log10(t1) - np.log10(t2))
# ...(之前的代码)
print('信噪比:', SNR(image0, image1))
下面是以不同的K运行的结果:
(K=3)信噪比: 1.2320396558864388
(K=10)信噪比: 1.3006828992559338
(K=30)信噪比: 1.4311794216101248