[人工智能] AI 人工智能学习之聚类分析及算法(2)

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> AI 人工智能学习之聚类分析及算法(2) -> 正文阅读

[人工智能]AI 人工智能学习之聚类分析及算法(2)

聚类

聚类(Clustering)是按照某个特定标准(如距离)把一个数据集分割成不同的类或簇，使得同一个簇内的数据对象的相似性尽可能大，同时不在同一个簇中的数据对象的差异性也尽可能地大。也即聚类后同一类的数据尽可能聚集到一起，不同类数据尽量分离。

聚类是指把相似的数据划分到一起，具体划分的时候并不关心这一类的标签，目标就是把相似的数据聚合到一起。

聚类算法
聚类算法，它是研究（样品或指标）分类问题的一种统计分析方法，同时也是数据挖掘的一个重要算法。另外需要说明的是，聚类是以相似性为基础的。

k均值聚类是最著名的划分聚类算法，由于简洁和效率使得他成为所有聚类算法中最广泛使用的。给定一个数据点集合和需要的聚类数目k，k由用户指定，k均值算法根据某个距离函数反复把数据分入k个聚类中。

kmeans算法

划分聚类（partition based clustering）：给定包含N个点的数据集，划分法将构造K个分组；每个分组代表一个聚类，这里每个分组至少包含一个数据点，每个数据点属于且只属于一个分组；对于给定的K值，算法先给出一个初始化的分组方法，然后通过反复迭代的的方法改变分组，知道准则函数收敛。

K-means算法是输入聚类个数k，以及包含 n个数据对象的数据库，输出满足方差最小标准的k个聚类。
k-means 算法接受输入量 k ；然后将n个数据对象划分为 k个聚类以便使得所获得的聚类满足：同一聚类中的对象相似度较高；而不同聚类中的对象相似度较小。聚类相似度是利用各聚类中对象的均值所获得一个“中心对象”（引力中心）来进行计算的。

算法定义：

给定样本集： $D=\begin{Bmatrix} \vec{x_{1}},&\vec{x_{2}}, & ... & \vec{x_{m}}, \end{Bmatrix}$ ，?k均值算法针对聚类所得簇： $C=\begin{Bmatrix} C_{1} ,& C_{2} , & ..., & C_{k} \end{Bmatrix}$

最小化平方差： $E=\sum_{i=1}^{k}\sum_{x\in C_{i}}^{}|| \vec{x}-\mu _{i}||_{2}^{2}$ ,其中： $\mu _{i}=\frac{1}{C} \sum_{x\in C_{i}}^{}\vec{x}$ ?簇? $C_{i}$ 的质心，上面的2代表平方，下面的2代表范数2。

k-means 算法基本步骤
a.首先确定一个k值，即希望将数据集经过聚类得到k个集合
b.从数据集中随机选取K个数据点作为初始的聚类中心
b.对数据集中每一个点，计算其与每一个质心的距离（如欧式距离），离哪个质心近，就划分到哪个质心所属的集合。
c.把所有数据归好集合后，一共有k个集合。然后重新计算每个集合的质心。
这个过程不断重复，直到准则函数（误差的平方和SSE作为全局的目标函数）收敛，直到质心不发生明显的变化。

优点：

简单直观，抑郁理解实现；
复杂度相对比较低，在K不是很大的情况下，Kmeans的计算时间相对很短；
Kmean会产生紧密度比较高的簇，反映了簇内样本围绕质心的紧密程度的一种算法。

缺点：

很难预测到准确的簇的数目；
对初始值设置很敏感（Kmeans++）；
Kmeans主要发现圆形或者球形簇，对不同形状和密度的簇效果不好；
Kmeans对噪声和离群值非常敏感（Kmeadians对噪声和离群值不敏感）

DBSCAN聚类算法

DBSCAN是基于密度的聚类算法，核心思想为将数据集的各密集区域当做一个一个的聚类簇。BSCAN算法的显著优点是聚类速度快且能够有效处理噪声点和发现任意形状的空间聚类。DBSCAN基于密度，它可以找到样本点的全部密集区域，并把这些密集区域当做一个一个的聚类簇。

DBSCAN算法基于点的密度而不是点之间的距离，此外它也不要求我们指定集群的数量，不仅有效避免了异常值，并且在任意形状和大小的集群上都具有非常好的聚类效果。DBSCAN 算法中有两个重要参数：Eps 和 MmPtS。Eps 是定义密度时的邻域半径，MmPts 为定义核心点时的阈值。

算法原理：

DBSCAN通过检查数据集中每个点的r邻域来搜索簇，如果点p的r邻域包含多于MinPts个点，则创建一个以p为核心对象的簇；
然后， DBSCAN迭代的聚集从这些核心对象直接密度可达的对象，这个过程可能涉及一些密度可达簇的合并；
当没有新的带你添加到任何簇时，迭代过程结束。

算法参数?

半径(epsilon)：计算的最大半径（epsilon?）。如果数据点的相互距离小于或等于指定的epsilon，那么它们在同一邻域。换句话说，它是DBSCAN用来确定两个点是否相似和属于同一类的距离。更大的epsilon将产生更大的簇（包含更多的数据点），更小的epsilon将构建更小的簇。

最小点(minpts)：在一个邻域内，点的最小数量。这些点被认为是一个簇。这里要特别注意，初始点包含在minpts中。一个较低的minpts帮助算法建立更多的集群与更多的噪声或离群值。较高的minpts将确保更健壮的集群，但如果集群太大，较小的集群将被合并到较大的集群中。

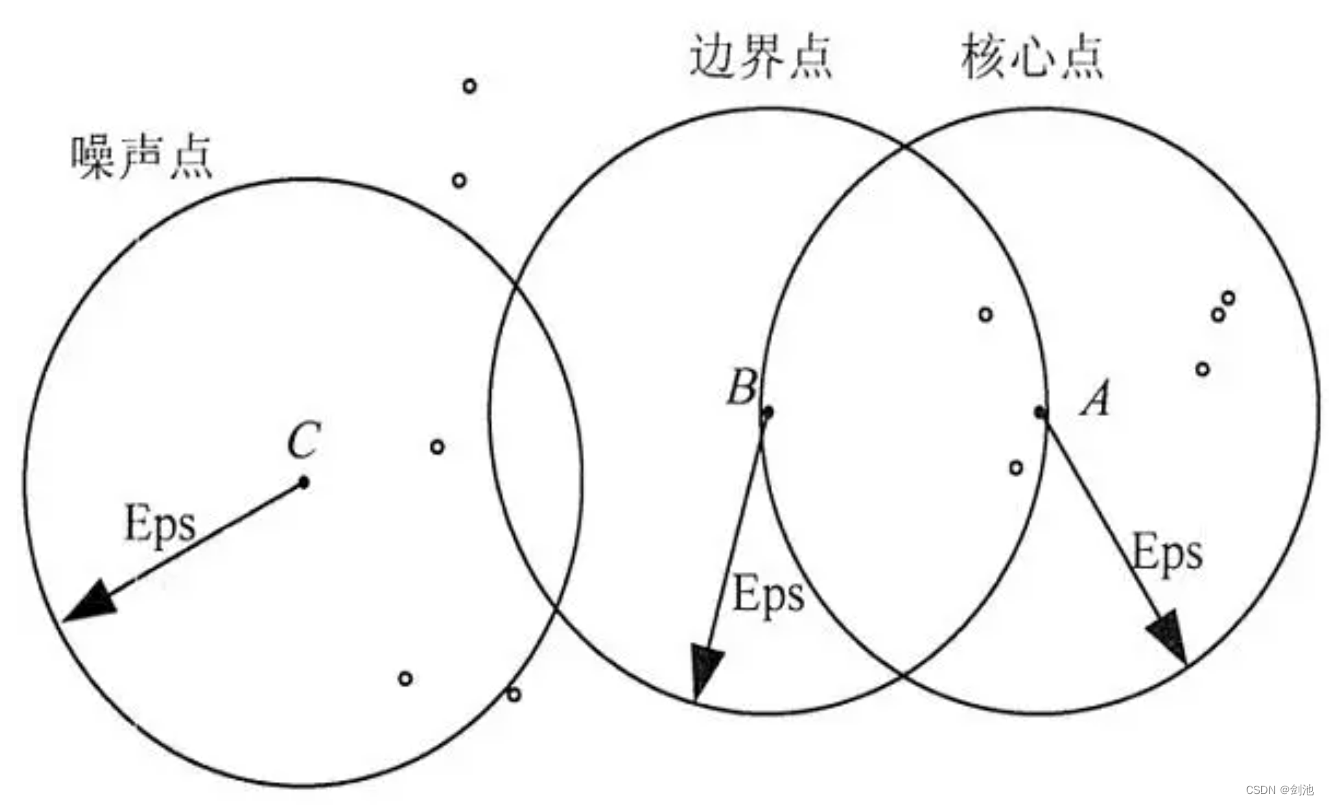
核心点：以该点为圆心，如果给定半径epsilon内含有大于等于minpts数目的点，那么该点就是核心点。

边界点：以该点为圆心，如果给定半径epsilon内含有不超过minpts数目的点，并且落在核心点的epsilon半径内。

噪声点：不是核心点也不是边界点的点。

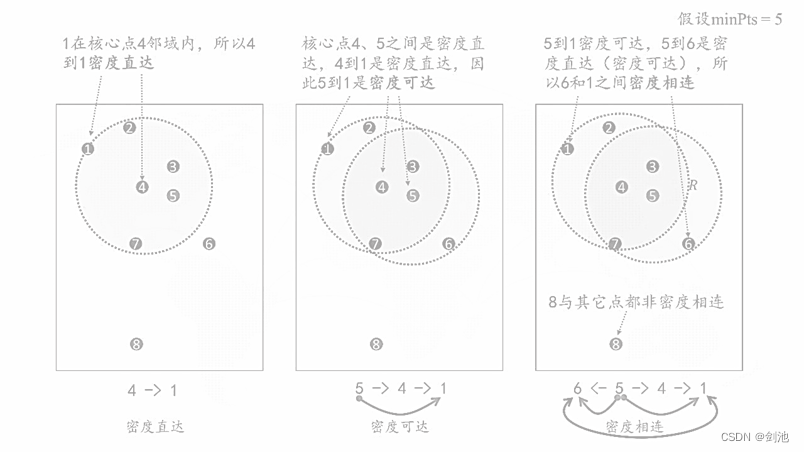
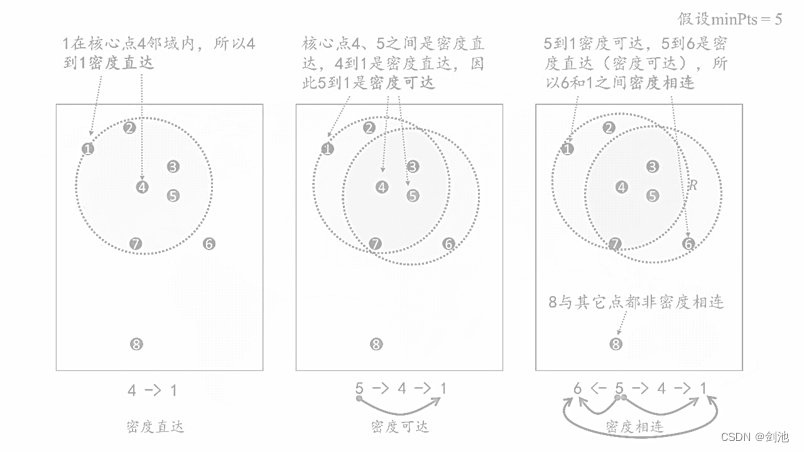
密度直达：如果P为核心点，Q在P的邻域内，那么称P到Q密度直达。反之不一定成立，即此时不能说Q到P密度直达，除非Q也是核心点，即密度直达不满足对称性。

如上图左，4为核心点，1在4的邻域内，那么4到1密度直达。

密度可达：如果存在核心点P2,P3,......,Pn,并且P1到P2密度直达，P2到P3密度直达，......,Pn-1到Pn密度直达，Pn到Q密度直达，则P1到Q密度可达。密度可达也不具备对称性。

如上图中，4、5为核心点，1在4的邻域内，4到1密度直达。那么5到1密度可达。

密度相连：如果存在核心点S，使得S到P和Q都密度可达，则P和Q密度相连。密度相连具有对称性，如果P和Q密度相连，那么Q和P也一定密度相连。密度相连的连个点属于同一聚类簇。

如上图右，4、5为核心点，1在4的邻域内，6在5邻域内，5到1密度可达，5到6密度直达，所以6和1之间密度相连。

非密度相连：如果两个点不属于密度相连关系，则两个点非密度相连。非密度相连的两个点属于不同的聚类簇，或者其中存在噪声点。如上图右，8与其它点都非密度相连。

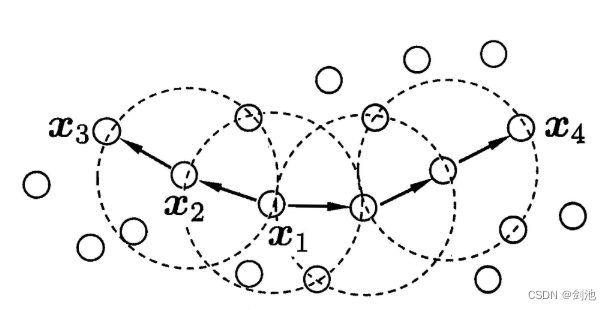
当minPts=3时，虚线圈表示ε邻域，则从下图中DD可以观察到：

x1是核心对象；
x2由x1密度直达；
x3由x1密度可达；
x3与x4密度相连。

ε邻域使用（ε，minpts）这两个关键的参数来描述邻域样本分布的紧密程度，规定了在一定邻域阈值内样本的个数（类似密度的概念）

算法优缺点

优点：

不需要人工设定k值
可以对任意形状的稠密数据集进行聚类
可以在聚类的同时发现异常点，对数据集中的异常点不敏感

缺点：

如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差，这时用DBSCAN聚类一般不适合。
主要需要对距离阈值?，邻域样本数阈值MinPts联合调参，不同的参数组合对最后的聚类效果有较大影响。一般这两个参数的确定靠经验值。如果觉得经验值聚类的结果不满意，可以适当调整?和MinPts的值，经过多次迭代计算对比，选择最合适的参数值。
不适合高维数据，可以先进行降维操作
Sklearn中效率很慢，可以先执行数据削减策略

聚类评估

轮廓系数

聚类效果好坏的一种评价方式。它结合内聚度和分离度两种因素。可以用来在相同原始数据的基础上用来评价不同算法、或者算法不同运行方式对聚类结果所产生的影响。

好的聚类一般内密外疏，同一个聚类内部的样本要足够密集，不同聚类之间样本要足够疏远。

针对样本空间中的一个特定样本，计算它与所在聚类其它样本的平均距离a，以及该样本与距离最近的另一个聚类中所有样本的平均距离b，该样本的轮廓系数为(b-a)/max(a, b)，将整个样本空间中所有样本的轮廓系数取算数平均值，作为聚类划分的性能指标s。
轮廓系数的区间为：[-1, 1]。 -1代表分类效果差，1代表分类效果好。0代表聚类重叠，没有很好的划分聚类。

针对某个样本的轮廓系数s为：

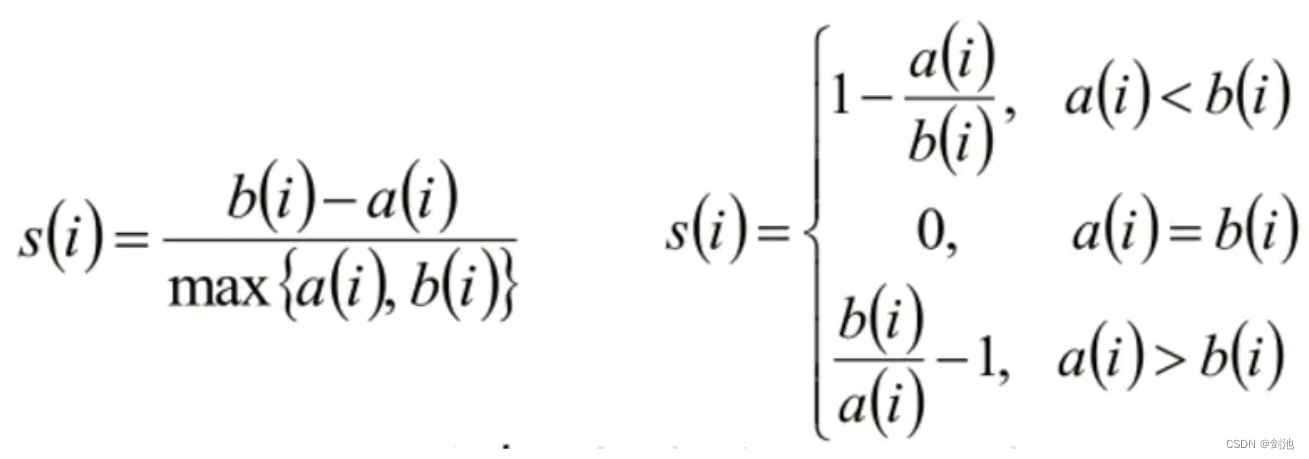
计算样本i到同簇其他样本的平均距离 $a_{i}$ ， $a_{i}$ 越小，说明样本i越应该被聚类到该簇。将 $a_{i}$ 成为样本i的簇内不相似度。
计算样本i到其他某簇 $C_{j}$ 的所有样本的平均距离 $b_{ij}$ ，称为样本i与簇 $c_{j}$ 的不相似度。定义为样本i的簇间不相似度： $b_{i}=min\begin{Bmatrix} b_{i1}, & b_{i2}, & ..., & b_{ik} \end{Bmatrix}$
$s_{i}$ 接近1，则说明样本i聚类合理。
$s_{i}$ 接近-1，则说明样本i更应该分类到另外的簇。
若 $s_{i}$ 近似为0，则说明样本i在两个簇的边界上。