🚀 优质资源分享 🚀
| 学习路线指引(点击解锁) | 知识定位 | 人群定位 |
|---|---|---|
| 🧡 Python实战微信订餐小程序 🧡 | 进阶级 | 本课程是python flask+微信小程序的完美结合,从项目搭建到腾讯云部署上线,打造一个全栈订餐系统。 |
| 💛Python量化交易实战💛 | 入门级 | 手把手带你打造一个易扩展、更安全、效率更高的量化交易系统 |
| 目录 |
回到顶部## 0 引言
大多数分割算法都基于图像灰度值的两个基本性质之一:不连续性和相似性。第一类方法根据灰度的突变(如边缘)将图像分割为多个区域:首先寻找边缘线段,然后将这些线段连接为边界的方法来识别区域。第二类方法根据一组预定义的准则把一幅图像分割为多个区域。本节讨论两种相关的区域分割方法:(1)在数据中寻找聚类的经典方法,它与亮度和颜色等变量有关;(2)用聚类从图像中提取“超像素”的现代方法。

回到顶部## 1 使用k均值聚类的区域分割
1.1 原理
**聚类方法的思想****是将样本集合按照其特征的相似性划分为若干类别,使同一类别样本的特征具有较高的相似性,不同类别样本的特征具有较大的差异性。**令{z1, z2, z3 …, zn}是样本集合,在图像分割中,样本向量z的每个分量表示一个数值像素属性。例如,分割只基于灰度尺度时,z是一个表示像素灰度的标量。分割的如果是RGB彩色图像,z通常是一个三维向量,这个三维向量的每个分量是RGB三通道的灰度值。k均值聚类的目的就是将样本集合划分为k个满足如下最优准则的不相交的聚类集合C={C1, C2, …, Ck}:
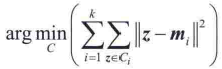
式中,mi是集合Ci中样本的均值向量(或质心),||z-mi||项是Ci中的一个样本到均值mi的欧式距离。换言之,这个公式说,我们感兴趣的是找到集合C={C1, C2, …, Ck},集合中的每个点到该集合的均值的距离之和是最小的。
基于聚类的区域分割,就是基于图像的灰度、颜色、纹理、形状等特征,用聚类算法把图像分成若干类别或区域,使每个点到聚类中心的均值最小。k 均值(k-means)是一种无监督聚类算法。基于 k 均值聚类算法的区域分割,算法步骤为:
(1)初始化算法:规定一组初始均值
(2)将样本分配给聚类:对所有的像素点,计算像素到每个聚类中心的距离,将像素分类到距离最小的一个聚类中;
(3)更新聚类中心:根据分类结果计算出新的聚类中心;
(4)完备性验证:计算当前步骤和前几步中平均向量之间的差的欧几里得范数。计算残差E,即k个范数之和。若E≤T,其中T是一个规定的非负阈值,则停止。否则,返回步骤2。
1.2 cv::kmeans函数
OpenCV提供了函数cv::kmeans来实现 k-means 聚类算法。函数cv::kmeans不仅可以基于灰度、颜色对图像进行区域分割,也可以基于样本的其它特征如纹理、形状进行聚类。
double cv::kmeans(InputArray data, //用于聚类的数据,类型为 CV\_32F
int K, //设定的聚类数量
InputOutputArray bestLabels, //输出整数数组,用于存储每个样本的聚类类别索引
TermCriteria criteria, //算法终止条件:即最大迭代次数或所需精度
int attempts, //用于指定使用不同初始标记执行算法的次数
int flags, //初始化聚类中心的方法:0=随机初始化 1=kmeans++方法初始化 2=第一次用用户指定的标签初始化,后面attempts-1都用随机或版随机的初始化
OutputArray centers = noArray() //聚类中心的输出矩阵,每个聚类中心占一行
)
示例?图像分割之k均值聚类
| 123456789101112131415 | Mat src = imread(``"./14.tif"``, 0);``Mat dataPixels = src.reshape(0, 1);``//可以是一列,每一行表示一个样本;或者一行,一列是一个样本;样本的分量数为通道数``dataPixels.convertTo(dataPixels, CV_32FC1);``//输入需要是32位浮点型``int numCluster = 3;``Mat labels;``Mat centers;``kmeans(dataPixels, numCluster, labels, TermCriteria(TermCriteria::EPS + TermCriteria::COUNT, 10, 0.1), 3, KMEANS_PP_CENTERS, centers);``Mat dst = Mat::zeros(src.size(), CV_8UC1);``float``* pdata = dataPixels.ptr<``float``>(0);``for (``int i = 0; i < src.rows * src.cols; i++) {``int k = labels.ptr<``int``>(i)[0];``//每个像素对应的标签k,即属于集合k``pdata[i] = centers.ptr<``float``>(k)[0];``//用集合中心替换该像素``}``dataPixels.convertTo(dataPixels, CV_8UC1);``dst = dataPixels.reshape(0, src.rows); |
1.3 cv::kmeans源码
当图片非常大时,对图像进行简单的计算操作,耗时就会变得非常大,常用的加速方法如OpenMp,TBB,OpenCL和CUDA。使用cuda时,图片在cpu和gpu之间的传输时间就达到上百ms,不适合本来就是ms级的计算。在kmeans源码中使用**parallel_for_**并行计算各个样本到聚类中心的距离。这边写一个简单的例子,了解下parallel_for_的用法。
示例 利用并行计算加速图片旋转
| 1234567891011121314151617181920212223242526272829303132333435363738 | // 方法1:并行 将该方法写成一个类,继承ParallelLoopBody,然后重写(),利用parallel_for_可以开启并行``class trans :``public ParallelLoopBody {``public``:``trans(``const uchar* _src, uchar*_dst, int _dims, int _istep):src(_src), dst(_dst), dims(_dims), istep(_istep) {}``void operator()(``const Range& range) const //重载操作符()``{``for (``int n = range.start; n < range.end; ++n)``{``for (``int i = 0; i < dims; i++)``dst[i * istep + (istep - 1 - n)] = src[n * dims + i];``}``}``private``:``const uchar* src;``uchar* dst;``int dims;``int istep;``};``// 方法2 for循环``void rotate(Mat& src, Mat& dst, int srcWidth, int srcHeight)``{``int istep = src.step;``uchar* psrc = src.ptr();``uchar* pdst = dst.ptr();``for (``size_t i = 0; i < srcHeight; i++)``for (``size_t j = 0; j < srcWidth; j++)``pdst[j * istep + (istep-1-i)] = psrc[i * istep + j];``}?//调用``uchar* psrc = src.ptr(); uchar* pdst = dst.ptr();``int dims = src.cols;``int istep = src.step;``int N = src.rows;``rotate(src, dst, ROTATE_90_CLOCKWISE);``// opencv提供的方法 3ms``rotate(src, dst, src.cols, src.rows);``// 自己写的for循环 20ms``parallel_for_(Range(0, N), trans(psrc, pdst, dims, istep)); // 并行加速3ms |
源码位于opencv路径下sources\modules\core\src\kmeans.cpp中,首先是初始化算法:规定一组初始center,一种是随机产生,另一种是用kmeans++初始化。kmeans++初始化聚类中心是以概率的形式逐个选择聚类中心,并在选择聚类中心时,给距离较远的点更高的权重,即更容易被选择为聚类中心。假设有5个点,随机选择其中一个点为中心,计算其他点到该点的距离的平方分别为10,20,5,15。则选下一个聚类中心时它们的权值为0.2,0.4,0.1和0.3。用代码写就是,距离平方和50,在【0,50】间随机生成一个数,用这个数挨个减去10,再减去20…直到结果小于0,下一个聚类中心就是该点。
| 12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879 | // 随机产生聚类中心``// dims 样本向量的分量数``// box? 存放了所有样本中每个分量的最大值和最小值``static void generateRandomCenter(``int dims, const Vec2f* box, float``* center, RNG& rng)``{``float margin = 1.f / dims;``for (``int j = 0; j < dims; j++)``center[j] = ((``float``)rng * (1.f + margin * 2.f) - margin) * (box[j][1] - box[j][0]) + box[j][0];``}``/*``k-means center initialization using the following algorithm:``Arthur & Vassilvitskii (2007) k-means++: The Advantages of Careful Seeding``*/``static void generateCentersPP(``const Mat& data, Mat& _out_centers,``int K, RNG& rng, int trials)``{``CV_TRACE_FUNCTION();``const int dims = data.cols, N = data.rows;``cv::AutoBuffer<``int``, 64> _centers(K);``int``* centers = &_centers[0];``cv::AutoBuffer<``float``, 0> _dist(N * 3);``// 3倍样本数量大小,存不同时刻样本到最近聚类中心的距离``float``* dist = &_dist[0], * tdist = dist + N, * tdist2 = tdist + N;``double sum0 = 0;``// 第一个聚类中心随机生成``centers[0] = (unsigned)rng % N;``// %N 即可获得[0,N-1]的随机数``// 计算所有样本到第一个中心的距离,并求和``for (``int i = 0; i < N; i++)``{``dist[i] = hal::normL2Sqr_(data.ptr<``float``>(i), data.ptr<``float``>(centers[0]), dims);``sum0 += dist[i];``}``// 计算第2、3...个聚类中心,离第一个中心越远的点权重越高``for (``int k = 1; k < K; k++)``{``double bestSum = DBL_MAX;``int bestCenter = -1;?for (``int j = 0; j < trials; j++)``// 相当于随机抛硬币掉在哪个格子里,做trials次``{``double p = (``double``)rng * sum0;``//(double)rng会产生0-1的随机数``int ci = 0;``for (; ci < N - 1; ci++)``{``p -= dist[ci];``if (p <= 0)``break``;``}``//选中第ci个样本为聚类中心,计算距离,如果有样本离新聚类中心更近,距离会被更新``parallel_for_(Range(0, N),``KMeansPPDistanceComputer(tdist2, data, dist, ci),``(``double``)divUp((``size_t``)(dims * N), CV_KMEANS_PARALLEL_GRANULARITY));``double s = 0;``for (``int i = 0; i < N; i++)``//所有样本离其最近的聚类中心之和``{``s += tdist2[i];``}?if (s < bestSum)``{``bestSum = s;``bestCenter = ci;``std::swap(tdist, tdist2);``// 把总和最小的数据暂存在tdist中``}``}``if (bestCenter < 0)``CV_Error(Error::StsNoConv, "kmeans: can't update cluster center (check input for huge or NaN values)"``);``centers[k] = bestCenter;``sum0 = bestSum;``std::swap(dist, tdist);``// 把总和最小的数据从tdist放入dist``}?for (``int k = 0; k < K; k++)``// centers中存放的是聚类中心对应的样本在样本集合中的索引``{``const float``* src = data.ptr<``float``>(centers[k]);``float``* dst = _out_centers.ptr<``float``>(k);``for (``int j = 0; j < dims; j++)``dst[j] = src[j];``// 把k个聚类中心样本放到_out_centers中``}``} |
计算距离
| 1234567891011121314151617181920212223242526272829303132 | // 并行计算每个样本距离中心的距离``// dist 3倍样本数量N的autobuffer,前N个存放上次的N个距离(dist_指向第一个),后N个存放本次计算的N个距离(tdist2_指向第一个)``// data 样本向量集合``// ci?? 计算所有样本和第ci个样本的距离``class KMeansPPDistanceComputer : public ParallelLoopBody``{``public``:``KMeansPPDistanceComputer(``float``* tdist2_, const Mat& data_, const float``* dist_, int ci_) :``tdist2(tdist2_), data(data_), dist(dist_), ci(ci_)``//成员初始化列表的写法``{ }?void operator()(``const cv::Range& range) const CV_OVERRIDE``{``CV_TRACE_FUNCTION();``const int begin = range.start;``const int end = range.end;``const int dims = data.cols;?for (``int i = begin; i < end; i++)``//遍历每一行,一行为一个样本向量,一个向量有dims个分量``{``//需要计算的是每个样本到离他最近的中心的距离,通过比较上一次dist中的距离和本次的tdist2哪个更小来实现``tdist2[i] = std::min(hal::normL2Sqr_(data.ptr<``float``>(i), data.ptr<``float``>(ci), dims), dist[i]);``}``}?private``:``KMeansPPDistanceComputer& operator=(``const KMeansPPDistanceComputer&); // = delete?float``* tdist2;``const Mat& data;``const float``* dist;``const int ci;``}; |
更新标签
| 12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364 | // 并行计算每个样本到对应中心的距离,已知样本属于哪个集合,直接计算该样本到集合中心的距离``template``<``bool onlyDistance>``class KMeansDistanceComputer : public ParallelLoopBody``{``public``:``KMeansDistanceComputer(``double``* distances_,``int``* labels_,``const Mat& data_,``const Mat& centers_)``: distances(distances_),``labels(labels_),``data(data_),``centers(centers_)``{``}?void operator()(``const Range& range) const CV_OVERRIDE``{``CV_TRACE_FUNCTION();``const int begin = range.start;``const int end = range.end;``const int K = centers.rows;``const int dims = centers.cols;?for (``int i = begin; i < end; ++i)``{``const float``* sample = data.ptr<``float``>(i);``if (onlyDistance)``// 只算距离,不重新分配标签``{``const float``* center = centers.ptr<``float``>(labels[i]);``distances[i] = hal::normL2Sqr_(sample, center, dims);``continue``;``}``else // 遍历每一个样本,计算该样本到每一个中心的距离,重新分配标签``{``int k_best = 0;``double min_dist = DBL_MAX;?for (``int k = 0; k < K; k++)``{``const float``* center = centers.ptr<``float``>(k);``const double dist = hal::normL2Sqr_(sample, center, dims);?if (min_dist > dist)``{``min_dist = dist;``k_best = k;``}``}?distances[i] = min_dist;``labels[i] = k_best;``}``}``}?private``:``KMeansDistanceComputer& operator=(``const KMeansDistanceComputer&); // = delete?double``* distances;``int``* labels;``const Mat& data;``const Mat& centers;``}; |
kmeans
| 123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237 | //_data:特征向量集;K:聚类中心个数;_bestLabels:每个特征向量隶属聚类中心索引``//criteria:迭代算法终止条件;attempts:尝试次数;``//flags:第一次尝试初始化采取策略;_centers:存放聚类中心``double cv::kmeans(InputArray _data, int K,``InputOutputArray _bestLabels,``TermCriteria criteria, int attempts,``int flags, OutputArray _centers)``{``CV_INSTRUMENT_REGION();``const int SPP_TRIALS = 3;``Mat data0 = _data.getMat();``const bool isrow = data0.rows == 1;``// 输入的数据应该是一行,或者一列的,通道数是每个样本向量的分量数``const int N = isrow ? data0.cols : data0.rows;``// N表示样本向量个数``const int dims = (isrow ? 1 : data0.cols) * data0.channels();``// 每个样本向量的维度(分量数)``const int type = data0.depth();``//数据类型,应为32位浮点数?attempts = std::max(attempts, 1);``//至少尝试一次``CV_Assert(data0.dims <= 2 && type == CV_32F && K > 0);``CV_CheckGE(N, K, "Number of clusters should be more than number of elements"``);?Mat data(N, dims, CV_32F, data0.ptr(), isrow ? dims * sizeof``(``float``) : static_cast``<``size_t``>(data0.step));?_bestLabels.create(N, 1, CV_32S, -1, true``);``//_bestLabels为N*1大小矩阵,类型为32为有符号整型,每个样本向量有有一个标签?Mat _labels, best_labels = _bestLabels.getMat();``if (flags & CV_KMEANS_USE_INITIAL_LABELS) // 如果首次是由用户指定的``{``CV_Assert((best_labels.cols == 1 || best_labels.rows == 1) &&``best_labels.cols * best_labels.rows == N &&``best_labels.type() == CV_32S &&``best_labels.isContinuous());``best_labels.reshape(1, N).copyTo(_labels);``for (``int i = 0; i < N; i++)``//将内容复制到_labels中``{``CV_Assert((unsigned)_labels.at<``int``>(i) < (unsigned)K);``}``}``else //否则,创建空的_labels``{``if (!((best_labels.cols == 1 || best_labels.rows == 1) &&``best_labels.cols * best_labels.rows == N &&``best_labels.type() == CV_32S &&``best_labels.isContinuous()))``{``_bestLabels.create(N, 1, CV_32S);``best_labels = _bestLabels.getMat();``}``_labels.create(best_labels.size(), best_labels.type());``}``int``* labels = _labels.ptr<``int``>();?Mat centers(K, dims, type), old_centers(K, dims, type), temp(1, dims, type);``cv::AutoBuffer<``int``, 64> counters(K);``cv::AutoBuffer<``double``, 64> dists(N);``RNG& rng = theRNG();?if (criteria.type & TermCriteria::EPS)``//算法精度``criteria.epsilon = std::max(criteria.epsilon, 0.);``else``criteria.epsilon = FLT_EPSILON;``criteria.epsilon *= criteria.epsilon;?if (criteria.type & TermCriteria::COUNT)``//最大迭代次数``criteria.maxCount = std::min(std::max(criteria.maxCount, 2), 100);``else``criteria.maxCount = 100;?if (K == 1)``{``attempts = 1;``criteria.maxCount = 2;``}?cv::AutoBuffer box(dims);``if (!(flags & KMEANS_PP_CENTERS))``//随机初始化中心的话要计算下范围,在最大小值之间随机生成``{``{``const float``* sample = data.ptr<``float``>(0);``for (``int j = 0; j < dims; j++)``box[j] = Vec2f(sample[j], sample[j]);``}``for (``int i = 1; i < N; i++)``{``const float``* sample = data.ptr<``float``>(i);``for (``int j = 0; j < dims; j++)``{``float v = sample[j];``box[j][0] = std::min(box[j][0], v);``box[j][1] = std::max(box[j][1], v);``}``}``}?double best_compactness = DBL_MAX;``for (``int a = 0; a < attempts; a++)``//算法尝试次数为attempts次``{``double compactness = 0;?for (``int iter = 0; ;)``{``double max_center_shift = iter == 0 ? DBL_MAX : 0.0;?swap(centers, old_centers);``//循环初始,需要对centers进行初始化操作,这里主要是两种,一个是random,另一个是kmeans++算法``if (iter == 0 && (a > 0 || !(flags & KMEANS_USE_INITIAL_LABELS)))``{``if (flags & KMEANS_PP_CENTERS)``generateCentersPP(data, centers, K, rng, SPP_TRIALS);``else``{``for (``int k = 0; k < K; k++)``generateRandomCenter(dims, box.data(), centers.ptr<``float``>(k), rng);``}``}``else //若为人工指定labels,或者不是第一次迭代,将样本划分进不同的集合,根据labels``{``// compute centers``centers = Scalar(0); // 对centers进行初始化操作``for (``int k = 0; k < K; k++)``counters[k] = 0;``// 对counter进行初始化操作,统计每个集合包含样本向量个数?for (``int i = 0; i < N; i++)``// 将样本按照label分为k类,每一类计算样本值的总和、样本个数``{``const float``* sample = data.ptr<``float``>(i);``int k = labels[i];``float``* center = centers.ptr<``float``>(k);``for (``int j = 0; j < dims; j++)``center[j] += sample[j];``counters[k]++;``}?for (``int k = 0; k < K; k++)``// 遍历所有的集合,看有没有空的集合``{``if (counters[k] != 0)``continue``;?// if some cluster appeared to be empty then:``//?? 1. find the biggest cluster``//?? 2. find the farthest from the center point in the biggest cluster``//?? 3. exclude the farthest point from the biggest cluster and form a new 1-point cluster.``int max_k = 0;``for (``int k1 = 1; k1 < K; k1++)``// 1. 找最大的样本集合(counters中存放每个集合的样本数)``{``if (counters[max_k] < counters[k1])``max_k = k1;``}?double max_dist = 0;``int farthest_i = -1;``float``* base_center = centers.ptr<``float``>(max_k);``float``* _base_center = temp.ptr<``float``>(); // normalized``float scale = 1.f / counters[max_k];``for (``int j = 0; j < dims; j++)``_base_center[j] = base_center[j] * scale;?for (``int i = 0; i < N; i++)``// 2. 找最大集合中离集合最远的点``{``if (labels[i] != max_k)``continue``;``const float``* sample = data.ptr<``float``>(i);``double dist = hal::normL2Sqr_(sample, _base_center, dims);?if (max_dist <= dist)``{``max_dist = dist;``farthest_i = i;``}``}``// 3. 从最大集合中去掉这个最远点,在空集合中加入该点``counters[max_k]--;``counters[k]++;``labels[farthest_i] = k;?const float``* sample = data.ptr<``float``>(farthest_i);``float``* cur_center = centers.ptr<``float``>(k);``for (``int j = 0; j < dims; j++)``{``base_center[j] -= sample[j];``//最大集合减去该样本的值``cur_center[j] += sample[j];``//空集合加上该样本的值``}``}?for (``int k = 0; k < K; k++)``// 此时所有的集合都是有样本的``{``float``* center = centers.ptr<``float``>(k);``CV_Assert(counters[k] != 0);?float scale = 1.f / counters[k];``for (``int j = 0; j < dims; j++)``// center中是样本值的和,除以样本数量等于聚类中心``center[j] *= scale;?if (iter > 0)``// 计算本次循环和上次聚类中心的差距,差距小于criteria.epsilon则为最后一次迭代``{``double dist = 0;``const float``* old_center = old_centers.ptr<``float``>(k);``for (``int j = 0; j < dims; j++)``{``double t = center[j] - old_center[j];``dist += t * t;``}``max_center_shift = std::max(max_center_shift, dist);``}``}``}?bool isLastIter = (++iter == MAX(criteria.maxCount, 2) || max_center_shift <= criteria.epsilon);?if (isLastIter)``//是最后一次的话,就再计算下每个样本离聚类中心的距离,不重新分配标签以防出现空集合``{``// don't re-assign labels to avoid creation of empty clusters``parallel_for_(Range(0, N), KMeansDistanceComputer<``true``>(dists.data(), labels, data, centers), (``double``)divUp((``size_t``)(dims * N), CV_KMEANS_PARALLEL_GRANULARITY));``compactness = sum(Mat(Size(N, 1), CV_64F, &dists[0]))[0];``// 记录距离和``break``;``}``else // 不是最后一次的话,计算距离的同时还要重新分配下标签,可能会导致空集合``{``// assign labels``parallel_for_(Range(0, N), KMeansDistanceComputer<``false``>(dists.data(), labels, data, centers), (``double``)divUp((``size_t``)(dims * N * K), CV_KMEANS_PARALLEL_GRANULARITY));``}``}``//compactness将记录所有距离,这里的距离是指,所有的特征向量到其聚类中心的距离之和,用于评价当前的聚类结果``if (compactness < best_compactness)``{``best_compactness = compactness;``if (_centers.needed())``{``if (_centers.fixedType() && _centers.channels() == dims)``centers.reshape(dims).copyTo(_centers);``else``centers.copyTo(_centers);``}``_labels.copyTo(best_labels);``}``}?return best_compactness;``} |
回到顶部## 2 使用超像素的区域分割
超像素图像分割基于依赖于图像的颜色信息及空间关系信息,将图像分割为远超于目标个数、远小于像素数量的超像素块,达到尽可能保留图像中所有目标的边缘信息的目的,从而更好的辅助后续视觉任务(如目标检测、目标跟踪、语义分割等)。
超像素是由一系列位置相邻,颜色、亮度、纹理等特征相似的像素点组成的小区域,我们将其视为具有代表性的大“像素”,称为超像素。超像素技术通过像素的组合得到少量(相对于像素数量)具有感知意义的超像素区域,代替大量原始像素表达图像特征,可以极大地降低图像处理的复杂度、减小计算量。超像素分割的结果是覆盖整个图像的子区域的集合,或从图像中提取的轮廓线的集合。 超像素的数量越少,丧失的细节特征越多,但仍然能基本保留主要区域之间的边界及图像的基本拓扑。

常用的超像素分割方法有:简单线性迭代聚类(Simple Linear Iterative Clustering,SLIC)、能量驱动采样(Super-pixels Extracted via Energy-Driven Sampling,SEEDS)和线性谱聚类(Linear Spectral Clustering,LSC)。SLIC超像素算法是对上节讨论的k均值算法的一种改进,通常使用(但不限于)包含三个颜色分量和两个空间坐标的五维向量。
OpenCV 在 ximgproc 模块提供了ximgproc.createSuperpixelSLIC函数实现SLIC算法。需要编译opencv_contrib模块,可以参考**VS2019编译Opencv4.6.0GPU版本**,记得勾选ximgproc。
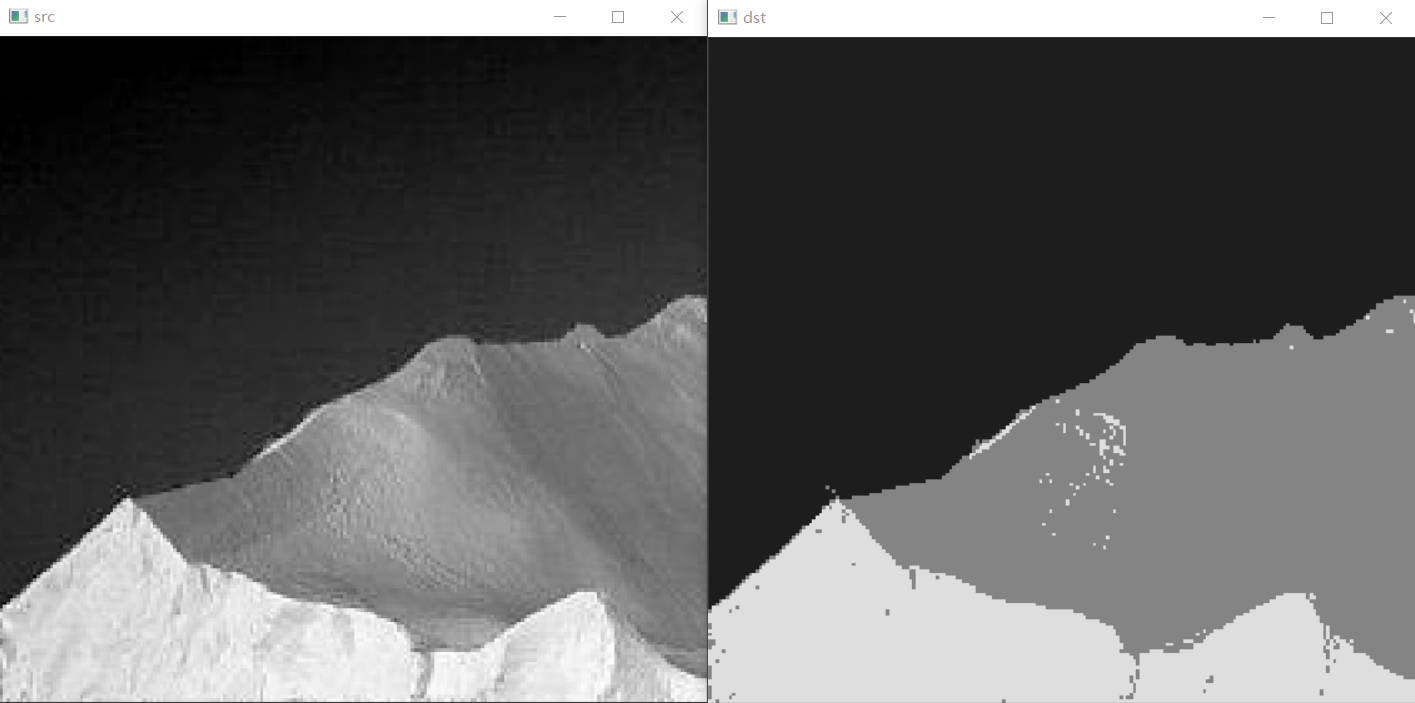
示例 SLIC超像素区域分割
| 1234567891011 | #include``using namespace ximgproc;``...``Mat src = imread(``"./14.tif"``);``Mat slicLabel, slicMask, slicColor, slicDst;``Ptr slic = createSuperpixelLSC(src);``slic->iterate(10);``//迭代次数``slic->getLabels(slicLabel);``//获取labels``slic->getLabelContourMask(slicMask);``//获取超像素的边界``int number = slic->getNumberOfSuperpixels();``//获取超像素的数量``src.setTo(Scalar(255, 255, 255), slicMask); |
参考
1.?冈萨雷斯《数字图像处理(第四版)》Chapter 10(所有图片可在链接中下载)