[人工智能]【超分辨率】（DRN）Closed-loop Matters: Dual Regression Networks for Single Image Super-Resolution

论文名称：Closed-loop Matters: Dual Regression Networks for Single Image Super-Resolution
论文下载地址：https://arxiv.org/pdf/2003.07018.pdf
论文代码地址：https://github.com/guoyongcs/DRN
但是代码有问题

论文标题：

1.论文概述

• 深度神经网络通过学习从低分辨率（LR）图像到高分辨率（HR）图像的非线性映射，已经在图像SR领域展现出良好的性能。但是现有的SR方法却存在两个潜在的缺陷：
  1. 学习从低分辨率图像到高分辨率图像的非线性映射是一个典型的ill-posed problem（我在去模糊2那篇文章里介绍了这个概念）。因此，很难寻找到一个好的解决方案。
  2. 在现实应用中，成对的LR-HR数据可能并不一定可以获得（现有的SR方法大多是采用成对LR-HR数据进行训练）并且潜在的退化模型经常是未知的。这造成了模型的自适应能力差，并不适合实际应用。
• 为了解决上面的问题，作者提出了一个对偶回归方案，通过在LR数据上引入额外的约束来减少可能的映射（函数）空间。具体而言，除了学习从LR图像到HR图像的映射，该方案还要学习一个额外的对偶回归映射来评估降采样核和重建LR图像。这就形成了一个闭环，提供了额外的监督。
• 在配对的训练数据和未配对的现实数据的SR任务上的大量实验证明了我们的方法比现有方法更加优越。

2.论文提出的背景

• 深度神经网络已经在现实应用中发挥作用，而图像超分辨率就是其中的一种应用。图像超分辨率方法将目标集中于学习从低分辨率图像到高分辨率图像之间的非线性映射来重建高分辨率图像。许多基于深度神经网络的方法被提出以改善SR的性能。但是大多数方法都有以下两个局限性：

  1. 学习从低分辨率图像到高分辨率图像之间的映射是一种典型的ill-posed problem。这是因为存在无限多个HR图像，它们可以通过下采样来获得相同的LR图像。也就是说，可能存在的将LR图像映射到HR图像的映射空间非常大，这就造成了学习性能有限。因此，怎样来减少可能的映射空间来改善SR方法的性能成为了问题的关键。
  2. 当不能获得成对的LR-HR数据时，SR方法的性能会下降。这是因为大多数SR方法的训练都依赖成对的数据，然而在真实世界里往往无法获得成对的数据，并且此外，真实世界的数据并不一定与通过特定的退化方法(如Bicubic)获得的LR图像具有相同的分布。因此，如何有效地利用未成对数据使SR模型适应于实际应用成为一个迫切而重要的问题。

• 在这篇论文中，作者提出了一种新颖的对偶回归方案来形成一个闭环结构以增强SR性能。

  1. 为了解决第一个局限，作者引入了一个额外的约束来减少可能的映射空间，这个约束是通过高分辨率图像来重建输入LR图像：在观念上，如果我们得到的从LR到HR的映射是最优的，那么将所生成的高分辨率图像下采样也应该能获得相同的输入图像。通过这样一条约束，我们可以去评估潜在的下采样核并因此减少可能的映射空间来得到一个好的由LR到HR的映射。
  2. 为了解决第二个局限，因为作者提出的对偶回归方案能够直接从LR图像进行学习，所以很容易让SR方法适应到现实数据中。

3.论文中提出的方法

3.1 用于成对数据的对偶回归方案

??现有的方法仅仅集中于学习从LR图像到HR图像的映射。但是，可能存在的映射空间非常大，这造成了训练非常困难。为了解决这个问题，作者提出了对偶回归方案。具体而言，除了学习从LR到HR的映射，我们还要学习从HR到LR的相反映射。 让$\mathrm{x}\in \mathcal{X}$为LR图像，$\mathrm{y}\in \mathcal{Y}$为HR图像。我们同时学习原始映射$P$来重建HR图像以及对偶映射$D$来重建LR图像。对偶映射可以视为对降采样核的评估。我们将SR问题转化为对偶回归方案，这涉及两个回归任务：

1. 定义一（原始回归任务）： 我们寻找一个函数$P$：$\mathcal{X}\to \mathcal{Y}$，使得预测$P(x)$与它对应的HR图像y尽可能相似。
2. 定义二（对偶回归任务）： 我们寻找一个函数$D:$ $\mathcal{Y}\to \mathcal{X}$，使得预测$D(y)$和原始输入LR图像x尽可能相似。

原始和对偶回归任务可以形成一个闭环结构并对训练模型$P$和$D$提供信息监督。如果$P(x)$是正确的HR图像，那么对偶回归预测的降采样图像$D(P(x))$应该尽可能的接近输入LR图像x。在这种约束情况下，我们可以减少可能的映射空间并使得模型更容易学习更好的映射来重建HR图像。

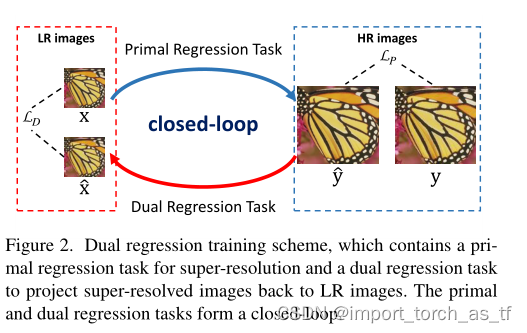
??通过结合学习这两个回归任务，作者提出的训练模型的方法如下：给定$N$对样本 S P = { ( x i , y i ) } i = 1 N \mathcal{S}_{P}=\left\{\left(\mathbf{x}_{i}, \mathbf{y}_{i}\right)\right\}_{i=1}^{N} SP?={(xi?,yi?)}i=1N?，其中$x_i$和$y_i$表示第$i$对低分辨率图像和高分辨率图像。训练损失定义如下：
$$\sum _{i=1}^N\underset{\text{primal?regression?loss?}}{{\mathcal{L}}_P\left(P\left({\mathbf{x}}_i\right),{\mathbf{y}}_i\right)}+\lambda \underset{\text{dual?regression?loss?}}{{\mathcal{L}}_D\left(D\left(P\left({\mathbf{x}}_i\right)\right),{\mathbf{x}}_i\right)}(2)$$
在这里$\lambda$控制对偶回归损失的权重。经过消融实验对比，当$\lambda$=0.1时产生了最好的结果。

3.2 用于不成对数据的对偶回归

??在现实世界里，更为普遍的SR案例是没有与之对应的HR数据的，并且LR图像的退化模型通常也未知。这样的案例使得现有的SR方法经常导致严重的自适应问题。为了减轻这个问题，作者提出了算法一来使SR方法适应新的LR数据。训练算法如下图所示：

??对偶回归映射学习潜在的退化方法，并不一定依赖于HR图像。因此我们可以使用它直接学习真实世界里未成对的LR数据来解决模型自适应问题。为了确保HR图像的重建性能，我们也引入了成对合成的数据。使用所提出的对偶回归方案，我们能够使SR方法适应各种各样不成对的数据，同时保留很好的重建性能。具体而言，给定$M$个未成对的LR样本和$N$个成对的LR-HR样本，目标损失函数定义为：
$$\sum _{i=1}^{M+N}{1}_{{\mathcal{S}}_P}\left({\mathbf{x}}_i\right){\mathcal{L}}_P\left(P\left({\mathbf{x}}_i\right),{\mathbf{y}}_i\right)+\lambda {\mathcal{L}}_D\left(D\left(P\left({\mathbf{x}}_i\right)\right),{\mathbf{x}}_i\right)(2)$$
在这里，当${\mathbf{x}}_i\in {\mathcal{S}}_P$时，$1_{{\mathcal{S}}_P}\left({\mathbf{x}}_i\right)$等于1，否则等于0。

3.3 训练方法

训练成对数据： 当给定了成对数据后，按照常见的有监督SR方法来训练模型，并最小化损失函数等式1。
训练不成对数据： 如算法1中所示，每一次迭代时先采样m个不成对数据和n个成对数据。然后端到端的训练模型，并最小化损失函数等式2。为了收敛，我们将不成对数据的数据率为$\rho$：
$$\rho =m/(m+n)(3)$$
根据论文总的消融实验证明，当$\rho$=30%时获得了最好的结果。