著名的VJ人脸检测算法就是一种基于Adaboost分类器的方法。该检测器由Paul Viola和Michael Jones在2001年的 Robust Real-Time Face Detection 提出。在当年的硬件条件下VJ算法可以达到每秒15帧图像的处理速度,是人脸检测技术发展的一个里程碑。虽然性能跟现在基于深度学习的方法没法比,但肯定也是值得去拜读的。
VJ算法利用积分图加速法快速提取图像的类Harr特征,然后使用Adaboost算法训练得到若干个强分类器,组成级联结构,对人脸和背景进行最后的分类。论文的三大贡献分别为:积分图加速法提取类Harr特征,基于Adaboost的学习算法,使用级联的方式组合强分类器。我们分开叙述。
1. 积分图加速法提取类Harr特征
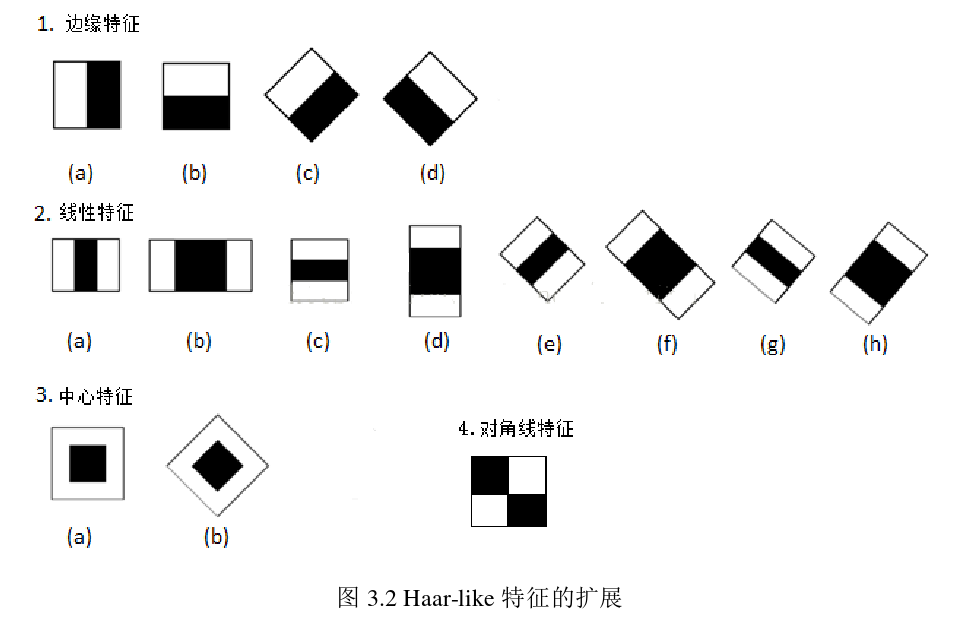

类Harr特征属于一种卷积运算模板,可以用其捕捉图像的边缘、变化等信息。而人脸的五官有着和轮廓有着独特的亮度和边缘信息,很符合类Harr特征的特点。在众多的类Harr特征模板中,Viola和Jones选取了四个可以提取边缘特征,线性特征以及对角线特征的模板。
类Harr特征值由以下操作得到:将类Harr特征模板放在图像上之后,用白色区域所覆盖的图像像素和减去黑色区域所覆盖图像中的像素和,在线性特征模板中,会对黑色区域像素之和乘以2,这是为了抵消黑白区域面积不相等所带来的影响。通过改变类Haar特征模板的位置及大小,可以在检测窗内穷举出上万个特征**,因此计算量巨大。

??由类Harr特征值的计算过程可以看出,其中涉及了大量的像素求和运算,为了更快地提取图像的类Harr特征,作者使用了一种称为积分图(Integral Image)的方法。假设有一张图像,其坐标(x, y)处的积分图可以定义为:
I
(
x
,
y
)
=
∑
x
′
≤
x
∑
y
′
≤
y
f
(
x
′
,
y
′
)
I(x, y) = \sum_{x^{\prime} \leq x} \sum_{y^{\prime} \leq y} f\left(x^{\prime}, y^{\prime}\right)
I(x,y)=∑x′≤x?∑y′≤y?f(x′,y′)
在提取类Harr特征之前,首先计算出整幅图像的积分图。那么在提取特征时,图中矩形ABCD的像素和可以利用积分图表示如下:
S
a
b
c
d
=
I
(
D
)
?
I
(
B
)
?
I
(
C
)
+
I
(
A
)
S_{a b c d}=I(D)-I(B)-I(C)+I(A)
Sabcd?=I(D)?I(B)?I(C)+I(A)
积分图加速法大大降低了运算量。
2. Adaboost学习算法
提到了大量类Harr特征值之后,就该使用Adaboost算法做分类训练了
关于Adaboost的好文推荐:详解AdaBoost原理, 这里我只记录关键点吧。
Boosting是一种将弱分类器组合起来形成强分类器的算法框架。这种“三个臭皮匠顶个诸葛亮”的思路是有理论基础的。
Boosting 体现了提升思想,每一个弱学习器重点关注前一个训练器不足的地方进行训练,通过加权投票的方式,得出预测结果。Boosting学习是串行的,弱学习器的学习有先后顺序。
而Adaboost是其中的一种,采用了exponential loss function(其实就是用指数的权重),根据不同的loss function还可以有其他算法,比如L2Boosting, logitboost。
2.1 Boosting
Boosting其架构如下图:
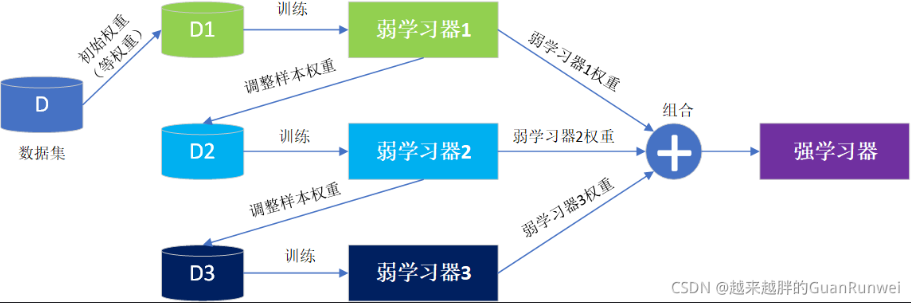
在Boosting的迭代式训练时,每个训练样本的初始权值是相同的,训练中根据弱学习器的误差计算弱学习器的权重,并调整样本的权重来改变样本的分布,使先前弱学习器难分的样本在后续训练中得到更大的关注,循环该过程,直到弱学习器的数目达到指定数量(是一个超参)。最终将所有弱学习器进行组合加权,得到集成的强学习器。
弱分类器:
一个检测窗中包含大量的类Harr特征,对于检测窗x中的第j个特征值,可以训
练一个如下式所示的弱分类器:
h
j
(
x
)
=
{
1
?如果?
p
j
f
j
(
x
)
<
p
j
θ
j
0
?其他?
h_{j}(x)=\left\{\begin{array}{ll} 1 & \text { 如果 } p_{j} f_{j}(x)<p_{j} \theta_{j} \\ 0 & \text { 其他 } \end{array}\right.
hj?(x)={10??如果?pj?fj?(x)<pj?θj??其他??
其中
f
j
(
x
)
f_{j}(x)
fj?(x)表示检测窗第j个特征值,
θ
\theta
θ表示阈值,p表示不等号方向,训弱分类器就是在当前特定样本分布下,确定
f
j
(
x
)
f_{j}(x)
fj?(x)的一个阈值,使
h
j
(
x
)
h_{j}(x)
hj?(x)的分类错误率降到最低。
2.2 Adaboost(Adaptive Boosting)的算法过程
-
初始化训练样本的权值分布 D 1 D_{1} D1?。假设有N个训练样本数据,则每一个训练样本最开始时,都会被赋予相同的权值: W 1 = 1 / N W_{1} = 1/N W1?=1/N。
-
(a) 选取一个当前误差率最低的弱分类器 h 作为第 t 个基本分类器 H t H_{t} Ht? , 并 计算弱分类器 h t : X → { ? 1 , 1 } h_{t}: X \rightarrow\{-1,1\} ht?:X→{?1,1}, 该弱分类器在分布 D t D_{t} Dt? 上的误差为:
e t = P ( H t ( x i ) ≠ y i ) = ∑ i = 1 N w t i I ( H t ( x i ) ≠ y i ) e_{t}=P\left(H_{t}\left(x_{i}\right) \neq y_{i}\right)=\sum_{i=1}^{N} w_{t i} I\left(H_{t}\left(x_{i}\right) \neq y_{i}\right) et?=P(Ht?(xi?)=yi?)=∑i=1N?wti?I(Ht?(xi?)=yi?)那么由上述式子可知, H f ( x ) H_{\mathrm{f}}(x) Hf?(x) 在训练数据集上的误差率 e w e_{\mathrm{w}} ew? 就是被 H r ( x ) H_{\mathrm{r}}(x) Hr?(x) 误分类 样本的权值之和。
(b) 更新每个弱分类器在最终分类器中的权重 (弱分类器权重用 α \alpha α 表示):
α t = 1 2 ln ? ( 1 ? e t e t ) \alpha_{t}=\frac{1}{2} \ln \left(\frac{1-e_{t}}{e_{t}}\right) αt?=21?ln(et?1?et??)
显然,误差越小,权重越大,这是一种指数更新弱分类器权值的形式。
(c) 更新训练样本的权值分布 D r + 1 D_{\mathrm{r}+1} Dr+1? :
D t + 1 ( x ) = D t ( x ) Z t × { exp ? ( ? α t ) , ?if? h t ( x ) = f ( x ) exp ? ( α t ) , ?if? h t ( x ) ≠ f ( x ) = D t ( x ) exp ? ( ? α t f ( x ) h t ( x ) ) Z t \begin{array}{l} \mathcal{D}_{t+1}(\boldsymbol{x})=\frac{\mathcal{D}_{t}(\boldsymbol{x})}{Z_{t}} \times\left\{\begin{array}{ll} \exp \left(-\alpha_{t}\right), & \text { if } h_{t}(\boldsymbol{x})=f(\boldsymbol{x}) \\ \exp \left(\alpha_{t}\right), & \text { if } h_{t}(\boldsymbol{x}) \neq f(\boldsymbol{x}) \end{array}\right.\\ =\frac{\mathcal{D}_{t}(\boldsymbol{x}) \exp \left(-\alpha_{t} f(\boldsymbol{x}) h_{t}(\boldsymbol{x})\right)}{Z_{t}} \end{array} Dt+1?(x)=Zt?Dt?(x)?×{exp(?αt?),exp(αt?),??if?ht?(x)=f(x)?if?ht?(x)=f(x)?=Zt?Dt?(x)exp(?αt?f(x)ht?(x))??
其中 α t \alpha_{t} αt? 为弱分类器的权重, Z t Z_{t} Zt? 为归一化常数 ,以确保D是一个分布, Z t = 2 e t ( 1 ? e t ) Z_{t}=2 \sqrt{e_{t}\left(1-e_{t}\right)} Zt?=2et?(1?et?)?
可以看出,训练样本权值的更新仍然是使用指数函数的形式,因为相比0-1损失函数指数函数有更好的数学性质。 -
最后, 按弱分类器权重 α t \alpha_{t} αt? 组合各个弱分类器, 即
f ( x ) = ∑ i = 1 T α i H t ( x ) f(x)=\sum_{i=1}^{T} \alpha_{i} H_{t}(x) f(x)=∑i=1T?αi?Ht?(x)通过符号函数 sign ? \operatorname{sign} sign 的作用, 得到一个强分类器为:
H f i n a l = sig ? n ( f ( x ) ) = sign ? ( ∑ t = 1 T α t H t ( x ) ) H_{f i n a l}=\operatorname{sig} n(f(x))=\operatorname{sign}\left(\sum_{t=1}^{T} \alpha_{t} H_{t}(x)\right) Hfinal?=sign(f(x))=sign(∑t=1T?αt?Ht?(x))
第二步中的训练样本权重更新源头是基于误差率e的,所以可以推导出直接使用e更新训练样本权值的公式:
错误分类样本, 权值更新 :
D
t
+
1
(
x
)
=
D
t
(
x
)
2
e
t
D_{t+1}(x)=\frac{D_{t}(x)}{2 e_{t}}
Dt+1?(x)=2et?Dt?(x)?
正确分类样本, 权值更新 :
D
t
+
1
(
x
)
=
D
t
(
x
)
2
(
1
?
e
t
)
D_{t+1}(x)=\frac{D_{t}(x)}{2\left(1-e_{t}\right)}
Dt+1?(x)=2(1?et?)Dt?(x)?
3. 强分类器的级联
在VJ人脸检测器中,最终的分类器是由若干个Adaboost强分类器级联而成。在级联结构中排在前面的强分类器由一些最能够代表人脸特征的少量弱分类器组成,这样可快速过滤掉大部分非面部区域,排在后面的强分类器构造越来越复杂,对检测子窗口要求越来越严格,用来判断较难辩识的区域。
VJ人脸检测器中强分类器组成的联结构示意图:
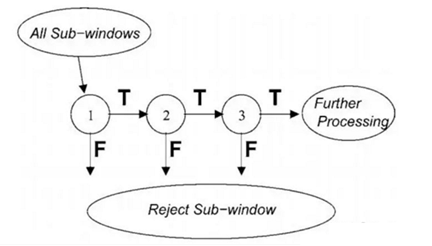
现在看VJ的性能是很差的,但该工作是里程碑式的,这里记录一下。