[人工智能]每天五分钟机器学习算法：拉格朗日乘数法和KKT条件

KKT条件

当我们要求一个函数的极值，同时还有两种类型的约束条件，一种约束条件是等式约束，另外一种约束是不等式约束：

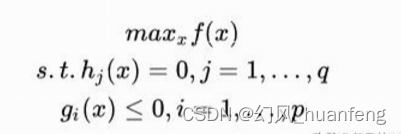
x是一个变量（n维，n个样本），我们想要找到使得f(x)最大的x，还要满足上面的约束。此时KKT条件就出来说话了，如果要想让x满足这个条件下的f(x)的最大值（极值点），那么需要满足KKT条件，条件如下：

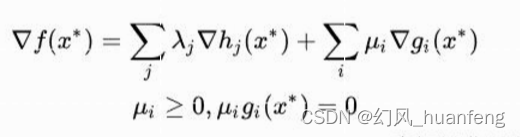
我们来解释一下这个KKT条件，在极值点处f的梯度是一系列的不等式gi(x*)和等式hj(x*)的线性组合，其中不等式的约束ui≥0，而等式的λi不做约束，gi(x*)有＜0，和=0两种情况，但是如何＜0，那么μi一定是0（其实此时对应的xi就是非支持向量），也就是说只有gi(x*)=0的时候，此时ui才不是0（此时对应的xi就是支持向量），换句话说，只有x*在边界gi(x*)=0的时候，此时的gi才会出现在加权式中，接下来我们可以看到，也就是说支持向量才会起作用。

拉格朗日乘数法

我们在高等数学中经常会需要求解

了解本专栏 订阅专栏 解锁全文