? ? ? ? 这一节主要介绍一下基于单张图的图像超分算法。图像超分,就是要从低分辨率的图像恢复为高分辨率的图像,它在日常的图像和视频存储与浏览中都有广泛的应用。
基于深度学习的图像超分算法
不同的采样结构
????????图像超分需要将低分辨率图片恢复为高分辨率图像,因此上采样结构在网络中是必不可少的,因此下面按照上采样结构在不同CNN模型中的位置来区分不同的算法,说明一下其原理和优缺点。
前上采样
????????前上采样即在网络的开始完成上采样过程,经典模型为SRCNN模型,其结构如下:
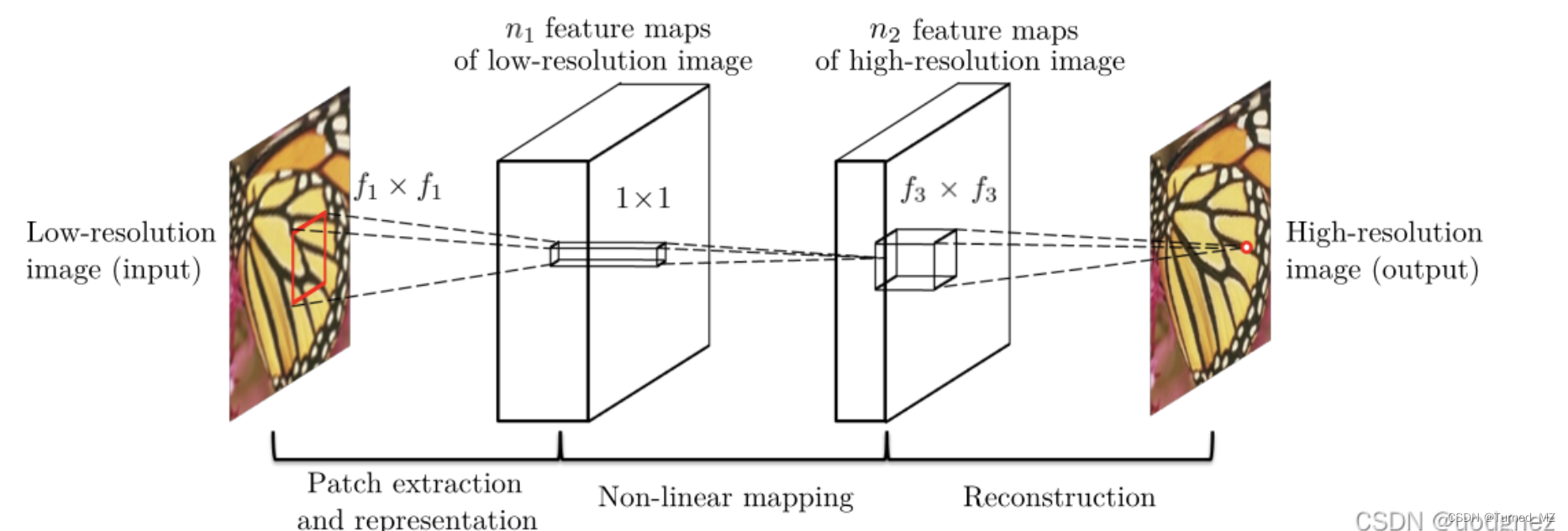
SRCNN模型步骤:
- 首先使用双线性插值等上采样方法进行初始化,得到目标分辨率大小的图像。
- 使用卷积层对输入的局部图像块进行特征提取,得到一系列特征图,即f1
- 接着使用1x1卷积进行维度变换,即扩增特征通道数
- 最后将高分辨率的图像块重新拼接为完成的图像,即f3
该模型学习过程比较简单,但是由于整个网络在高分辨率空间进行计算,因此计算量大,而且噪声容易被放大。
后上采样
后上采样即在网络的后部分才进行上采样。比较经典的模型结构为FSRCNN和ESPCN。
FSRCNN网络结构如下:
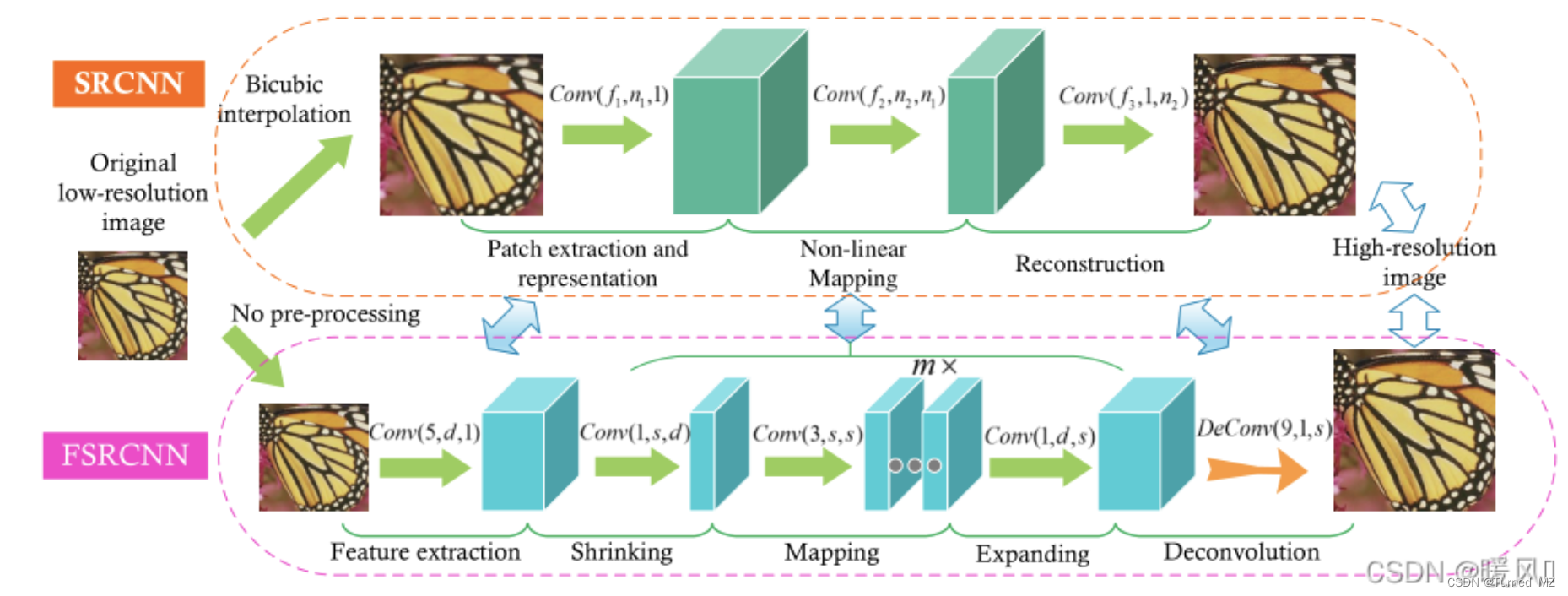
想比SRCNN,主要改进在三个地方:
- FSRCNN采用原始低分辨率图像作为输入,无需进行双三次插值,在网络末端引入反卷积层来完成上采样,极大的减小了网络参数。
- 网将SRCNN中的非线性映射层替换为FSRCNN中的三个层,即收缩、映射和扩展,减少特征参数维度。
- 将“宽”的非线性映射层用“**窄”的“深”**的网络来替代。
ESPCN网络结构如下:
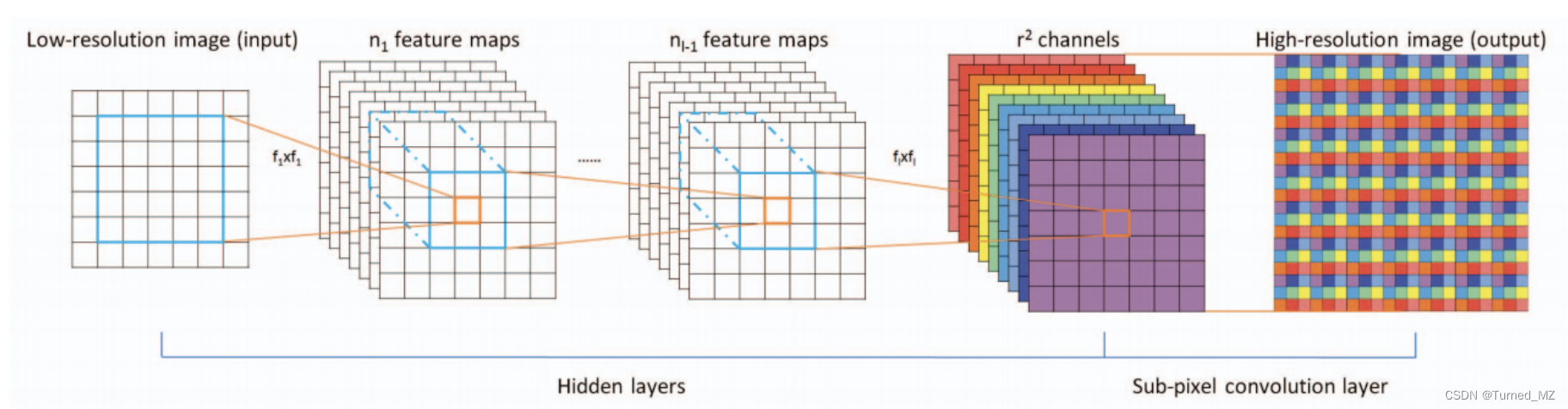
????????该网络的关键亮点在于亚像素卷积层,首先介绍一下亚像素的概念:
????????面阵摄像机的成像面以像素为最小单位。在相机成像的过程中,获得的图像数据是将图像进行了离散化处理。例如两个感官元件上的像素之间有4.5um的间距,宏观上它们是连在一起的,微观上它们之间还有无数更小的东西存在,这个更小的东西就称之为“亚像素”。实际上,亚像素应该是存在的,只是缺少更细微的传感器把它检测出来,只能通过软件将起近似计算出来。
????????如下图所示,每四个红色点围成的矩形区域为实际原件上的像素点,黑色点为亚像素点:
????????根据相邻两像素之间插值情况的不同,可以调整亚像素的精度,例如四分之一,就是将每个像素从横向和纵向上当做四个像素点。也就是上面图里的红色点之间有三个黑色点。这样通过亚像素插值的方法可以实现从小矩形到大矩形的映射,从而提高分辨率。
????????在原文中,作者将网络模型定义为3层,前两层为普通卷积,最后的亚像素卷积层则包括两个部分,卷积+像素排列。即通过三个卷积层,得到与输入图像尺寸一致、通道数为r2的特征图像,再将特征图像的每个像素的r2个通道重新排列成一个r * r的区域,对应高分辨图像中一个r * r的区域,从而大小为H*W*r2的特征图像重新排列为rH*rW*1的高分辨率图像。
?逐步式上采样
为了解决后采样模型无法对高倍率因子进行很好的超分的问题,逐步式上采样被提出,比较典型的为LapSRN,其网络结构为:
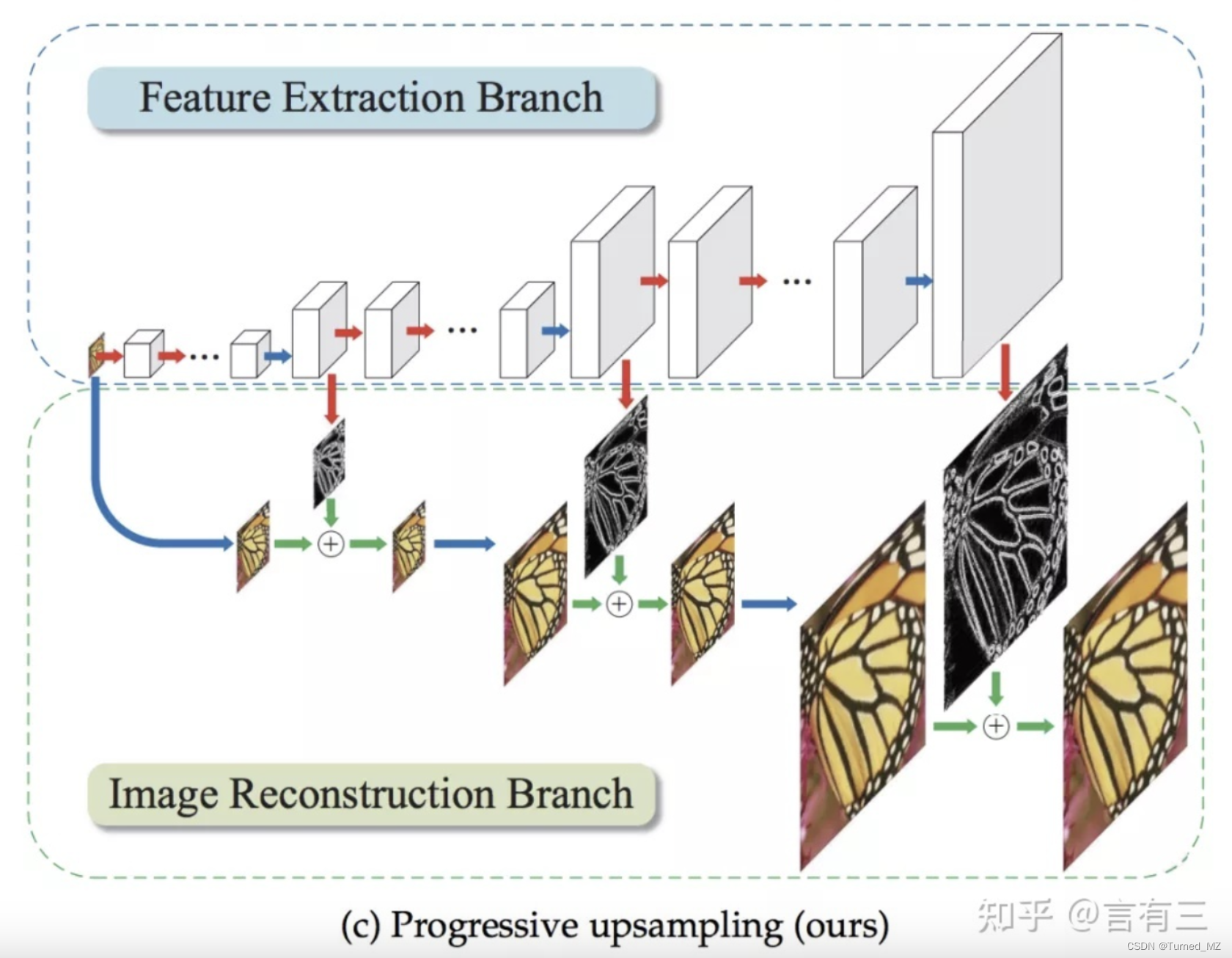
????????其主要包含两个分支:特征提取分支(即上图中上半部分)和图像重建分支(即图像中下半部分),其中特征提取分支包含多个不同分辨率层级,每一个层级使用多个卷积层来获取非线性特征映射,最后加上反卷积层来提升图像的分辨率;图像重建分支则将输入图进行上采样后和相同分辨率大小的特征提取分支相加来得到下一级分辨率的输出图,直到得到最终的高分辨率结果图。?
优化目标
????????早期的基于CNN模型的超分框架如SRCNN,ESPCN都使用图像像素空间的欧式距离(即L2 loss,或者MSE损失)作为优化目标,结果能取得较高的PSNR和SSIM指标,但是存在结果过于平滑的问题。
????????人眼对重建结果质量的感知并不完全与这些指标相符,比如MSE指标较小并不能保证局部细节的清晰度,而较大的MSE指标也并不等价于较差的结果,比如原图偏移一个像素后与原图的MSE值可能较大,但是视觉感知效果很接近。
????????CNN网络的高层特征空间相比于原始的像素空间,具有较高的抽象层级,它使得原始图像的特征与目标图像的特征差异可以反应在语义级别,这非常符合人眼的主观评估感受,研究者基于此提出了感知损失。基于特征空间计算的欧式距离被称为感知损失(perceptual loss),令φ来表示网络,j表示网络的第j层,表示第j层的特征图的大小,感知损失的定义如下;

