开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 【计算机视觉】哈里斯角点检测 Harris Corner Detection -> 正文阅读

[人工智能]【计算机视觉】哈里斯角点检测 Harris Corner Detection

欲速则不达，哈里斯角点检测是一个不简单也不复杂的概念方法，但是需要了解很多前置概念，一步步来。但是想要一步到位，也可以直接跳过第一部分的前置概念理解部分。

前置概念

数字图像概念

什么是数字图像概念？
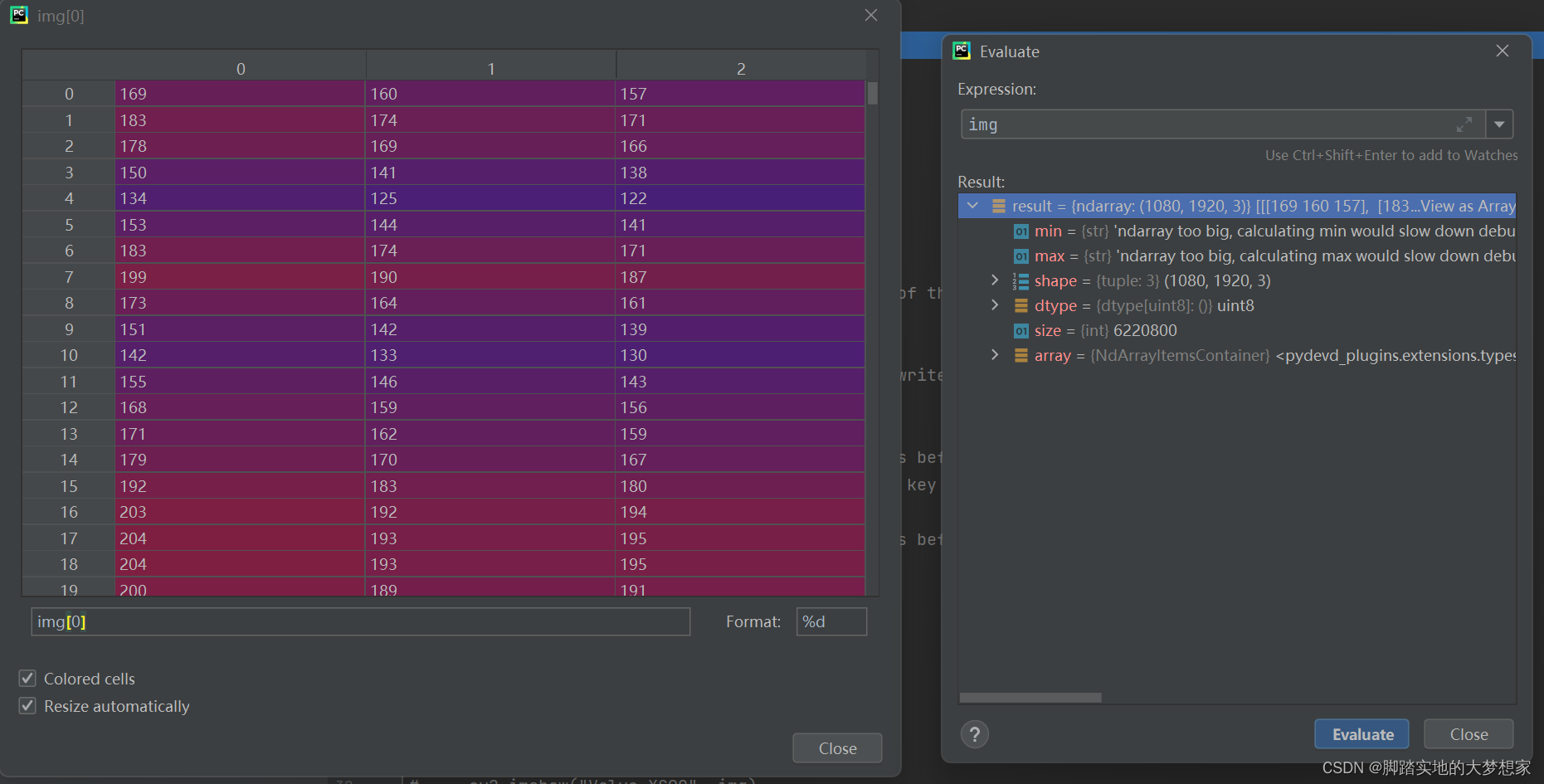
这是我最喜欢的SUV，沃尔沃XC90，在我们眼中，我们都看出这是一个非常漂亮的汽车的图片，但是在计算机的识别后，是什么？

在这里插入图片描述

在计算机图像中，该图像是一个数组，其中包含元素数量为 192010803，其中3为三层通道Channel；而通过对图像属性的对比，发现图像的分辨率也为1920*1080。说明经过数字化处理，图像的每个像素在计算机中都被转化为一个值。

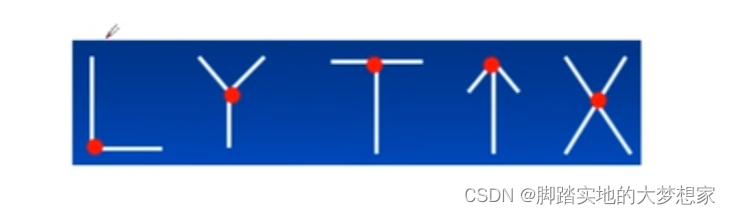
在这里插入图片描述

角点

什么是角点？
在这里插入图片描述
角点说白了就是物体边缘的拐点。通过对角点的识别，我们可以实现很多功能，比如：
实现图片的拼接：

三维重建：

等等…

哈里斯角点原理

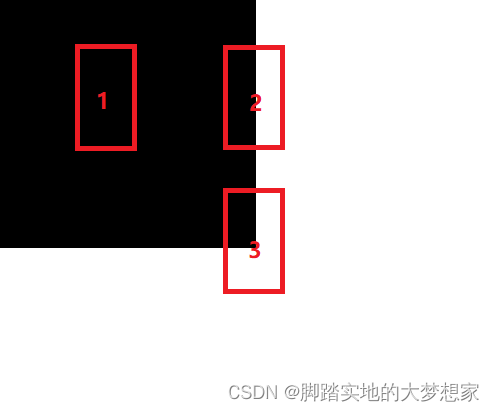
通过对比下述三张图，理解哈里斯对于角点的定义。

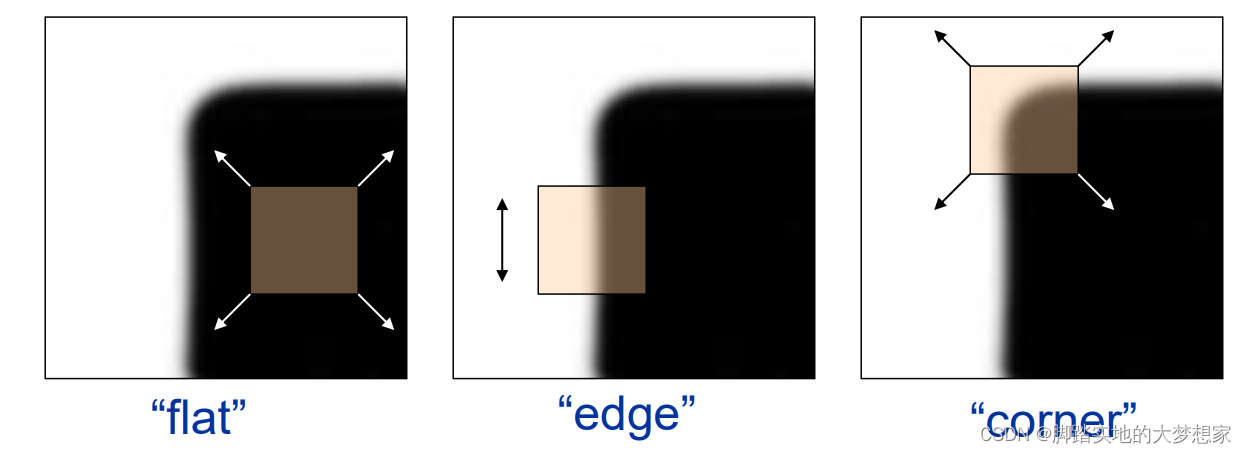
在这里插入图片描述
首先，我们选择一个合适大小的像素框，如途中金黄色区域。我们试图通过对框中像素值的变化去探究是否为角点。
第一个 flat，我们在上下左右以及对角线移动像素框时，会发现框中的值几乎没有变化，全部为黑色值0；
第二个 edge，我们在上下移动时，发现像素框中值没有变化，但是左右移动时以及对角线移动时会发生变化；
第三个 corner，我们不论上下移动还是左右移动还是对角线移动，都会发生变化，所以其为角点。

将上述哈里斯角点原理化为公式来看：
$E(u,v)=\sum _{x,y}w(x,y) [I(x+u,y+v)-I(x,y)]^2$
其中， $u, v$ 分别代表着在竖直和水平方向上的偏移， $w (x, y)$ 为像素框的中心； $I (x + u, y + v)$ 为像素框位移之后坐标加偏移 $(x + u, y + v)$ 的灰度值， $I (x, y)$ 为位移之前坐标位置 $(x, y)$ 的灰度值。

其结果：E代表的就是 “平移前选定的红框中每个像素” 与 “平移后选定的绿框的每个像素” 对应位置的差的平方和。

在这里插入图片描述

泰勒展开

泰勒展开将一些复杂的函数逼近近似的表示为简单的多项式函数。
$f(x)=f(x_0)+f'(x_0)(x-x_0)+\frac {f''(x_0)} 2(x-x_0)^2+...+\frac {f^{(n)}(x_0)} {n!}(x-x_0)^n+o[(x-x_0)^n]$

上述泰勒公式使用的余项是皮亚诺余项。

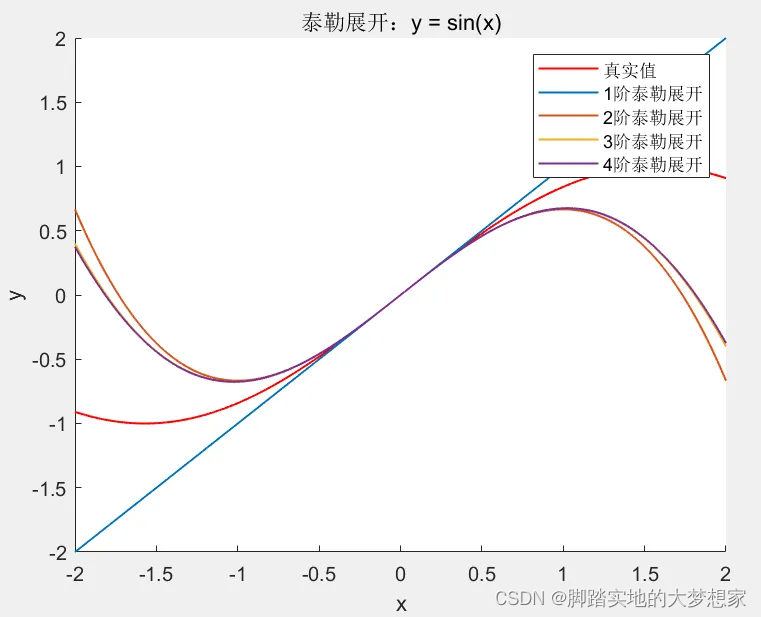
在这里插入图片描述

通过上图理解，通过不断的进行泰勒展开，不断逼近原函数曲线；我们可以通过泰勒公式来获取函数的信息。

哈里斯角点检测与泰勒公式

通过一阶泰勒公式 $f(x)=f(x_0)+f'(x_0)(x-x_0)$ ，我们可以将哈里斯角点检测灰度值函数 $I (x + u, y + v)$ 公式化为：
$I(x+u,y+v)≈I(x,y)+I_xu+I_yv$

其中
$I_xu=\frac {dI} {dx} u；I_yv=\frac {dI} {dy} v$

所以有：

$E(u,v)=\sum _{x,y} w(x,y)[I(x+u,y+v)-I(x,y)]^2$
$≈w(x,y)\sum _{x,y} [I(x,y)+I_xu+I_yv-I(x,y)]^2$
$=w(x,y)\sum _{x,y} [I_xu+I_yv]^2$
$=w(x,y)\sum _{x,y} (I_x^2u^2+2I_xI_yuv+I_y^2v^2)$

而又因为 $w (x, y)$ 代表的就是像素框中心点值，不是我们主要研究的部分，可以暂时从 $E (u, v)$ 的计算中提出来，所以可以将 $E (u, v)$ 表示为：

$E(u,v)=[u^2 \sum_{x,y} I_x^2 + 2uv\sum_{x,y} I_xI_y +v^2\sum_{x,y} I_y^2]$

转换成矩阵形式：
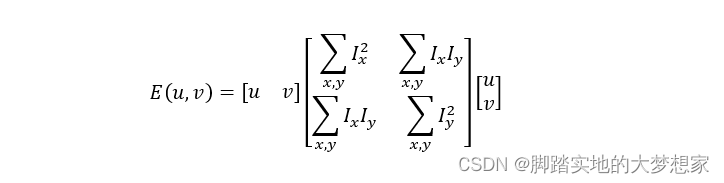
在这里插入图片描述
推导如下：

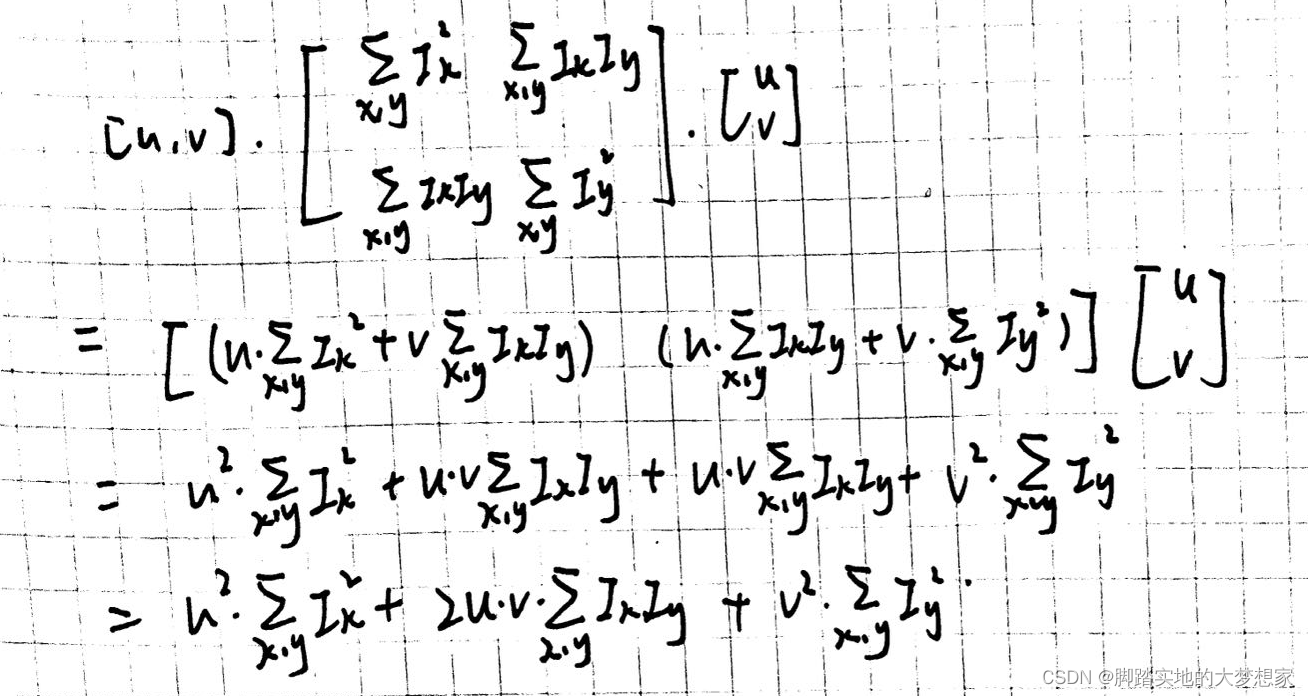
下一步，我们需要对 $I_x$ 与 $I_y$ 的意义进行探究。

探究 $I_x$ 与 $I_y$ 值的意义

首先，上述已经说明， $I_x=\frac {dI} {dx}$ ， $I_y=\frac {dI} {dy}$ ， $I (x, y)$ 代表着 $(x, y)$ 点的像素值。

其次，我们有求平移前后对应像素差平方值的函数 $E (u, v)$
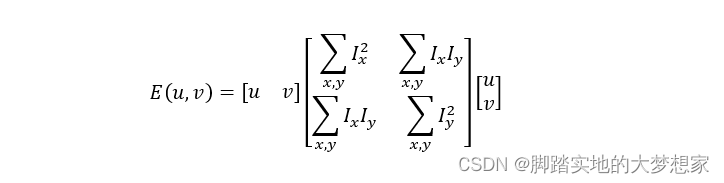
在这里插入图片描述
我们可以将该函数表示为：

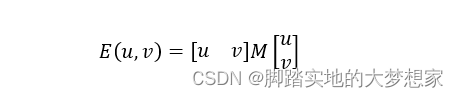
即：

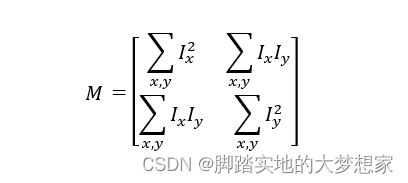
所以我们下面将对矩阵 $M$ 进行研究：

对于每一个边缘上的点而言，当 $\frac {dI} {dx}$ 有意义时， $\frac {dI} {dy}$ 值很小约为0；当 $\frac {dI} {dy}$ 有意义时， $\frac {dI} {dx}$ 值很小约为0。当然除了角点。如图所示：

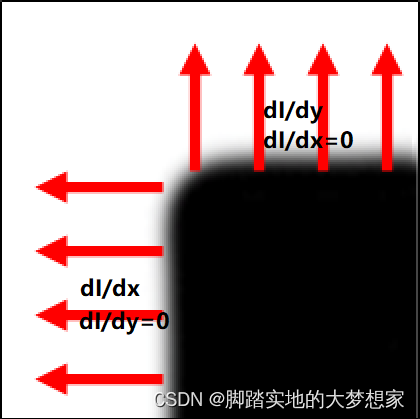
在这里插入图片描述

所以一共存在三种情况的点：

不在边界的 $\frac {dI} {dx}=\frac {dI} {dy}≈0$ 的点
在边界的 $\frac {dI} {dx}>>0，\frac {dI} {dy}≈0$ 或 $\frac {dI} {dy}>>0，\frac {dI} {dx}≈0$ 的点；
角点 $\frac {dI} {dx}>>0，\frac {dI} {dy}>>0$

如果向完全理解 $\frac {dI} {dx}$ 与 $\frac {dI} {dy}$ ，需要结合 索贝尔 (Sobel) 算子 进行理解。

索贝尔算子 Sobel

因为本节博客主要介绍哈里斯角点检测，所以这里只简单介绍一下索贝尔算子。

首先，明确索贝尔算子的作用为 边缘检测。
索贝尔有两个算子，一个是检测水平边缘；另一个是检测垂直边缘；

$e . g .$ 假设我们想要检测原始图像 $A$ 的横向边缘以及纵向边缘， $G_x$ 为横向索贝尔算子， $G_y$ 为纵向索贝尔算子。

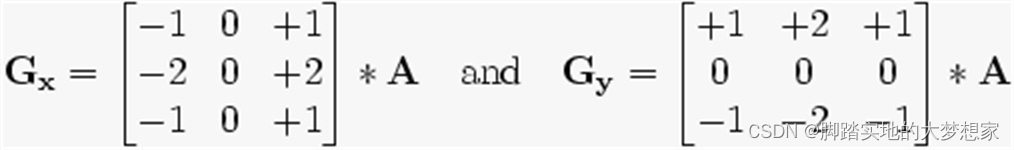
在这里插入图片描述
$e . g .$ 案例：对比下面三个原始图片的索贝尔算子结果：

代码：

# 索贝尔算子
import cv2

cv2.namedWindow('video', cv2.WINDOW_NORMAL)
cv2.resizeWindow('video', 640, 480)

img = cv2.imread("Sobel_0.png")

sobel_x = cv2.Sobel(img[:, :, 0], cv2.CV_16S, 1, 0)
sobel_y = cv2.Sobel(img[:, :, 0], cv2.CV_16S, 0, 1)

absX = cv2.convertScaleAbs(sobel_x)
absY = cv2.convertScaleAbs(sobel_y)
# # 横向边缘检测
# dst = cv2.addWeighted(absX, 1, absY, 0, 0)
# # 纵向边缘检测
# dst = cv2.addWeighted(absX, 0, absY, 1, 0)
# 横向+纵向边缘检测
dst = cv2.addWeighted(absX, 0.5, absY, 0.5, 0)
cv2.imshow("video", dst)

cv2.waitKey(0)
cv2.destroyAllWindows()

原始图片： Sobel_0.png；Sobel_1.png；Sobel_2.png
在这里插入图片描述
对三个图片分别做横向边缘检测：

对三个图片分别做纵向边缘检测：
在这里插入图片描述

对三个图片分别做横向+纵向边缘检测：
在这里插入图片描述
以上便是Sobel算子的基本实现。

回到哈里斯，结合索贝尔，继续探究 $I_x$ 与 $I_y$ ：

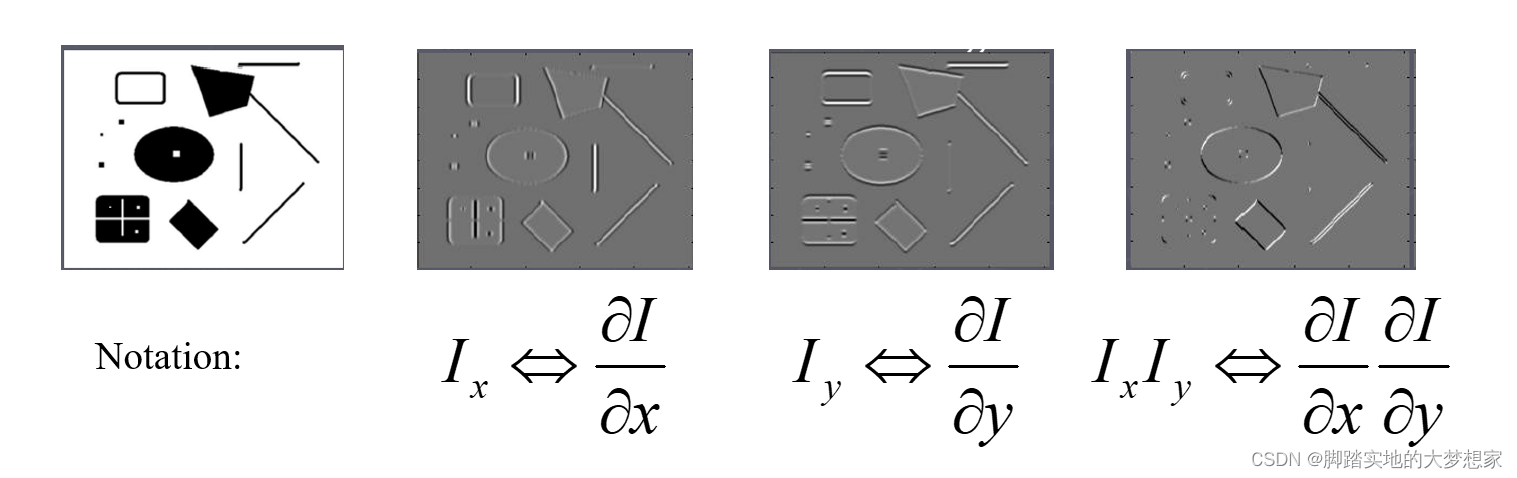
在这里插入图片描述
构建三种情况下梯度统计图与梯度图：

在这里插入图片描述
梯度统计图： $I_x$ 为水平方向的梯度值， $I_y$ 为竖直方向的梯度值。

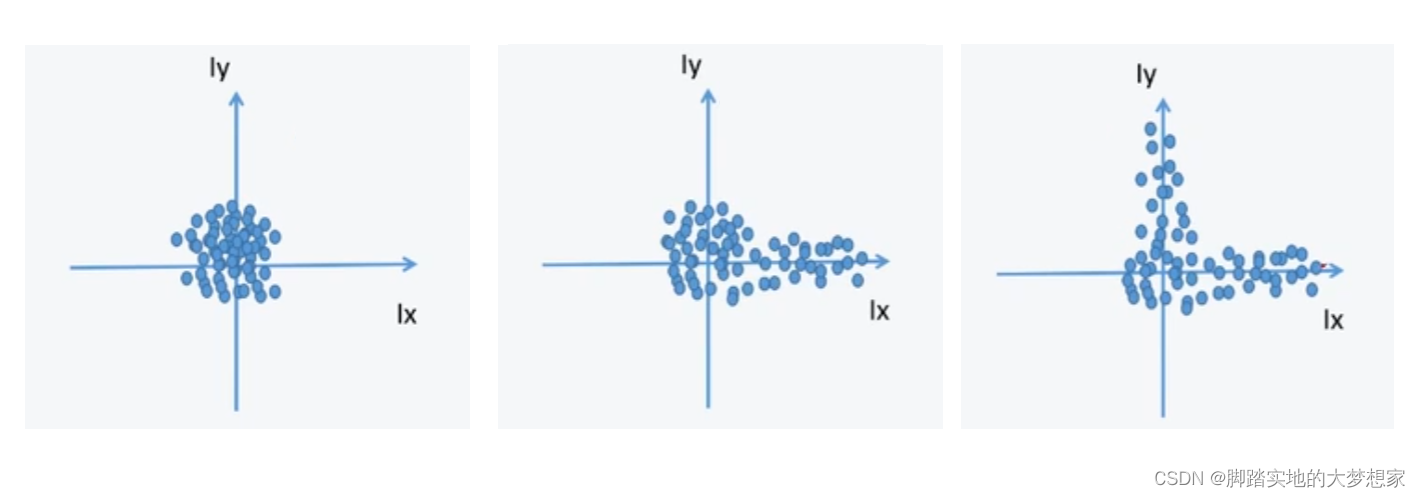
很明显，平坦点几乎没有什么梯度变化，周围没有什么像素的变化，值趋近于0；
而边缘点，只有一个方向有梯度变化，上上图中区域2的变化是在水平移动有像素值有变化，竖直方向移动，像素值几乎没有变化；
而角点，两个方向的移动都会有梯度的变化，都有像素值的大量改变。

梯度图：
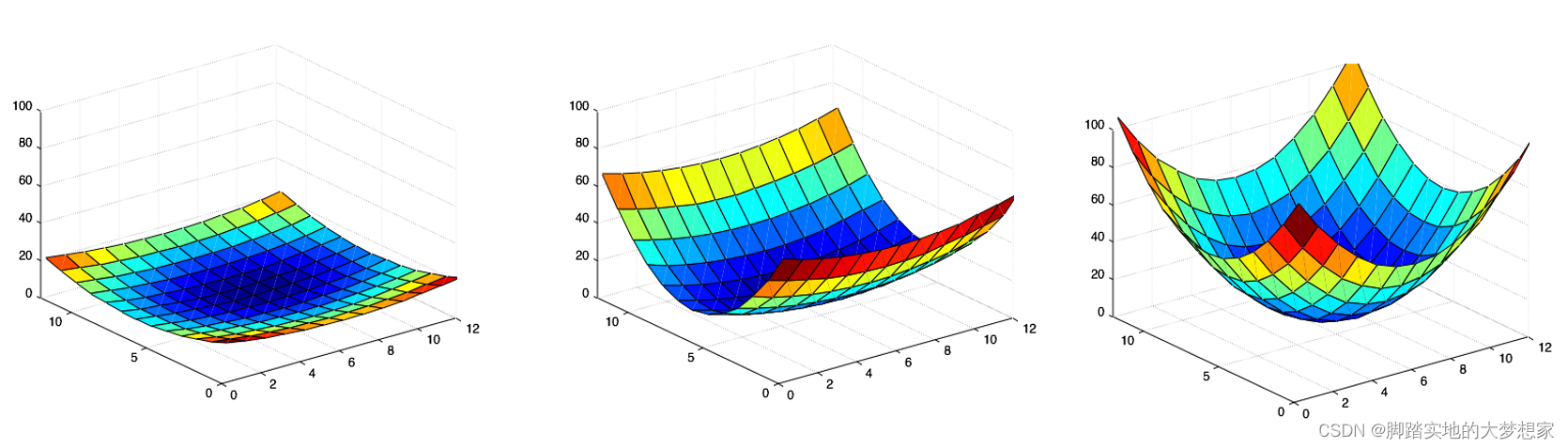
在这里插入图片描述
平坦点的移动几乎没有任何像素值的变化；
边缘点的移动会在一个方向有大量像素值的变化，而另一个方向如同平坦点一样；
角点会在两个方向都有大量像素值的变化。

通过上述加强了对：角点与边缘和平坦的理解，下面将回归公式，从对角点响应大小判定的方案去判定是否为角点。

角点响应

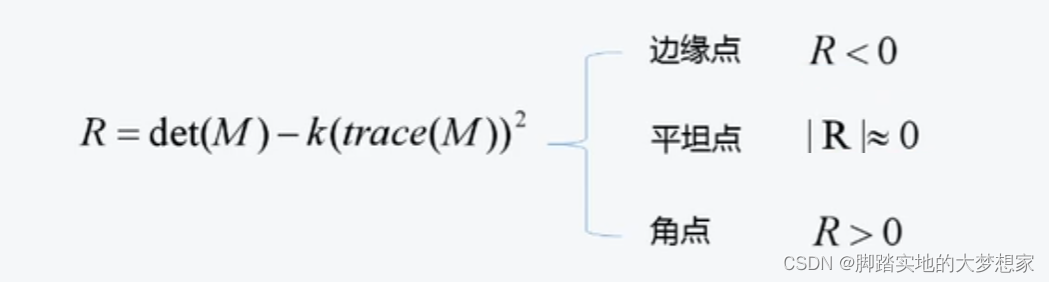
在这里插入图片描述

角点响应公式： $R=det(M)-k(trace(M))^2$
其中：
$d e t (M)$ 为求矩阵M的行列式的值， $det(M)=I_x^2*I_y^2-I_xI_y*I_xI_y$ ；
$k$ 称为经验值，一般为 $0.04$ ~ $0.06$ ；
$t r a ce (M)$ 为矩阵对角线的和， $trace(M)=I_x^2+I_y^2$

通过 $R$ 的值，来判断是角点的强度，也可以说来判断是角点的真实性。

在这里插入图片描述

前置知识到此结束，下面将通过代码案例实际进行一张图片的角点检测。

哈里斯角点检测一般流程

1、彩色图像转化为灰阶图像；
2、计算空间微分（泰勒展开）；
3、建构结构张量（Sobel算子）；
4、计算哈里斯响应（角点响应）；
5、非极大值抑制（筛选点）。

哈里斯角点检测python代码

# harris detector

import cv2
import numpy as np

'''
    image: 源图片；
    blocksize：窗口大小；
    ksize：索贝尔梯度计算的Kernel大小；
    k：角点响应R的经验值系数。
'''
def cornerHarris(image, blocksize=2, ksize=3, k=0.04):

    def _clacHarris(cov,k):
        result = np.zeros([cov.shape[0], cov.shape[1]], dtype=np.float32)
        for i in range(cov.shape[0]):
            for j in range(cov.shape[1]):
                a = cov[i, j, 0]
                b = cov[i, j, 1]
                c = cov[i, j, 2]
                result[i, j] = a * c - b * b - k * (a + c) * (a + c)

        return result

    # Sobel
    sobel_x = cv2.Sobel(image, cv2.CV_32F, 1, 0, ksize=ksize)
    sobel_y = cv2.Sobel(image, cv2.CV_32F, 0, 1, ksize=ksize)

    # 建立存储R值矩阵
    cov = np.zeros([image.shape[0], image.shape[1], 3], dtype=np.float32)

    # 计算Ix^2,Iy^2与Ix*Iy
    for i in range(image.shape[0]):
        for j in range(image.shape[1]):
            cov[i,j,0] = sobel_x[i,j] * sobel_x[i,j]
            cov[i,j,1] = sobel_x[i,j] * sobel_y[i,j]
            cov[i,j,2] = sobel_y[i,j] * sobel_y[i,j]

    # 计算梯度和
    cov = cv2.boxFilter(cov, -1, (blocksize, blocksize), normalize=False)

    return _clacHarris(cov,k)

if __name__ == '__main__':
    img = cv2.imread("harris_detector.jpg")
    # 将图片转化为灰度图
    gray_img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    # 哈里斯角点检测
    result = cornerHarris(gray_img, 2, 3, 0.04)
    # 筛选
    pos = cv2.goodFeaturesToTrack(result, 0, 0.01, 10)
    for i in range(len(pos)):
        cv2.circle(img, (int(pos[i][0][0]), int(pos[i][0][1])), 1, [255,0,0], thickness=2)
    cv2.imshow('harris',img)
    cv2.waitKey(0)