目录
1.linear programming (LP,线性规划)

不等式约束:
目标函数:仿射函数
不等式约束:仿射函数
可行域:polyhedron set(多面体集?)
solution: simplex method
2.quadratic programming (QP,二次规划)
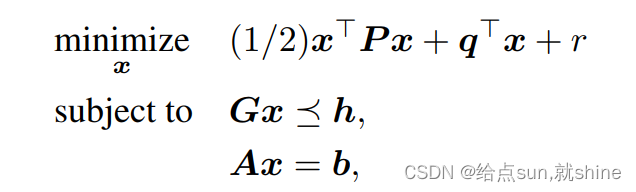
特点:
目标函数:
P
P
P需要半正定
不等式约束:仿射函数
可行域:polyhedron set(多面体集?)
3.second-order cone programming (SOCP,二阶锥规划)
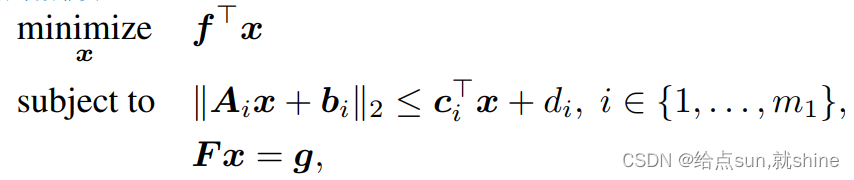
特点:
不等式约束:仿射函数的范数
≤
\leq
≤ 仿射函数
形如 ∥ A i x + b i ∥ 2 ? c i ? x ? d i ≤ 0 \left\|\boldsymbol{A}_i \boldsymbol{x}+\boldsymbol{b}_i\right\|_2-\boldsymbol{c}_i^{\top} \boldsymbol{x}-d_i \leq 0 ∥Ai?x+bi?∥2??ci??x?di?≤0的式子称为二阶锥,它形如冰淇淋状
4.Semidefinite progranmming(SDP,半定规划)
4.1 形式一
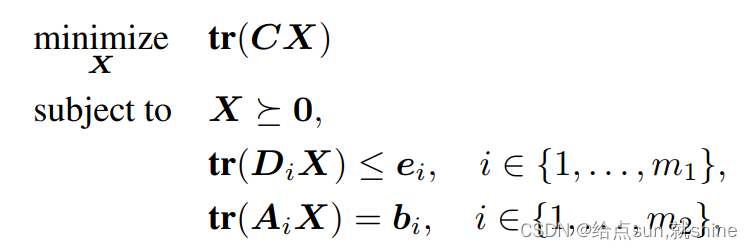
特点:
tr
?
(
?
)
\operatorname{tr}(\cdot)
tr(?)代表矩阵的迹
变量X 属于positive semidefinite cone(半正定锥?)
$ C, D_{i},A_{i}$ 属于 semidefinite cone(正定锥?)
4.2 形式二
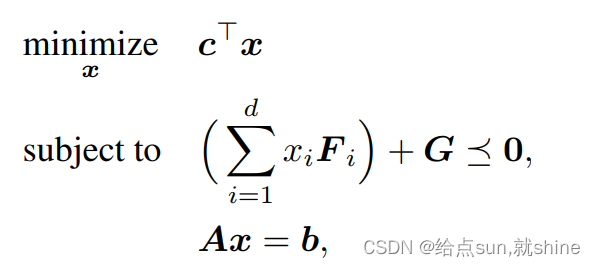
特点:
G
,
F
i
G,F_{i}
G,Fi?属于semidefinite cone(正定锥?)
5.nonlinear programming (NLP,非线性规划)
特点:
目标函数或约束存在非线性函数
例如:
约束中存在非线性函数的例子

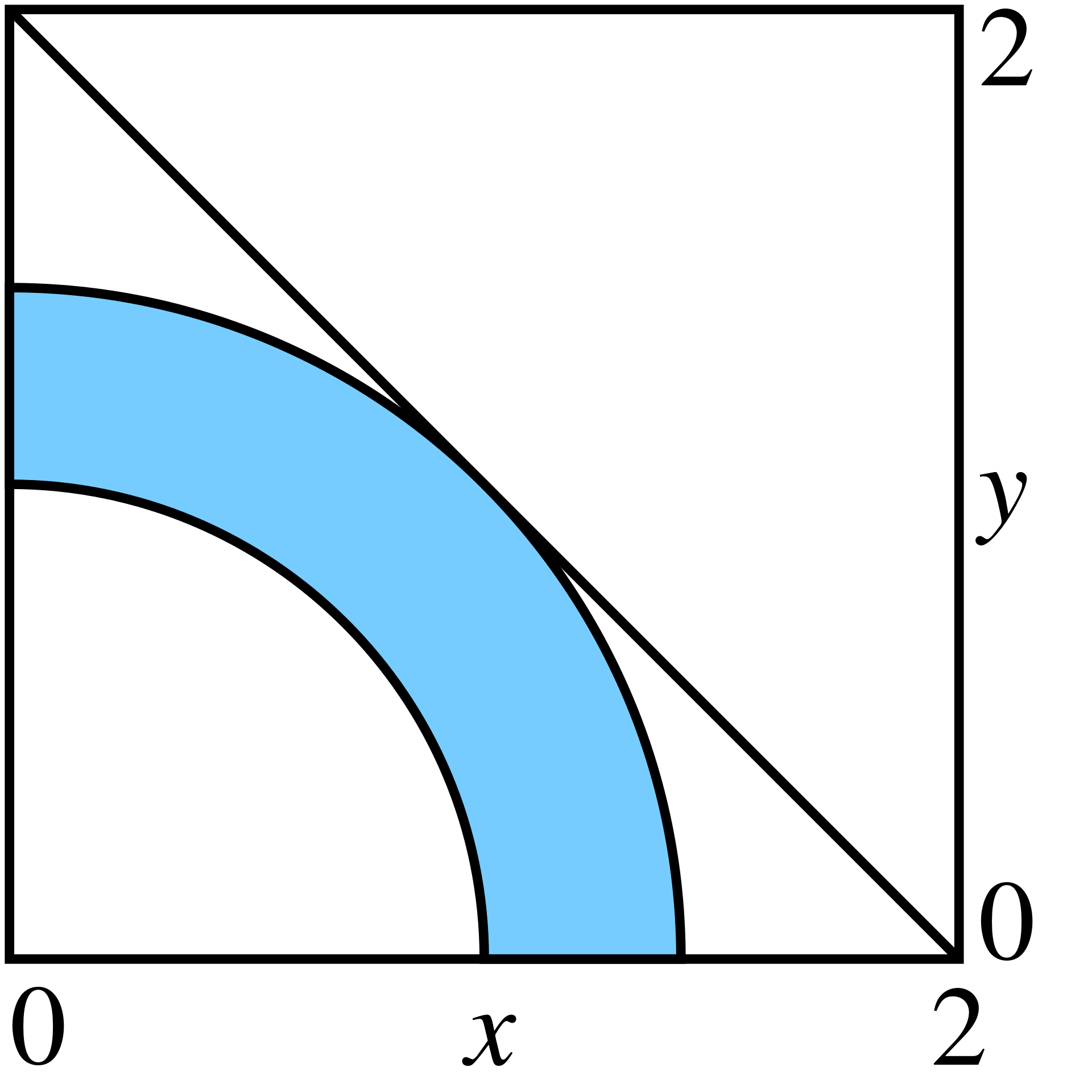
图中蓝色区域为约束的可行域,直线代表目标函数的最佳取值,而直线与可行域的交点即为解X。
6.least squares(LSQ,最小二乘)
问题:求解曲线拟合

对于该问题的一个目标函数定义为:
min
?
∑
i
=
1
m
L
i
2
(
x
)
=
min
?
∑
i
=
1
m
L
i
2
[
y
i
,
f
(
x
i
)
]
=
min
?
∑
i
=
1
m
[
y
i
?
f
(
x
i
)
]
2
\min \sum_{i=1}^m L_i^2(x)=\min \sum_{i=1}^m L_i^2\left[y_i, f(x_i)\right]=\min \sum_{i=1}^m\left[y_i-f(x_i)\right]^2
mini=1∑m?Li2?(x)=mini=1∑m?Li2?[yi?,f(xi?)]=mini=1∑m?[yi??f(xi?)]2
其中
L
i
(
x
)
(
i
=
1
,
2
,
?
?
,
m
)
L_{i}(x)(i = 1,2,\cdots,m)
Li?(x)(i=1,2,?,m)称为残差函数,如果
L
i
(
x
)
(
i
=
1
,
2
,
?
?
,
m
)
L_{i}(x)(i = 1,2,\cdots,m)
Li?(x)(i=1,2,?,m)是
x
x
x的线性函数,则称为线性最小二乘(LLSQ, linear least squares), 否则称为非线性中最小二乘(NLLSQ,nonlinear least squares)。如果线性最小二乘中,除了要尽量曲线拟合外,还有一些应用上的要求,比如一定要经过某个点,那么这种带约束的问题,称之为约束线性最小二乘(constrained linear least squares)。
7.(SQP,序列二次规划)
考虑一个非线性规划问题,但是要求目标函数和约束条件都需要二阶连续可微
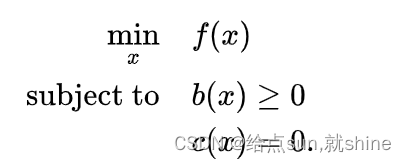
在第k次迭代时,可以通过求解下面SQP子问题为其确定迭代方向
d
k
d_{k}
dk?
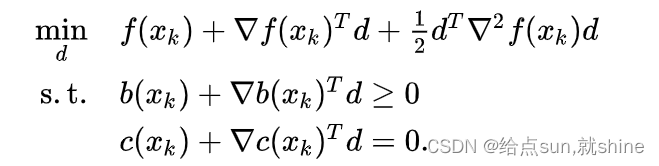
reference:
1.KKT Conditions, First-Order and Second-Order Optimization, and Distributed Optimization: Tutorial and Survey
2.https://baike.baidu.com/item/%E6%9C%80%E5%B0%8F%E4%BA%8C%E4%B9%98%E6%B3%95/2522346?fr=kg_general(最小二乘法)
3.https://en.wikipedia.org/wiki/Sequential_quadratic_programming(SQP)