“假设光归根结底是波,只是给我们以粒子的印象,因为粒子吸收光波的能量是以离散的包的方式。波从源头传播出去像一个越来越大正在膨胀的气泡,到达一个原子时,气泡破裂,波坍缩并把所有的能量集中在一个地方,像大海里的波浪破碎在拱形的海湾。到那时,气泡会变得巨大,坍缩会突然大面积地发生。远处的气泡如何能知道它们应该马上停止向外传播?一定存在某些神秘的非定域效应在暗中运行。
假设光归根结底是粒子的。光有时看起来像波,那只是因为粒子能协同合作像波一样运动,好像体育场看台上的观众形成的波。光的粒子独立运动可以解释光谱中的短波一边,但解释不了长波一边。在长波那边,粒子不可能互相独立,仍需要外在的影响使得它们协同扭动。”
华盛顿大学物理学家约翰·克雷默称之为“气泡佯谬”
前述实验表明在保持等位点数值差一致的前提下,神经网络的迭代次数是相同的,和图片的尺寸无关。
( A , B )---(x*x)*30*2---( 1, 0 )( 0, 1 )
当x=3,移位距离s=5
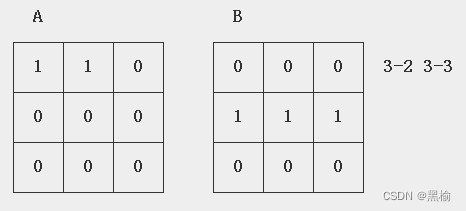
当x=5,移位距离s=5
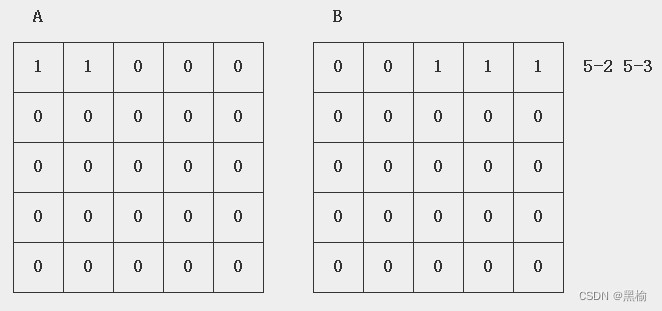
x分别等于3,5,7,9,11,13,15,17,19,21.时的迭代次数数据
| 3-2 3-3 | 5-2 5-3 | 7-2 7-3 | 9-2 9-3 | 11-2 11-3 | 13-2 13-3 | 15-2 15-3 | 17-2 17-3 | 19-2 19-3 | 21-2 21-3 | |
| δ | 迭代次数n | 迭代次数n | 迭代次数n | 迭代次数n | 迭代次数n | 迭代次数n | 迭代次数n | 迭代次数n | 迭代次数n | 迭代次数n |
| 0.01 | 1319.02513 | 1321.81407 | 1322.60804 | 1318.39698 | 1320.22111 | 1322.34673 | 1321.88945 | 1316.61307 | 1319.92462 | 1320.67337 |
| 0.001 | 7492.84422 | 7454.93467 | 7455.13065 | 7471.90955 | 7461.04523 | 7468.8593 | 7432.21608 | 7450.86935 | 7479.99497 | 7482.46734 |
| 9E-4 | 8142.66834 | 8121.11055 | 8157.65327 | 8123.62814 | 8138.32161 | 8130.73367 | 8142.19095 | 8159.40201 | 8138.29146 | 8163.03518 |
| 8E-4 | 9007.56784 | 8993.04523 | 8993.77889 | 9004.40201 | 9040.40201 | 9014.56281 | 9026.45226 | 8981.46734 | 9041.63819 | 9013.11055 |
| 7E-4 | 10082.0503 | 10079.2663 | 10082.5678 | 10120.3668 | 10094.206 | 10120.9648 | 10131.7688 | 10134.8693 | 10069.1759 | 10098.608 |
| s | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
所有可观察的力学变量都是实力学变量,比如假设被分类的两个矩阵A,B是一对共轭波函数,而我们要观察的力学变量是迭代次数。而迭代次数与图片的尺寸无关,这就表明A中的两个点只要不与B中的3个点位置重合,可以在空间中的任何地方,也可以在任何大的空间之中。
所以有理由认为如果A和B是两个无限大的矩阵,他们的迭代次数也是一样的。所以假设波函数无处不在这个观点可以理解为表达了一种空间尺寸的对称性,迭代次数只与差值有关而与空间尺寸无关。所以空间尺寸对这一实验结果没有任何约束,可以任意大。
所谓波粒二象性似乎就是两种对物质世界的分类方法,按照形态分类物质看起来像波,如果按照元素分类法物质又像序数的点。所以波粒二象性表达的或许就是我们确实可以从形态和元素两个不同的角度对物质世界进行分类。
而之所以存在气泡佯谬是因为我们认为所谓的波其实也是由序数的点构成的,也就是认为元素分类法决定了形态分类法,因而形态和序数可以在同一个层面上去考虑,也就有了变换的问题。
但如果元素分类法和形态分类法是平行的,形态本身有其内在的固有特征功能不能仅仅由序数去描述,不能仅仅基于序数逻辑去重构形态,也不能仅仅基于形态逻辑去表达序数,则两种状态就无法相互转换,也就不存在气泡佯谬。比如是否存在一个数字串与一个正方形严格一一对应,或者是否存在一系列形态与序数序列严格一一对应。
那又如何解释同一件事可以同时从波和粒子的两个角度去认识,得到的结论却是一样的。或许这只表明形态表象和序数表象是有重合的,而其重合的部分兼优形态特征也有序数特征,